Sign of a Potential Difference
Claimed by Junzhe Ruan(Fall 2018)
This article discusses the sign of potential difference, and how to determine the sign in different situations involving a particle and an electric field.
Introduction
From previous sections, we know that the change in potential energy is equal to the charge multiplied by the change in potential difference(δU = q * δV). From Conservation of Energy(δV + δK = 0), the loss of kinetic energy must result in an increase in potential energy and vice versa in one same system. In another word, the change in the potential difference and kinetic energy can be positive or negative. For instance, when one object decreases its speed, its kinetic energy decreases. (δK < 0) Due to the conservation of energy, we can get δV > 0. However, we are mainly discussing the change of potential in an electrical system as shown below:
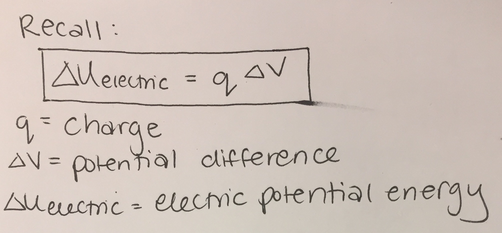
As seen from the equation above, two factors can affect the sign of potential energy. First, the charge of the particle being observed can be positive or negative (proton vs. electron). Second, and the topic of this page, the sign of the potential difference can also determine if a particle is gaining or losing potential energy.
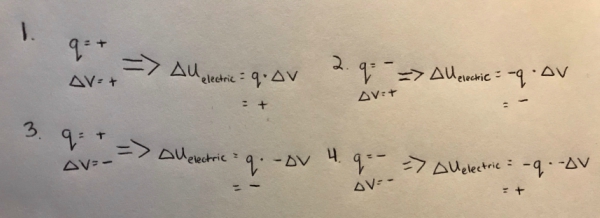
Direction of Path vs. Direction of Electric Field
From the equation relating potential difference with electric field and motion, we can see that the sign of the potential difference is dependent on the direction of both the electric field and displacement vectors, as shown below.
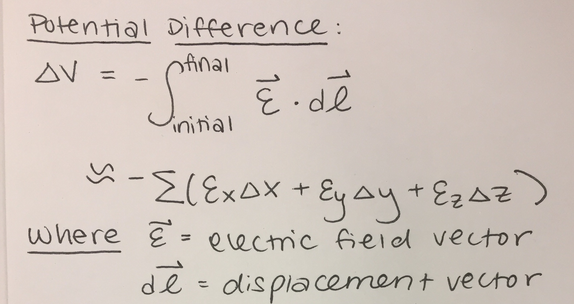
Consistent with the previous convention, the delta symbol (δ) indicates "final - initial." We will use this same notation in showing the direction of the path. For example δ V = Vb - Va ---> signifies the potential difference between location B (final) and location A (initial).
For this equation, note that the result of the cross product between the electric field and displacement is negated before finding the potential difference. Furthermore, it is important to note that the electric field and displacement vectors are multiplied by the dot product. A · B = A * B * cosθ Due to this formula, we will analyze 3 different scenarios: path in the direction of the electric field(θ = 0°), path in the opposite direction of the electric field(θ = 180°), and the path moving perpendicular to the direction of the electric field(θ = 90°).
Quick Review of Delta symbol
In the equation for the potential difference, we see a Delta for the path, also written as dL sometimes. This delta means a change in the path as taken from two different reference points. These reference points are known as initial and final or sometimes source and observation location. To properly calculate a delta or change, you must take the final and subtract the initial from it. More simply, Delta is Final-Initial. In doing problems with electrical field or magnetic field involving potential difference, the first step we usually do is to calculate r = pos_final - pos_initial. Then use it in several advanced formula:
Below are some practice problems to understand what dL would be.
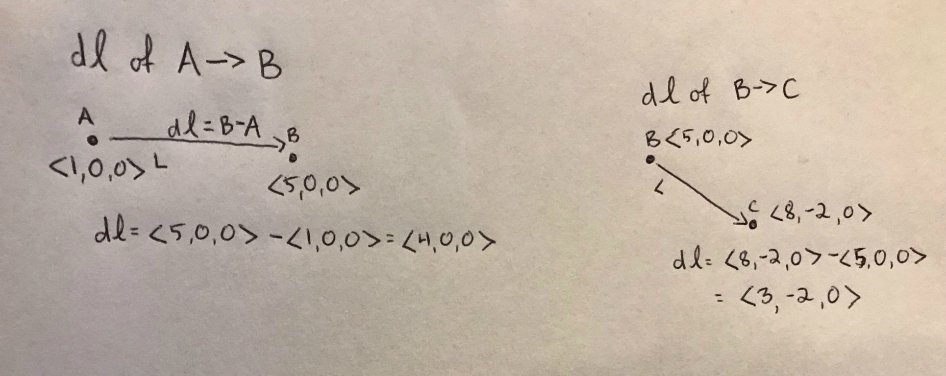
As seen from the problems, direction can differ in the x, y, and z dimensions, but as long as you remember Delta = Final-Initial or Delta = Observation-Source, you will always get the location right! It is important to understand the dimensions of dL as we move forward with determining what the sign of potential difference is.
Sign of Potential Difference

For the last scenario, it will be critical to have a strong understanding of the dot product and how to calculate it. In a mathematical way, A·B = A*B*cos θ where θ is the angle between vector A and B. If A and B are in the same direction, θ = 0, cos θ = 1, then A·B = A*B. If A and B are in opposite direction, θ = 180, cos θ = -1, then A·B = -A*B. Last but not least, if A and B are perpendicular to each other, θ = 90, cos θ = 0, then A·B = 0. This means that when finding the dot product of two perpendicular vectors, the result will be zero.
To better understand this, imagine the electric field between two very long capacitor plates. The electric field points from one plate to the other, let's say in the +x direction. If you wanted to move a charge at any location between the plates in either the +y or -y direction, your displacement vector would point in one of these directions. Whether you moved the particle +y or -y direction, the dot product of the electric field and displacement, and therefore the potential difference, will be zero.
Real Life Example to Explain Sign of Potential Difference
Imagine you are swimming in a stream. The energy the swimmer uses or does not use in this system will represent potential difference. If a swimmer is going along the stream then comes upon a current that starts to push him forward, he does not need to keep stroking in the water as the current can just carry him from one location to the other. This is a great representation of potential difference. Imagine the current in the swimming example is an electric field and that there are two set locations for the swimmer to go from and to. If the current and the change in location (final-initial) are in the same direction, then the swimmer had to use less energy swimming. This drop in energy can represent the negative potential difference. Both the current (electric field) and change in location (dL) were in the same direction, so the swimmer let the current carry him rather than exert energy himself (negative potential difference).
Now imagine if the same swimmer decided to test his endurance skills and swim upstream instead, or against the current. Now, the theoretical electrical field and change in location (dL) are opposing each other. This now means that the swimmer must exert a lot of his own energy to get from point A to B while opposing the current pushing against him. Looking at the energy in the scenario, the swimmer now has to provide a change in energy that he, himself, makes, so the potential difference would be positive. In reference to the swimmer, he is providing the energy as opposed to letting the current provide it like in the previous example. This shows that opposite directions mean a positive potential difference.
Finally, imagine if you were swimming perpendicular to the current. Now, the dL and electrical field equivalents are running perpendicular to each other. The swimmer does not have to exert any more or less energy to get from point A to B because the current is not in the same dimension as the initial and final locations. This shows why potential difference = 0 when the dot product of Electric Field and dL is carried out.
Another real-life example is to imagine you are carrying a ball and prepare to throw it from the building. If you go downstairs (the same direction as the gravity.), the potential of the ball you carry is decreasing, because when you throw it, it takes a shorter time to reach the ground. Thus this movement has a negative potential difference. So on so forth, if you go upstairs (opposite direction as the gravity), the potential increases because it takes a longer time for the ball to reach the ground and when it reaches it, it has a larger energy. Due to δpotential = final potential - initial potential, the potential difference is positive. From this example, again, we can conclude that "opposite directions" means positive potential difference and same direction means negative potential difference. It should be the same on gravity potential field and electrical potential field.
Easier Examples
Reminder:
Path going in direction of E Field ------> Potential is decreasing
Path going opposite to E Field -------> Potential is increasing
Path perpendicular to E Field --------> Potential does not change / =0
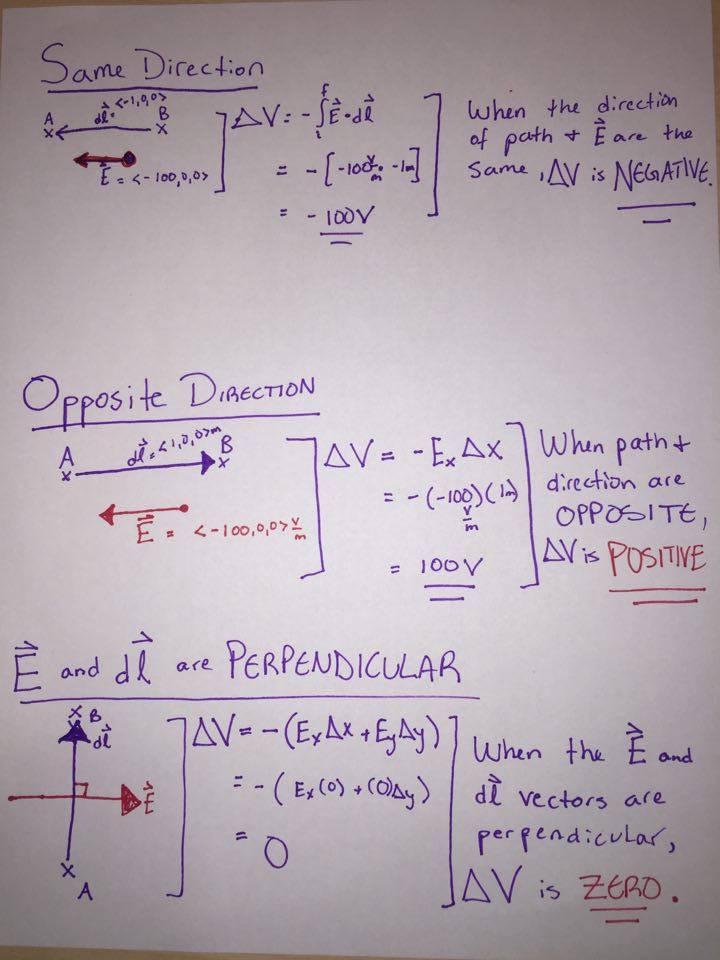
To better understand this, we could imagine in this way: E field makes positively charged particle to move along its path, as a positive particle, as it goes in direction of E Field, its potential of moving decrease. In another word, after the E field use its function (move the particle in a particular direction), the potential of it moving the particle decrease. And vice versa.
Harder Example

Let's go through this problem step by step.
a) How would you get the dL of the path going from B to A? Well, recall that dL = final-initial, so you must do: location of A - location of B:
<-2.5, 1, 0> - <4, -2.4, 0> = <-6.5, 3.4, 0> meters
Now you have the dL or the vector from B to A.
b) Now, how do you get the potential difference if a particle is moving from B to A given the electric field and the dL from part a)? You know it is just the dot product of Electric Field and dL:
∆V = -(E · dL) = -((-6.5 x -450) + (3.4 x 300) + (0 x 0)) = -(2925 + 1020 + 0) = -3945 volts
c) Now that you know the potential difference, ∆V, how would you calculate the potential energy of the system if the particle was a proton? Well, now you just multiple the ∆V by the q, or charge of the proton.
∆U = ∆V x q = -3945 x 1.6 e-19 = -6.3 e-16 joules
d) Now, how would you calculate the potential energy of the system if the particle was an electron instead of a proton? Well, you know that the only difference between this and part c) is that the charge is now negative to account for the electron but the same number.
∆U = ∆V x q = -3945 x -1.6 e-19 = 6.3 e-16 joules
These questions are very simple as long as you think methodically about what you are doing and always keep in mind two very important things:
1) What is the initial and final for the particle's path? Again, dL is always final-initial!
2) Is the particle a proton or an electron? The number for charge will be the same but the sign will change dependent on which one it is. Sign is important!
Summary
Determining potential difference and its sign is very simple if you remember these ideas:
1. Electric field and displacement vectors can be in all three dimensions, but the dot product makes the sum of all these dimensions the answer.
2. dL will ALWAYS be final-initial!
3. Never forget the negative in the ∆V = -(E · dL) equation. This is probably the easiest way to mess up a problem because it is hardest to remember. Just recall the swimmer example from above if you get confused!
When determining the sign of the potential difference, there will be 3 different scenarios that will determine whether the sign of the potential difference is positive, negative, or zero. Pay close attention to notation when considering the change in a quantity (potential, displacement, etc..) in order to avoid confusing the wrong sign. Attention to detail when find the sign of potential difference will make solving the more difficult problems at the end of the chapter a little easier. The following summary of the 3 scenarios is extremely helpful:
