Scattering: Collisions in 2D and 3D
Edwin Zhao - Spring 17
The Main Idea
Scattering (Rutherford Scattering) is a type of experiment that is used to study the structure and behavior of atoms, nuclei, and other small particles. This allows us to understand small particles on a greater level.
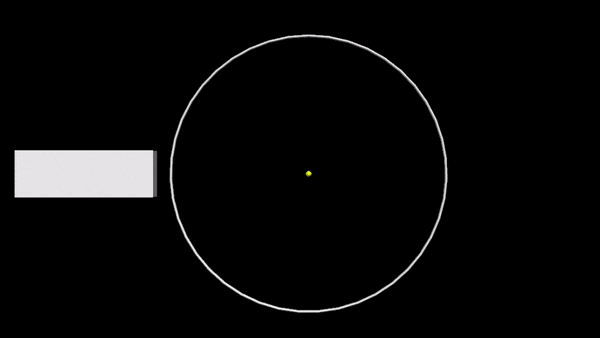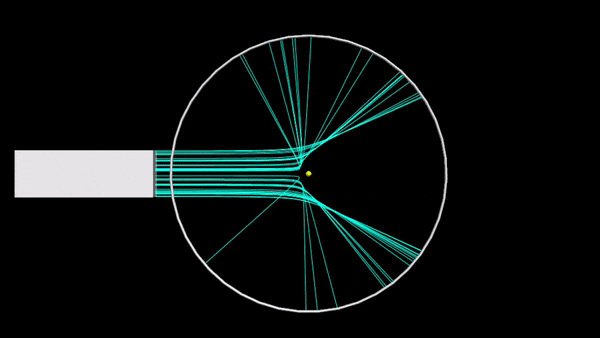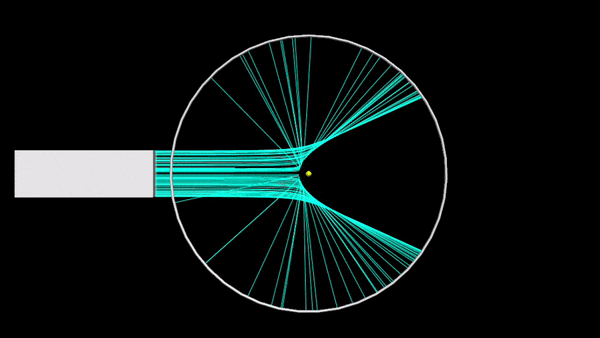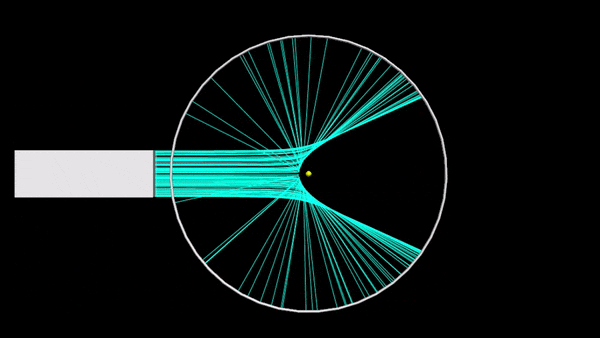
Unlike normal collisions, atomic and nuclear collisions are far too small to observe the curving trajectories of the interacting particles. The only things that can be noticed are the initial and final states of the interaction. Therefore, the method of observing scattering consisted of alpha particles from a radioactive source striking a thin gold foil. Since it is only a very small number of atoms are observed to scatter after contact with the gold, it can be determined that the majority of the material is positively charged, and when the alpha particle (positive) travels through and approaches close enough to the nucleus, it will be repelled and then "scatter" by a large angle.
By finding the back-scattering, it shows that atoms are arranged tightly together. Scattering experiments are useful in the world of collisions to be able to study the minute details in the structure of atoms, nuclei, and other tiny particles as they interact with one another.
After collision with the gold nucleus, the alpha particle gets deflected some angle θ. The gold nucleus recoils at some angle Φ. It is important to pick optimal time frames ("before" early enough and "after" late enough) so that the two particles are far enough away from each other to minimize their electric potential energies. The speeds in this approach are small in comparison to the speed of light.
The case of Rutherford scattering of alpha particles with gold nuclei is an example of elastic scattering because the initial and final velocities and energies are the same.
Impact Parameters
An impact parameter is the distance between centers of the colliding objects perpendicular to the incoming velocity. Impact parameter is often denoted by the variable b.
A head-on collision has an impact parameter of zero, and with equal masses fully transfers the momentum- such as with Newton's Cradle. As the impact parameter gets smaller the collision has a larger effect, and an even large deflection angle (scattering).
A Mathematical Model
[math]\displaystyle{ p_{xi} = p_{xf} }[/math]
[math]\displaystyle{ p_1 = p_3 cosθ + p_4 cosΦ }[/math]
[math]\displaystyle{ p_{yi} = p_{yf} }[/math]
[math]\displaystyle{ 0 = p_3 cos(90° - θ) + p_4 cos(90° + Φ) }[/math]
[math]\displaystyle{ K_f = K_i }[/math]
[math]\displaystyle{ \frac{p^2_1}{2m} = \frac{p^2_3}{2m} + \frac{p^2_4}{2M} }[/math]
Where [math]\displaystyle{ p_1, p_3, }[/math] and [math]\displaystyle{ p_4 }[/math] are all magnitudes of the momenta. It can be remembered that the gold nucleus is initially at rest.
The directions of cosine are used to express vector components to the x-axis.
ex. Final momentum of gold nucleus [math]\displaystyle{ {= \vec{p_4} = |\vec{p_4}| \lt cosΦ, cos(90° + Φ), 0\gt } }[/math]
A Computational Model
Rutherford's scattering
A simulation that shows the difference between Rutherford's model and the plum pudding model.
Examples
Simple
Question
Imagine you recreate Rutherford's experiment. You find, like he did, that a very small percentage of alpha particles are deflected at angles over 90 degrees. Why is this?
Answer
Alpha particles are deflected because their positive charge is repulsed by the positive charge of the nucleus. The repulsive force is stronger with smaller distance between the alpha particle and nucleus by principles of electromagnetism. Therefore, the closer the alpha particle is shot to the center of the nucleus, the stronger the force on the alpha particles, and the larger the angle of deflection.
Middling
Question
Rutherford found that the fraction of particles scattered at an angle [math]\displaystyle{ θ }[/math] or greater can be modeled by the equation [math]\displaystyle{ F_{θ} ≈ e^{(−θ/θ^2_m)} }[/math]. At what angle would Rutherford have found a fraction of [math]\displaystyle{ 10^{45} }[/math] particles to be at that angle or greater than? ([math]\displaystyle{ θ_m ≈ 1 }[/math] for a gold leaf foil)
Answer
Using the formula [math]\displaystyle{ F_{θ} ≈ e^{(−θ/θ^2_m)} }[/math], we can rearrange to solve for θ by taking the log of both sides:
[math]\displaystyle{ log(F_{θ}) = −θ/θ^2_m }[/math]
Then, we can multiple by [math]\displaystyle{ -θ^2_m }[/math] to find:
[math]\displaystyle{ θ = −(θ^2_m)log(F_{θ}) }[/math]
Plugging in the given information, [math]\displaystyle{ θ = −(1^2)log(10^{45}) = 45 }[/math]. Therefore, a fraction of [math]\displaystyle{ 10^{45} }[/math] particles are scattered at about an angle of 45 degrees or greater.
Difficult
Question
Imagine you are looking at a scattering simulation. Using the same formula [math]\displaystyle{ F_{θ} ≈ e^{(−θ/θ^2_m)} }[/math] as the previous question, at what deflection angle would you have to look at such that only 1 in a million particles are scattered at that angle?
Answer
1 in a million would correspond to a [math]\displaystyle{ F_{θ} }[/math] of [math]\displaystyle{ \frac{1}{1000000} = .000001 }[/math]
Using the formula [math]\displaystyle{ F_{θ} ≈ e^{(−θ/θ^2_m)} }[/math], we can rearrange to solve for θ by taking the log of both sides:
[math]\displaystyle{ log(F_{θ}) = −θ/θ^2_m }[/math]
Then, we can multiple by [math]\displaystyle{ -θ^2_m }[/math] to find:
[math]\displaystyle{ θ = −(θ^2_m)log(F_{θ}) }[/math]
Plugging in the given information, [math]\displaystyle{ θ = −(1^2)log(.000001) = 6 }[/math]. Only 1 in a million particles are scattered at an angle of 6 degrees or greater.
Connectedness
Scattering is most closely connected to the Rutherford Experiment, which has large implications in chemistry. This experiment led to the discovery of the nucleus and acted as a vital stepping stone to other discoveries in the structure of atoms and characteristics of periodic elements. This increased awareness of the parts that make up atoms also led to advances in medicine and nuclear physics.
History
In 1871 Lord Rayleigh published a paper on scattering. Rayleigh scattering is the dispersion of electromagnetic radiation by particles that have a minute radius less than approximately 1/10 the wavelength. It laid the foundation to research on scattering and information we have today.
In Ernest Rutherford's laboratory with Hans Geiger and Ernest Marsden, they experimented with tests of scattering alpha particles with thin metal foils. In 1909, Geiger and Marsden discovered scattering through their gold foil experiments. From this, they discovered that some alpha particles scattered at angles greater than 90°.
See also
Further reading
Matter and Interactions, Volume I: Modern Mechanics, 4th Edition. (Chapter 10.6)
External links
References
Chabay, Ruth W., Bruce Sherwood. Matter and Interactions, Volume I: Modern Mechanics, 4th Edition. Wiley, 19/2014.
“Rutherford Scattering.” MIT OpenCourseWare, MIT Department of Physics , ocw.mit.edu/courses/physics/8-13-14-experimental-physics-i-ii-junior-lab-fall-2016-spring-2017/experiments/rutherford-scattering/MIT8_13-14F16-S17exp15.pdf.