Rotational Kinematics
Claimed by Allen Ayala (Fall 2019)
The Main Idea
Rotational Motion (also known as curvilinear motion), in contrast to linear ( also known as rectilinear) motion, involves motion of objects where the angular orientation of an object changes over time (For this reason, it is common practice to use polar coordinates when analyzing any object undergoing rotational motion). Rotational quantities (also called "angular quantities") describe the angular components of an object's motion.
When working in the context of rotational kinematics, there is usually a defined point of rotation for which motion is analyzed. Examples of this include rotating about an object's center of mass (as in a wheel spinning on an axle) and a planet about a star.

A Mathematical Model
Similar to linear motion, angular quantities can be described by a series of differential equations which relate the rate of change of a given quantity to some other aspect of rotational motion. These equations are listed below:
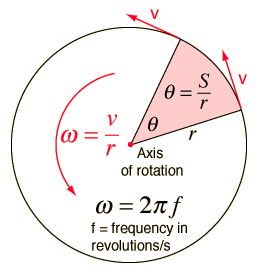
- [math]\displaystyle{ \boldsymbol{\omega} = \frac{d\boldsymbol{\theta}}{dt} }[/math]
- [math]\displaystyle{ \boldsymbol{{\alpha}} = \frac{d\boldsymbol{\omega}}{dt} }[/math]
- [math]\displaystyle{ \boldsymbol{{\alpha}} = \frac{{d}^{2}\boldsymbol{\theta}}{{dt}^{2}} }[/math]
Here [math]\displaystyle{ \boldsymbol{\theta} }[/math] represents angular position, [math]\displaystyle{ \boldsymbol{\omega} }[/math] represents angular velocity, and [math]\displaystyle{ \boldsymbol{\alpha} }[/math] represents angular acceleration. One can also approximate the rotational motion of an object by using the discrete time equations of motion, as listed below:
- [math]\displaystyle{ \boldsymbol{\omega} = \frac{\Delta\boldsymbol{\theta}}{{\Delta}t} }[/math]
- [math]\displaystyle{ \boldsymbol{\alpha} = \frac{\Delta\boldsymbol{\omega}}{{\Delta}t} }[/math]
Objects undergoing rotational motion, just like objects undergoing linear motion, can be analyzed using kinematics, and in principle, by using the relationships above, it is possible to solve for every aspect of an object's rotational motion. However, depending upon the complexity of the motion, this task may prove extremely difficult, so, more often than not special cases are considered, such as "rotation about a fixed axis" or "uniform circular motion". While these special cases may make simplifications about certain aspects of the object's motion, they still make use of the same equations of motion, and thus are still rotational kinematics problems. A special case of particular importance however is the case in which an object in undergoing uniform angular acceleration. In this case, it is possible to derive equations analogous to the Uniformly accelerated motion equations from linear kinematics. These equations are listed below:
- [math]\displaystyle{ \boldsymbol{\omega} = {\omega}_{0} + \boldsymbol{\alpha}t }[/math]
- [math]\displaystyle{ \boldsymbol{\theta} = \frac{1}{2}\boldsymbol{\alpha}{t}^{2} + {\omega}_{0}t + {\theta}_{0} }[/math]
- [math]\displaystyle{ \boldsymbol{{\omega}}^{2} = {{\omega}_{0}}^{2} + 2\boldsymbol{\alpha}(\boldsymbol{\theta} - {\theta}_{0}) }[/math]
Similarities to linear motion
For those who have already studied linear kinematics, it is fairly easy to identify each linear variable's rotational counterpart in the rotational equations that we have seen. Students who may struggle to remember the equations regarding rotational motion should recognize that the rotational kinematics equations are analogous to previously studied linear equations. To observe this connection, we must identify each linear variable's rotational counterpart :
- Rotational [math]\displaystyle{ \Longleftrightarrow }[/math] Linear
- [math]\displaystyle{ \boldsymbol{\theta} \Longleftrightarrow \boldsymbol{x} }[/math]
- [math]\displaystyle{ \boldsymbol{\omega}\Longleftrightarrow \boldsymbol{v} }[/math]
- [math]\displaystyle{ \boldsymbol{\alpha}\Longleftrightarrow\boldsymbol{a} }[/math]
It should be fairly apparent why each of these variables corresponds with their respective counterparts. For [math]\displaystyle{ \boldsymbol{\theta} }[/math], the angle that defines an object's orientation is analogous to an object's position, [math]\displaystyle{ \boldsymbol{x} }[/math]. Once this relation is recognized, the connection between the other kinematic variables should be obvious.
After seeing the connection between linear and rotational kinematic variables, it can be observed their kinematic equations are virtually identical:
- Rotational [math]\displaystyle{ \Longleftrightarrow }[/math] Linear
- [math]\displaystyle{ \boldsymbol{\omega} = \frac{d\boldsymbol{\theta}}{dt} }[/math] [math]\displaystyle{ \Longleftrightarrow \boldsymbol{v} = \frac{d\boldsymbol{x}}{dt} }[/math]
- [math]\displaystyle{ \boldsymbol{{\alpha}} = \frac{d\boldsymbol{\omega}}{dt} }[/math] [math]\displaystyle{ \Longleftrightarrow \boldsymbol{a} = \frac{d\boldsymbol{v}}{dt} }[/math]
- [math]\displaystyle{ \boldsymbol{{\alpha}} = \frac{{d}^{2}\boldsymbol{\omega}}{{dt}^{2}} }[/math] [math]\displaystyle{ \Longleftrightarrow \boldsymbol{a} = \frac{{d}^{2}\boldsymbol{x}}{dt} }[/math]
- [math]\displaystyle{ \boldsymbol{\omega} = {\omega}_{0} + \boldsymbol{\alpha}t }[/math] [math]\displaystyle{ \Longleftrightarrow \boldsymbol{v} = {v}_{0} + \boldsymbol{a}t }[/math]
- [math]\displaystyle{ \boldsymbol{\theta} = \frac{1}{2}\boldsymbol{\alpha}{t}^{2} + {\omega}_{0}t + {\theta}_{0} }[/math] [math]\displaystyle{ \Longleftrightarrow \boldsymbol{x} = \frac{1}{2}\boldsymbol{a}{t}^{2} + {v}_{0}t + {x}_{0} }[/math]
- [math]\displaystyle{ \boldsymbol{{\omega}}^{2} = {{\omega}_{0}}^{2} + 2\boldsymbol{\alpha}(\boldsymbol{\theta} - {\theta}_{0}) }[/math] [math]\displaystyle{ \Longleftrightarrow \boldsymbol{{x}}^{2} = {{x}_{0}}^{2} + 2\boldsymbol{a}(\boldsymbol{x} - {x}_{0}) }[/math]
Examples
Simple
A simple example and application of the concept of rotation is the earth's rotation on it's axis. Given that the Earth completes one rotation every 24 hours, what is it's angular velocity in radians per second?
Given that we know the amount of time it takes for the Earth to complete one revolution, and one revolution is simply [math]\displaystyle{ 2\pi }[/math] radians, we can state that:
- [math]\displaystyle{ \Delta\boldsymbol{\theta} = {2\pi}\: rad }[/math]
- [math]\displaystyle{ {\Delta}t = {24}\: hr }[/math]
Since we are solving for [math]\displaystyle{ \boldsymbol{\omega} }[/math] and we have [math]\displaystyle{ \Delta\boldsymbol{\theta} }[/math] and [math]\displaystyle{ {\Delta}t }[/math], we can use the discrete time equation for angular velocity:
- [math]\displaystyle{ \boldsymbol{{\omega}} = \frac{\Delta\boldsymbol{\theta}}{\Delta t} }[/math]
Substituting in our values, we obtain:
- [math]\displaystyle{ \boldsymbol{{\omega}} = \frac{2\pi}{24}\frac{rad}{hr} }[/math]
We can then simply convert to radians per second:
- [math]\displaystyle{ \boldsymbol{{\omega}} = {\frac{2\pi}{24}\frac{rad}{hr}}\times{\frac{1}{3600}\frac{hr}{s}} }[/math]
- [math]\displaystyle{ \boldsymbol{{w}} = \frac{\pi}{43200}\frac{rad}{s} }[/math]
Medium
A torque is exerted on a disk initially at rest, causing the disk to undergo constant angular acceleration for 20 s. During this time, the disk completes 20 full rotations. What was the angular acceleration of the disk during this time?
To begin, this problem, we can start by recognizing that we are given:
- [math]\displaystyle{ {\omega}_{0} = 0\: \frac{rad}{s} }[/math]
- [math]\displaystyle{ \theta = 40\pi\: rad }[/math]
- [math]\displaystyle{ {\Delta}t = 20\: s }[/math]
We also are given the information that the angular acceleration is constant during this period of time, so we can use the Uniform angular acceleration equations. In this case, we are given [math]\displaystyle{ {\omega}_{0} }[/math], [math]\displaystyle{ \theta }[/math], and [math]\displaystyle{ {\Delta}t }[/math], and we are attempting to solve for [math]\displaystyle{ \alpha }[/math], so it is best to use:
- [math]\displaystyle{ \theta = \frac{1}{2}\boldsymbol{\alpha}{t}^{2} + {\omega}_{0}t + {\theta}_{0} }[/math]
- [math]\displaystyle{ {\theta}_{0} = 0 }[/math]
- [math]\displaystyle{ 40\pi = \frac{1}{2}\boldsymbol{\alpha}{20}^{2} }[/math]
- [math]\displaystyle{ \boldsymbol{\alpha} = \frac{80\pi}{400}\frac{rad}{s} }[/math]
Difficult
Given an angular acceleration modeled by:
- [math]\displaystyle{ \alpha = K{e}^{-{\beta}t} }[/math]
Where [math]\displaystyle{ K }[/math], and [math]\displaystyle{ \beta }[/math] are both constants.
Find the equations which model the angular velocity and angular displacement as a function of time.
In this problem, as we have an angular acceleration which varies as a function of time, it is important to note that our uniform angular accelerated motion equations are invalid as they require acceleration be constant. Therefore, we must use the basic relationships between [math]\displaystyle{ \omega }[/math], [math]\displaystyle{ \theta }[/math], and [math]\displaystyle{ \alpha }[/math]:
- [math]\displaystyle{ \alpha = \frac{d\omega}{dt} }[/math]
- [math]\displaystyle{ \alpha = \frac{{d}^{2}\omega}{{dt}^{2}} }[/math]
Therefore, beginning with angular velocity, we have:
- [math]\displaystyle{ K{e}^{-{\beta}t} = \frac{d\boldsymbol{\omega}}{dt} }[/math]
- [math]\displaystyle{ {\int}K{e}^{-{\beta}t}dt = {\int}\frac{d\boldsymbol{\omega}}{dt}dt }[/math]
- [math]\displaystyle{ {\int}K{e}^{-{\beta}t}dt = \boldsymbol{\omega} }[/math]
- [math]\displaystyle{ K{\int}{e}^{-{\beta}t}dt = \boldsymbol{\omega} }[/math]
This integral can then be solved via u substitution (for more information on solving Integrals, you can click on the following link: U sub). However, here we will simply give the solution to the integral:
- [math]\displaystyle{ \omega = \frac{-K}{\beta}{e}^{-{\beta}t} }[/math]
Next, we must solve for the angular displacement function. To do this, we simply integrate the angular velocity function:
- [math]\displaystyle{ \omega = \frac{d\boldsymbol{\theta}}{dt} }[/math]
- [math]\displaystyle{ \frac{-K}{\beta}{e}^{-{\beta}t} = \frac{d\boldsymbol{\theta}}{dt} }[/math]
- [math]\displaystyle{ \int\frac{-K}{\beta}{e}^{-{\beta}t}{dt} = \int\frac{d\boldsymbol{\theta}}{dt}dt }[/math]
- [math]\displaystyle{ \int\frac{-K}{\beta}{e}^{-{\beta}t}{dt} = \boldsymbol{\theta} }[/math]
Finally, we arrive at:
- [math]\displaystyle{ \boldsymbol{\theta} = \frac{K}{{\beta}^{2}}{e}^{-{\beta}t} }[/math]
Connectedness
Rotation is an extremely important aspect of dynamics (the study of moving objects). Every object can experience rotational motion, thus it is crucial that we understand the tools to analyze this type of motion. Such an example can be found in biomechanics, where rotation relates to several important body parts such as the shoulder where there are two axis of rotation, the medial-lateral axis and the anterior-posterior axis. A study of the movement of the shoulder helps to treat medical conditions that may affect this area.
History
The general concept of rotation was well known to those as far back as ancient Egypt. For example, the Egyptians were aware of the fact that when a force was applied to a round object, such as a log, the object would rotate, or roll across the ground. Archimedes also appeared to be aware of a consequence of torque, which he described as "the principle of the lever". He noted in his work that "Magnitudes are in equilibrium at distances reciprocally proportional to their weights" when discussing objects balancing about a pivot.

Beyond this point, the first time angular velocity and rotational inertia were discussed by name and given precise definitions were by Thomas Bradwardine and Jean Buridan, respectively. Buridan was notable in that he was also the first to roughly define the notion of angular momentum, as he noted that the celestial bodies maintained rotational motion around the sky, not due to an external force, but because their own inertia (or impedus as he called it) carried them forward, encountering no external resistance. Or, in his own words:
"it could be said that God, in creating the world, set each celestial orb in motion… and, in setting them in motion, he gave them an impetus capable of keeping them in motion without there being any need of his moving them any more." - Jean Buridan
See also
Although the equations in rotational kinematics are useful tools, they become much more powerful when used alongside the angular momentum (as one could guess this topic is analogous linear momentum). Thus, interested students could expand upon their growing knowledge by going through the following readings:
Within this student wiki:
To learn more about Rotation in a more complete context, please refer to [Torque] or Rigid-Body Objects or [Angular Momentum].
Further reading
Books, Articles or other print media on this topic
https://brilliant.org/wiki/angular-kinematics-problem-solving/
https://courses.lumenlearning.com/physics/chapter/10-2-kinematics-of-rotational-motion/
External links
Some other resources to further understand rotation are the following:
http://www.mathwarehouse.com/transformations/rotations-in-math.php
http://demonstrations.wolfram.com/Understanding3DRotation/
References
[1] Biomechanics, Basic. “It Is Important When Learning about (n.d.): n. pag. Web.
[2] "Angular Velocity and Angular Acceleration." Van Nostrand's Scientific Encyclopedia (2005): n. pag. Web