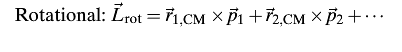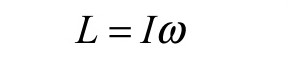Rotational Angular Momentum
Claimed by: Tiffany Zhou
Main Idea
What is Rotational Angular Momentum? In short, rotational angualr momentum is the momentum of an object spinning on its own axis. Therefore if an object does not spin on its own axis, then it does not have a rotational angualr momentum. This page will give you and overall understanding of rotational angular momentum, through a couple practice problems and detailed explanation of rotational angular momentum and its relationship with other physics concept.
Total angualr momentum can be defined as the sum of the translational and rotational angualr momentum. In other words, we can find rotatational angualr momentum without anything more than simple subtration, if we have both the total angular momentum and translational momentum.
In other cases, solving for rotational angular momentum will take more than just subtraction, and require us to use some of the equation listed below.
Mathematical Model
There are two equations that can be used to describe rotational angular momentum. The first one is a generalized form that can be described as the sum of cross products of distance and momentum.
The next equation summarizes rotational angular momentum as the product of inertia and angular velocity.
(The units of rotational angular momentum are kg*m^2/s.
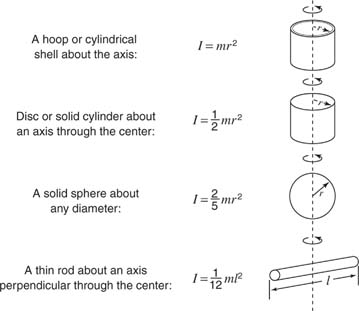
To use the above equation, the following equations may be needed. The first equation is used to calculate the moment inertia. The moment of inertia can be defined as the tendency to resist changes in their state of motion. (The units of inertia are kg*m^2.)
The next equation angular velocity which is the rate of change of angular position of a rotating object. (The units of angular velocity are radians per second).
Rotational angular momentum can be determined if you know the total angular momentum of a system and its translational angular momentum. The relationship is expressed as: [math]\displaystyle{ L_{\text{rot}} = L_{\text{total}} - L_{\text{trans}} }[/math] [math]\displaystyle{ L_{\text{total}} \text{ is the sum of all angular momentum in the system.} \\ }[/math] [math]\displaystyle{ L_{\text{trans}} \text{ is the angular momentum due to the object's linear motion relative to a reference point.} \\ }[/math] [math]\displaystyle{ L_{\text{rot}} \text{ represents the angular momentum due to the object's rotation about its own axis.} }[/math]
Computational Model
You can visualize the concept of rotational angular momentum with this simulation: Check out the simulation here of a spinning figure skater extending arms(the rod is the body balls the arms): Click here to view the simulation
Examples
Listed below are examples of rotational angular momentum problems.
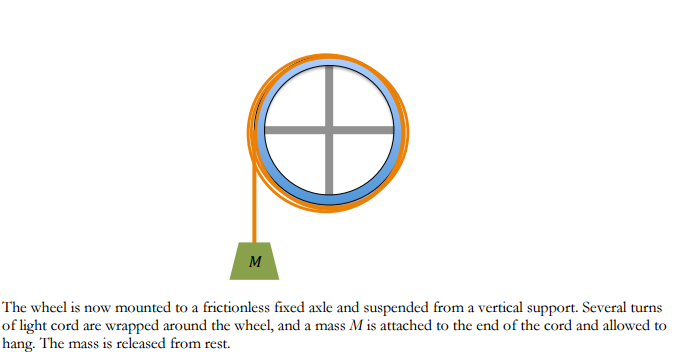
Simple
Below is a conceptual rotational angular momentum problem.
Middling
These rotational angular momentum problems use both the inertia and angular velocity equations.
Example 1
Example 2
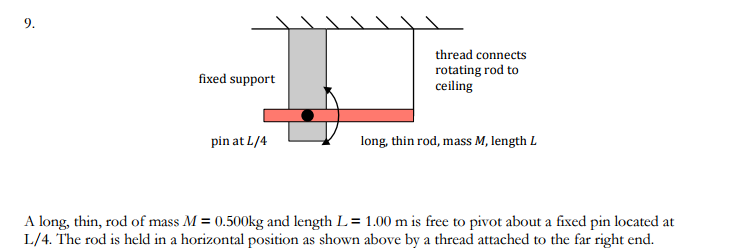
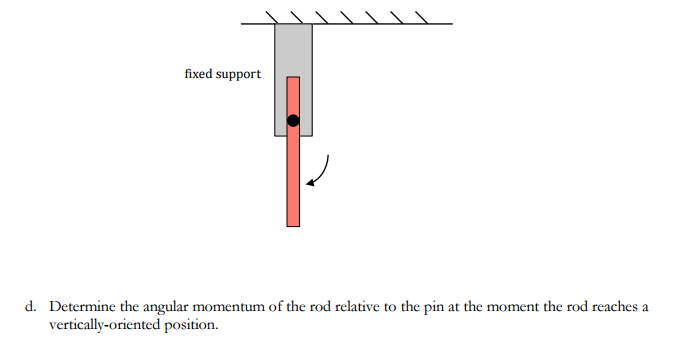
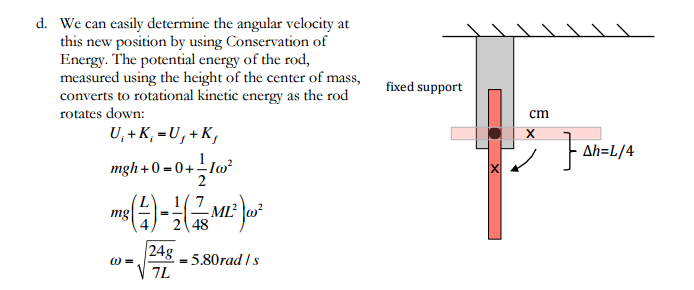
Difficult
Example 1
Example 2
Connectedness
Rotational angular momentum can be applied to every day life. Examples include the earth rotating on its axis, a figure skater, a football spinning as it's being thrown, or even a firing bullet. Anything that rotates on its own axis will have rotational angular momentum.

History
The idea of rotational angular momentum came from Johannes Kepler, a German scientist and astronomer who lived in the late 1500's through the mid 1600's. Kepler believed that planets orbited in an ellipse, but he also needed a rule to describe the change of velocity over time. He discovered a law of areas. This means that as planets orbit the sun, they sweep out in equal areas over equal amounts of time. However, Isaac Newton, a physicist and mathematician who came after Kepler, realized that the area law was part of a larger theory of motion.
Newton's second law particularly covers angular momentum. The second law states that the acceleration is dependent on the net force upon the object and the mass of the object. The vector sum of all torques acting on a particle is equal to the time rate of change of the angular momentum of that particle.
See also
Further reading
Matter and Interactions by Ruth W. Chabay and Bruce A. Sherwood
Elementary Theory of Angular Momentum by M.E. Rose
Angular Momentum in Quantum Mechanics by A.R. Redmonds
External links
http://hyperphysics.phy-astr.gsu.edu/hbase/amom.html https://www.youtube.com/watch?v=MULe4xv3lVk
References
http://www.physicsclassroom.com/class/newtlaws/Lesson-3/Newton-s-Second-Law
https://physics.ucf.edu/~roldan/classes/phy2048-ch10_new.pdf
http://www.physicsclassroom.com/mmedia/circmot/ksl.cfm
http://farside.ph.utexas.edu/teaching/301/lectures/node122.html