Reciprocity

claimed by Anshul Niranjan (Fall 2024)

edited by Laurentino Castro (Spring 2018)

This section covers the top of reciprocity which explains why forces, such as gravitational and electric forces, act upon each other with equal magnitudes. Reciprocity refers to the principle that the force exerted by object A on object B is equal in magnitude and opposite in direction to the force exerted by object B on object A. The reason for this is Newtons Third law which states "for every action, there is an equal and opposite reaction".

This is an example of reciprocity. The book is exerting a contact force on the table and the table is exerting a contact force on the book.

The Main Idea

Reciprocity is the idea that the force object 1 exerts on object 2 is the same as the force object 2 exerts on object 1. This idea comes from Newton's Third Law of Motion, which states that every action has an equal and opposite reaction. For example, if I put my hand on a table, I am exerting a contact force on the table. Because my hand doesn't go straight through the table but instead rests on top of it, the table must also be exerting a force on me that is equivalent to the force I am placing upon it. Though it seems like I am putting in more effort, the forces are the same. This concept applies to various types of forces, including gravitational, electric, and normal forces.

Gravitational Forces: The force between two masses is reciprocal. If object A exerts a gravitational pull on object B, object B exerts an equal and opposite pull on object A. This force depends on the masses and distance between the objects.

Electric Forces: Electric charges also exert reciprocal forces. If one charged object exerts a force on another, the second object exerts an equal and opposite force in return. The magnitude and direction depend on the charges and their separation.

Normal Forces: The normal force, which is the contact force from a surface supporting an object, is rooted in atomic-level electromagnetic interactions. When an object rests on a surface, the surface pushes back with a normal force equal to the object's weight. This is also a reciprocal interaction, with equal forces acting in opposite directions.

At the atomic level, these forces arise from interactions between charged particles in atoms. In contact forces like the normal force, these interactions prevent objects from passing through one another. Reciprocity remains a key principle across all types of forces, helping us understand the fundamental behaviors of the physical world.

Newton's 3rd law implies that all forces come in pairs. The two forces are called "action" and "reaction" pairs. When forces are in these pairs, the magnitude of the two forces equal each other. However, in vector form, the two forces would be in opposite directions of each other, so one force would have a negative sign on it. This applies to both the gravitational and electric forces. Contact forces that we observe (such as the normal force) are actually due to electrical forces at the atomic level.

Because these forces are equal, so are the changes in momentum of the objects the forces are acting upon (remember, [math]\displaystyle{ |\vec{\mathbf{F}}|=|\frac{d\vec{\mathbf{p}}}{dt}| }[/math]). Two planets exerting attractive forces on each other will have the same change in momentum over the same amount of time. However if one planet is much larger it will have a much smaller change in velocity then the smaller planet. This is because p = mv and thus [math]\displaystyle{ {\Delta}v={\Delta}p/m }[/math]. So even though the forces will be the same, they may appear unequal due to a smaller change in velocity in a larger object.

The following image showcases the principle of reciprocity as the two people pulling exert an equal and opposite force on each other through tension. Also the object laying motionless on a surface has a net force of zero because the normal force of the table is equal to that of gravity on the object.

A Mathematical Model

The force due to gravity is:

[math]\displaystyle{ |\vec{\mathbf{F_g}}|=\frac{Gm_{1}m_{2}}{r^2} }[/math]

Although the force of gravity is dependent on the mass of both objects, both will experience the same magnitude of gravitational force. This can be clearly seen from the above equation.

The force due to electric interactions is:

[math]\displaystyle{ |\vec{\mathbf{F_{elec}}}|=\frac{1}{4{\pi}{\epsilon}_0}\frac{q_{1}q_{2}}{r^2} }[/math]

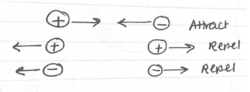
Electric charges that are of different sign will attract each other with the same magnitude of force. Furthermore, two like charges will repel each other, and the same magnitude of repelling force will act on each of the charges.

A more formulaic representation of the principle of reciprocity is as follows:

[math]\displaystyle{ \vec{\mathbf{F_{2 on 1}}}=\vec{\mathbf{F_{1 on 2}}} }[/math]

This can be represented in vector form as follows:

[math]\displaystyle{ \vec{\mathbf{F_{2on1}}} }[/math] = <F,0,0>
[math]\displaystyle{ \vec{\mathbf{F_{1on2}}} }[/math] = <-F,0,0>

from vpython import sphere, vector, arrow, color

Create two objects (spheres) with initial positions and masses

object1 = sphere(pos=vector(-5, 0, 0), radius=1, color=color.blue, mass=1) object2 = sphere(pos=vector(5, 0, 0), radius=1, color=color.red, mass=1)

Create arrows representing forces between the objects

force1_on_2 = arrow(pos=object1.pos, axis=vector(10, 0, 0), color=color.green) force2_on_1 = arrow(pos=object2.pos, axis=vector(-10, 0, 0), color=color.orange)

Set initial velocities for both objects

object1.velocity = vector(0, 0, 0) object2.velocity = vector(0, 0, 0)

Time step for the simulation

dt = 0.1

Main loop to update object positions and forces

while True:

   # Update positions of objects based on their velocities
   object1.pos += object1.velocity * dt
   object2.pos += object2.velocity * dt
   
   # Update force directions to always point from one object to the other
   force1_on_2.axis = (object2.pos - object1.pos).norm() * 10  # Force from object1 to object2
   force2_on_1.axis = (object1.pos - object2.pos).norm() * 10  # Force from object2 to object1
   
   # Update velocities based on forces applied (Newton's Second Law)
   object1.velocity += force1_on_2.axis / object1.mass * dt
   object2.velocity += force2_on_1.axis / object2.mass * dt

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

If you exert 20 N on the table, what would be the normal force of the table on you?

Since you are exerting 20 Newtons, due to reciprocity the table will be exerting a normal force of 20 Newtons.

If you push a box to the right with a force of 15 N, what is the magnitude and direction of the reciprocal force from the box on you?

The box exerts a force of 15 N on you towards the left.

Middling

A 60 kilogram man stands on the surface of the Earth. What is the force Earth exerts on the man? What is the force the man exerts on the Earth? Recall, due to reciprocity, the force that the Earth exerts on the man should be the same as the force that the man exerts on the Earth. We know how much the Man exerts on the Earth because he is standing on the Earth with a force equal to his weight.

[math]\displaystyle{ \mathbf{F_g}=mg=(60kg)(9.8\frac{m}{s^2})=588N }[/math]

Thus 588 N is the force that the man exerts on the Earth in the downwards direction. Because of reciprocity, the Earth must also be exerting 588 N on the man, but in the upwards direction.

A box is sitting on Earth's surface. The Earth exerts a force of 196 N on the box. What is the force on the Earth? What is the box's mass? Here, we have the force. Because of reciprocity, the force of the box on the Earth must also be equal to 196 N. Then, finding the mass of the box is relatively straightforward, as is seen below:

[math]\displaystyle{ m = F/g = 196N/9.8 = 20 kg }[/math]

Difficult

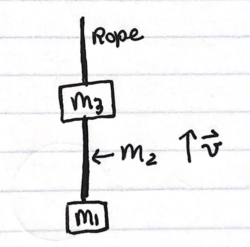
Two blocks of mass [math]\displaystyle{ m_1 }[/math] (under rod) and [math]\displaystyle{ m_3 }[/math] (above rod) are connected by a rod of mass [math]\displaystyle{ m_2 }[/math]. A constant unknown force F pulls upward on the top block while both blocks and the rod move upward at a constant velocity v near the surface of the Earth. The direction of the gravitational force on each block points down. Find [math]\displaystyle{ F_{1on2} }[/math], the magnitude of the force exerted by the bottom block on the rod.

See the diagram to the side for a depiction of the situation. Because the velocity is constant, the net force on the system, and thus on block 1, is equal to zero.

[math]\displaystyle{ F_{net}=0=F_{2on1}+F_g }[/math]

[math]\displaystyle{ \vec{\mathbf{F_{2on1}}}-m_{1}g\hat{\mathbf{y}}=0 }[/math]

[math]\displaystyle{ \vec{\mathbf{F_{2on1}}}=m_{1}g\hat{\mathbf{y}} }[/math]

Because [math]\displaystyle{ \vec{\mathbf{F_{1on2}}}=-\vec{\mathbf{F_{2on1}}} }[/math] it stands that:

[math]\displaystyle{ \vec{\mathbf{F_{1on2}}}=-m_{1}g\hat{\mathbf{y}} }[/math]

You are pulling a rope with a force of 15 N. The rope is connected to a box on a frictionless surface. The rope and box are moving at a constant rate. Find the force of the rope of the block, the block on the rope, and the rope on you.

Because the velocity of the system is constant, the net force on the system is equal to zero ([math]\displaystyle{ F_{net} = 0 }[/math]).

The Force of the rope on you is -15 N (equal and opposite to the force you are exerting on the rope)

The Force of the rope on the box is 15 N (this must be true in order to make the net force on the rope equal to zero)

The Force of the box on the rope is -15 N

Connectedness

The first physics I ever learned was Newtons laws. Before heading into any science class, I always thought, every reaction gets an equal and opposite reaction. I didnt really understand it. That is a fundamental principle that we use in almost all physics problems. It has been test questions and homework questions. The thing that intrigues me the most is how an ant can be pushing against a rhino and though the rhino is so much bigger, they are still exerting the same force.
I am an industrial engineering major and though there is very minimal use of physics in that field, I do believe it is something that will help us go about our days knowing that force isn't how much effort you put in but about the action reaction pairs.
Forces are something we deal with everyday. Everything we touch, me typing this page right now is all the result of forces. An important industry that deals with this is the automobile industry. If we understand the forces of the wheels on the road, we will know how to make wheels that best suit an automobile.
This topics is one of the fundamental underlying principles of physics. It applies to pretty much everything in physics.
Physics applies to almost any major. As an Environmental Engineer reciprocity is important to remember reciprocity, specifically in waste water management. Water pressure (force from water on pipe and force from pipe on water) is important when designing water infrastructure.
Reciprocity is important to remember in buildings. When creating a structure that can sustain a storm, you have to think about how high winds will change how parts of the structure interact with each other.
I remember back in elementary school the example that my teacher used was: when you kick a can, which experiences a greater force, the can or your foot? I was astonished to find out that both experienced a equal force due to reciprocity. I spent weeks kicking cans trying to understand this phenomenon until I learned for myself the forces were experienced relative to mass. This was my first real exposure to seeking to understand the world through the lens of physics.

8. This realization sparked my curiosity about the underlying principles of the natural world. I began to notice how reciprocity applies not just in the classroom but in everyday experiences, like the feeling of resistance when opening a heavy door or the bounce of a basketball.

9.Over time, I saw how this principle plays a role in more complex systems. For instance, in sports, the interaction between a bat and a ball demonstrates reciprocity—both objects exert forces of equal magnitude, resulting in the ball’s flight and the bat’s recoil.

10. This understanding became even more significant as I learned about its applications in engineering and design. Whether it’s creating durable bridges or ensuring safety in vehicles, the idea that forces are always equal and opposite helps guide innovations and problem-solving.

11. Reflecting on these lessons has deepened my appreciation for physics. Reciprocity is not just a theoretical concept but a fundamental truth that influences how we interact with the world around us.

History

Isaac Newton was born in Woolsthorpe, England. When he was a child, one day he was resting under an apple tree when suddenly an apple fell on his head. He thought about why things fall down and not fall back up. He spent years figuring out the phenomenon. After all this, he came up with three laws of motion. This is when he discovered gravitation as a force. Where Newton's Law comes into play is that the Earth is exerting a force on us to stay with it since closer objects exert stronger forces on each other. We are also exerting a force on Earth so that we stay on the ground and don't go flying off. The date of this story is not known, and some even believe it to be a myth. However William Stukeley, author of Memoirs of Sir Isaac Newton's Life noted that he had a conversation with Newton and Newton talked about why an apple falls to the ground due to gravitational interaction. Newton talked about why an apple falls to the ground due to gravitational interaction. This idea led to his formulation of the law of universal gravitation, which states that every mass attracts every other mass with a force proportional to the product of their masses and inversely proportional to the square of the distance between them. This was a groundbreaking realization, as it not only explained the falling apple but also described the motion of celestial bodies like the moon and planets.

Newton's insights into the nature of forces laid the foundation for classical mechanics and helped establish the concept of reciprocity in physics. His laws of motion, particularly the third law, provided the framework for understanding how forces between objects are always equal and opposite, whether those objects are on Earth or in space. These principles remain essential in both everyday experiences and advanced scientific research."

3: http://www.physicsclassroom.com/class/newtlaws/Lesson-4/Newton-s-Third-Law

4: http://www.schoolphysics.co.uk/age16-19/Mechanics/Statics/text/Vectors_in_equilibrium/index.html

5: Matter and Interactions By Ruth W. Chabay, Bruce A. Sherwood - Chapter 3.4

Reciprocity

Contents

The Main Idea

A Mathematical Model

Examples

Simple

Middling

Difficult

Connectedness

History

See also

Further reading

External links

References

Navigation menu