Quantum Properties of Light
Giovanny Espitia, Spring 2022
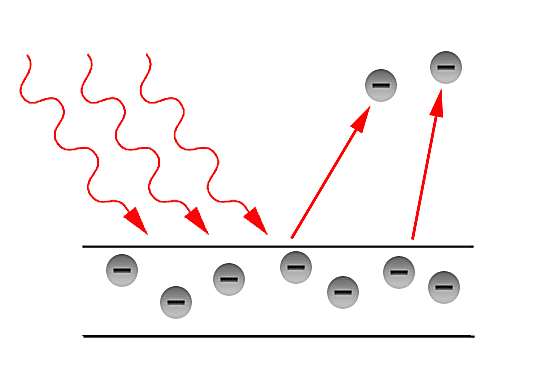
Why do we need a quantum interpretation? (History)
In the latter part of the 19th century, the classical description of light that had prevailed since the 17th century, began to fail in its explanatory power for the ever more precise measurements and phenomena being performed and observed in laboratories. The prime example of such failure is the so - called Ultraviolet Catastrophe. This term was first used by Paul Ehrenfest to refer to Rayleigh - Jeans law ability to predict experimental results below energies of [math]\displaystyle{ 10^{5} }[/math] and its sudden unexplained divergence at energies close to the ultraviolet range in the electromagnetic spectrum. Such discrepancies called for a more fundamental description of light. Fortunately, in the year 1900, Max Planck through his introduction of an ad - hoc assumption, was able to correctly explained the Black - body radiation problem. Planck later referred to such ad - hoc assumption as an "act of desperation". Moreover, in 1905, Einstein further validated the assumption made by Planck in his solution for the Black - body problem. The assumption was to treat light as if it came in discrete - packets later referred to as "Quanta". With such assumption, Einstein made further progress in explaining past experiments such as the Photoelectric effect first observed by Hertz in the latter part of the 19th century.
The Main Idea
Einstein, Planck, and Compton showed the explanatory power of giving light a discrete or quantum interpretation. In his theory of the photoelectric effect, Einstein showed that the energy [math]\displaystyle{ E }[/math] of a photon is simply the product [math]\displaystyle{ h\nu }[/math], where [math]\displaystyle{ h }[/math] is Planck’s constant and [math]\displaystyle{ \nu }[/math] is the frequency of the photon. As mentioned before, such treatment was allowed for the understanding of problems such as the Black - body, the Photoelectrons, and the scattering of electrons upon the contact of high energy electromagnetic radiation and light.
Mathematical Model
The energy of a photon
[math]\displaystyle{ E = h\nu }[/math]
Where:
- [math]\displaystyle{ h = 6.626*10^{-34} }[/math]
- [math]\displaystyle{ \nu = \frac{c}{\lambda} }[/math]
Here, [math]\displaystyle{ c }[/math] is the speed of light and [math]\displaystyle{ \lambda }[/math] is the wavelength of the photon.
Frequency - Wavelength Relationship:
[math]\displaystyle{ c = \lambda\nu }[/math]
Linear momentum of a photon
In the classical perspective, a photon should not carry any momentum since it is a massless boson. However, Einstein showed us through the following relationship that the former statement is not true.
[math]\displaystyle{ E = cp }[/math]
Where [math]\displaystyle{ c }[/math] is the speed of light and [math]\displaystyle{ p }[/math] is the momentum of the photon.
Therefore and according to the energy of a photon expression introduced in the previous subsection
[math]\displaystyle{ E = h\nu = cp }[/math]
Solving for [math]\displaystyle{ p }[/math],
[math]\displaystyle{ p = \frac{h\nu}{c} }[/math]
Interestingly, if we rearrange the above expression in terms of wavelength, we arrive at the same result as De Broglie for the wavelength of a matter wave. This is done as follows:
[math]\displaystyle{ p = \frac{h\nu}{c} }[/math]
Using the frequency - wavelength relationship introduced in a previous section, we make the appropriate substitution. Namely,
[math]\displaystyle{ p = \frac{h\nu}{c} = \frac{h}{\lambda} }[/math]
The last step, is simply to solve for [math]\displaystyle{ \lambda }[/math]. This step is left as an exercise to the reader.
Pair Production
When a photon has energy in the gamma - ray region of the electromagnetic spectrum and is close to an atomic nucleus, the product of such interaction often results in an electron - positron pair. A positron is the electron’s analog in antimatter. In other words, both have equal mass but a differing charge. This is often expressed as follows:
[math]\displaystyle{ \gamma \rightarrow e^{-} + e^{+} }[/math]
Where [math]\displaystyle{ \lambda }[/math] is the symbol for the photon and [math]\displaystyle{ e^{-}, e^{+} }[/math] are the symbols for the electron and positron, respectively. In order for pair - production to occur, the photon’s energy, [math]\displaystyle{ h\nu }[/math] must be larger than the rest mass energy, [math]\displaystyle{ 2m_{e}c^{2} }[/math], of the two particles.
Computational Model
For a model concerned with the quantum nature of light in terms of the double slit experiment, please access this website: https://ophysics.com/l4.html
Examples
Simple
An FM radio transmitter has a power output of 100 kW and operates at a frequency of 94 MHz. Compute the number of photons per second emitted by the transmitter.
Solution
We begin by computing the energy of the photon using the formula [math]\displaystyle{ E = h\nu }[/math]. In this case, the frequency is 94 MHz. Therefore,
[math]\displaystyle{ E = h\nu = (94\;MHz)\cdot 6.626e^{-34} = 6.23e^{-26}\;J }[/math]
The radio transmitter emits energy at a rate of 100 KJ/s. Thus,
[math]\displaystyle{ \frac{number\;of\;photons}{unit\;time} = \frac{energy/unit\;time}{energy/photon} = 1.61e^{30}\;s^{-1} }[/math]
Not trivial
A light source of wavelength [math]\displaystyle{ \lambda }[/math] illuminates a metal and ejects photoelectrons with a maximum kinetic energy of 1.00 eV. A second light source with half the wavelength of the first ejects photoelectrons with a maximum kinetic energy of 4.00 eV. Based on this information, determine the work function of the metal.
Solution
The following formula relates the maximum kinetic energy [math]\displaystyle{ K_{max} }[/math] of a photoelectron with the wavelength [math]\displaystyle{ \lambda }[/math] of the light producing the photoelectron and the work function [math]\displaystyle{ \phi }[/math] of the metal.
[math]\displaystyle{ K_{max} = \frac{hc}{\lambda} - \phi }[/math]
We then let [math]\displaystyle{ \lambda_{1} }[/math] and [math]\displaystyle{ \lambda_{2} }[/math] be the wavelengths of the light emitted by the first and second sources, respectively, and we let [math]\displaystyle{ K_{1} }[/math] and [math]\displaystyle{ K_{2} }[/math] be the maximum kinetic energies of the corresponding photoelectrons. Therefore,
[math]\displaystyle{ K_{1} = \frac{hc}{\lambda_{1}} - \phi }[/math]
[math]\displaystyle{ K_{2} = \frac{hc}{\lambda_{2}} - \phi }[/math]
where [math]\displaystyle{ \lambda_{2} = 0.5\;\lambda_{1} }[/math]
Therefore,
[math]\displaystyle{ K_{2}-2k_{1} = \phi }[/math]
Thus, [math]\displaystyle{ \phi = 2 }[/math] eV when [math]\displaystyle{ K_{1} = 1 }[/math] eV and [math]\displaystyle{ K_{2} = 4 }[/math] eV.
Challenging
A photon with momentum [math]\displaystyle{ p = \frac{h}{\lambda} }[/math] collides with a stationary electron. The photon scatters at an angle θ from the incident direction of the photon with momentum [math]\displaystyle{ p^{'} = \frac{hc}{\lambda^{'}} }[/math]. The electron scatters at an angle [math]\displaystyle{ \phi }[/math] from the incident direction of the photon with momentum [math]\displaystyle{ p_{e} }[/math] and energy [math]\displaystyle{ E_{e} = \sqrt{p_{e}^{2}c^{2} + m^{2}c^{4}} }[/math]. From this information, derive the compton formula ([math]\displaystyle{ \lambda^{'} - \lambda = \lambda_{e}(1-cos\theta) }[/math]).
Solution
We begin by noting that during the collision, the energy is conserved. Hence,
[math]\displaystyle{ pc + m_{e}c^{2} = p^{'}c + E_{e} }[/math]
and so is momentum in the direction of the incident photon:
[math]\displaystyle{ p = p^{'}cos\theta + p_{e}cos\phi }[/math]
and perpendicular to the direction of the incident photon:
[math]\displaystyle{ p^{'}sin\theta = p_{e}sin\phi }[/math]
Simpliflying the above equations,
[math]\displaystyle{ \frac{1}{\lambda} + \frac{1}{\lambda_{c}} = \frac{1}{\lambda^{'}} + \sqrt{\frac{1}{\lambda^{2}_{e}} + \frac{1}{\lambda^{2}_{c}}} }[/math]
[math]\displaystyle{ \frac{1}{\lambda} = \frac{cos\theta}{\lambda^{'}} + \frac{cos\phi}{\lambda_{e}} }[/math]
[math]\displaystyle{ \frac{sin\theta}{\lambda^{'}} = \frac{sin\phi}{\lambda_{e}} }[/math]
where we have written [math]\displaystyle{ p_{e} = \frac{h}{\lambda_{e}} }[/math]
Next, we eliminate [math]\displaystyle{ \phi }[/math] and [math]\displaystyle{ \lambda_{e} }[/math] from these equations. Eliminating [math]\displaystyle{ \phi }[/math] from the last two equations yields
[math]\displaystyle{ \frac{1}{\lambda_{e}^{2}} = \frac{1}{\lambda^{2}} + \frac{1}{\lambda^{'2}} - \frac{2cos\theta}{\lambda\lambda^{'}} }[/math]
Lastly, we must make the appropiate subsitution using the first simpliflied equation above. This proof is left as an exercise to the reader.
Connectedness
The understanding of various phenomena due to the quantum interpretation of light plays a significant role in our daily lives. From the development of the laser and thus its various derivatives, to the development of photovoltaic cells for the gathering of solar power, the leap forward taken by the pioneers of the quantum theory of light cannot be understated.
See also
The quantum interpretation of light gave a thorough explanation to various phenomena that had remained unexplained for the better part of the 19th century. For this reason, this page is intimately related to various others in this resource. To learn more about these subjects, click on them in the following list:
Further reading
HyperPhysics page on Photoelectric Effect: http://hyperphysics.phy-astr.gsu.edu/hbase/mod2.html#c
External links
References
http://hyperphysics.phy-astr.gsu.edu/hbase/mod2.html#c3 https://www.youtube.com/watch?v=dSUvyERhtO8
