Quantized energy levels

From Physics Book
Jump to navigation Jump to search

Que Le Fall 2023

The Main Idea

The negatively charged electrons around an atomic nucleus are held in orbit by attraction to the positively charged protons in the nucleus. Electrons are only permitted to exist in rigidly defined orbits known as a "stationary orbit" with specific radii which correspond to specific energy levels. The lowest energy and smallest radius orbit of one hydrogen electron has the exact same radius and energy level of any other hydrogen electron. This behavior occurs due to the wave-particle duality of electrons and results in a formulaic and regular behavior of energy levels in each stationary orbit. Because the energy levels of each orbit are not a continuous spectrum, and rather exist at discrete values, they are said to be 'quantized'. Quantization is a transition from a classical understanding of physical principles to a more modern understanding.

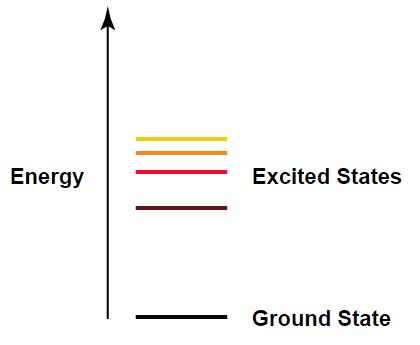
The various levels of energy and orbital radii associated with an electron are described using its principle quantum number (often denoted as [math]\displaystyle{ n }[/math]). A principle quantum number [math]\displaystyle{ n }[/math] of 1 indicates that the electron is in the orbit (or 'shell') closest to the nucleus; this state is of the lowest energy level and is referred to as the 'ground state'. A principle quantum number of greater than 1 indicates an electron in a larger orbit and higher energy level; this state is referred to as 'excited'. Less energy is required to free an electron from an excited state.

The energy levels and radii of orbiting electrons are rigid and not continuous. When an electron transitions to an orbit of greater radius and thus higher energy it does so automatically. At the ground state (n = 1) an electron orbiting Hydrogen has an energy of -13.1 eV and orbits the atom at a radius of 0.0529 nm. At the first excited state (n = 2) the electron has an energy of -3.275 eV and orbits at a radius of .2116 nm. The electron at no point has an energy between -13.1 eV and -3.275 eV and at no point exists between .0529 nm and .2116 nm, but rather only at those exact values and any change between them is instantaneous. This phenomenon is similar to jumping up and down a flight of stairs. You can only stand on the steps and no where in between. Similarly, the electron can only exist at the exact radii and energy levels given by plugging its principle quantum number [math]\displaystyle{ n }[/math] into the relevant formulas. In problem sets this number will either be given or easily derived from given information.

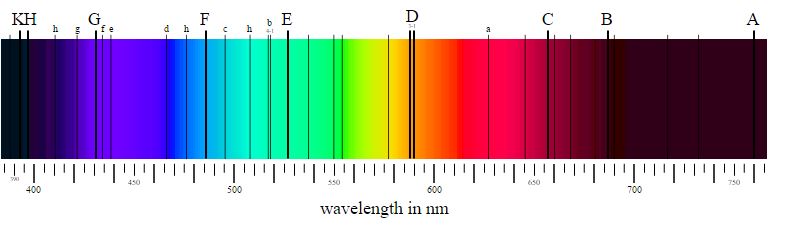
If light is shone through a gas, the gas will absorb the specific wavelengths characteristic of the atoms in the gas. If the light were to be put through a prism of light or a diffraction grating, then there would be absorption lines, or places where the wavelength of light had been absorbed into the gas. This process creates something called an absorption spectrum. Similarly, if this same gas was heated to the right temperature, it would emit the same wavelengths that it absorbed before. Putting this emitted light through a prism or diffraction grating would create an emission spectrum. This is the opposite of an absorption spectrum because it shows the emission lines from the gas instead of the absorption lines.


Mathematical Model


1) The energy of each level can be found using the formula: [math]\displaystyle{ E_n = {\frac{-13.6 eV}{n^2}} }[/math]

  • Where [math]\displaystyle{ n }[/math] is the principle quantum number. The value will always be negative because electrons in the electron cloud are in a bounded state, so the potential energy is negative.

Formula Derivation: [math]\displaystyle{ E_{total} = K+U_{electromagnetic}=\frac{mv^2}{2}+(-\frac{\frac{1}{2}\frac{1}{4\pi\epsilon_0}\frac{me^2}{\hbar}}{N^2})=-\frac{1}{2}\frac{me^4}{(4\pi\epsilon_0)^2\hbar^2}\frac{1}{N^2} }[/math]


2) Radius of orbit: [math]\displaystyle{ r_{n} = a_{0}n^2 }[/math]

  • Where [math]\displaystyle{ a_{0} = {\frac{4π ε_{0}ħ^2}{m_{e}e^2}} = 0.0529 }[/math] nm


Where this formula is from:

For any hydrogen atom, an electron (mass m, charge -e) orbits a proton (mass M, charge +e) in a circular orbit of radius r. The equation for the orbital speed of the electron (by assuming it's constant) can be set up using the fact that the electrostatic force between two charges is equivalent to the centripetal force that keeps the electron orbiting the nucleus: [math]\displaystyle{ \frac{mv^2}{r}(-\hat r)=\frac{kq_1q_2}{|r^2|}(\hat r) }[/math], where [math]\displaystyle{ k = \frac{1}{4\pi\epsilon_0} }[/math], [math]\displaystyle{ q_1 }[/math] and [math]\displaystyle{ q_2 }[/math] are respectively the charge for an electron and a proton (-e and +e).

Hence we know that [math]\displaystyle{ v = \sqrt{\frac{1}{4\pi\epsilon_0}\frac{e^2}{mr}} }[/math] [1]

As we know from the background information, Niels Bohr corrected Rutherford's planetary model by proposing every electron's translational angular momentum is quantized: [math]\displaystyle{ |\vec L_{trans,\ nucleus}|=N\hbar }[/math]

Where "N" is the orbit numbers[math]\displaystyle{ (= 1,2,3...) }[/math] and [math]\displaystyle{ \hbar=\frac{h}{2\pi}=1.05\times10^{-34} }[/math] with "h" plank's constant.

Moreover, by the definition of angular momentum, its magnitude is given by [math]\displaystyle{ |\vec L|=|\vec r\times\vec p|=rmv }[/math], where "r" is the perpendicular distance from the center of the nucleus to the orbit (i.e. the orbital radius) and "mv" is the linear momentum of an individual electron.

Using the two equations derived, we can obtain a way of calculating the velocity: [math]\displaystyle{ v=\frac{N\hbar}{mr} }[/math] [2]

Combining equations I and II, we can determine how to calculate the orbital radius (r) simply using some constants, the mass m, and the orbital number N: [math]\displaystyle{ r=\frac{4\pi\epsilon_0N^2\hbar^2}{me^2} }[/math]


3) The energy of a photon is associated with wavelength by [math]\displaystyle{ E = \frac{hc}{\lambda} }[/math]


While the value for each energy level is set in place, the energy of each individual electron can change. This can happen either by an interaction with another electron or a photon. Any electron can jump from the ground state to the fourth level if it receives enough energy to match the energy of the fourth level.

Computational Model


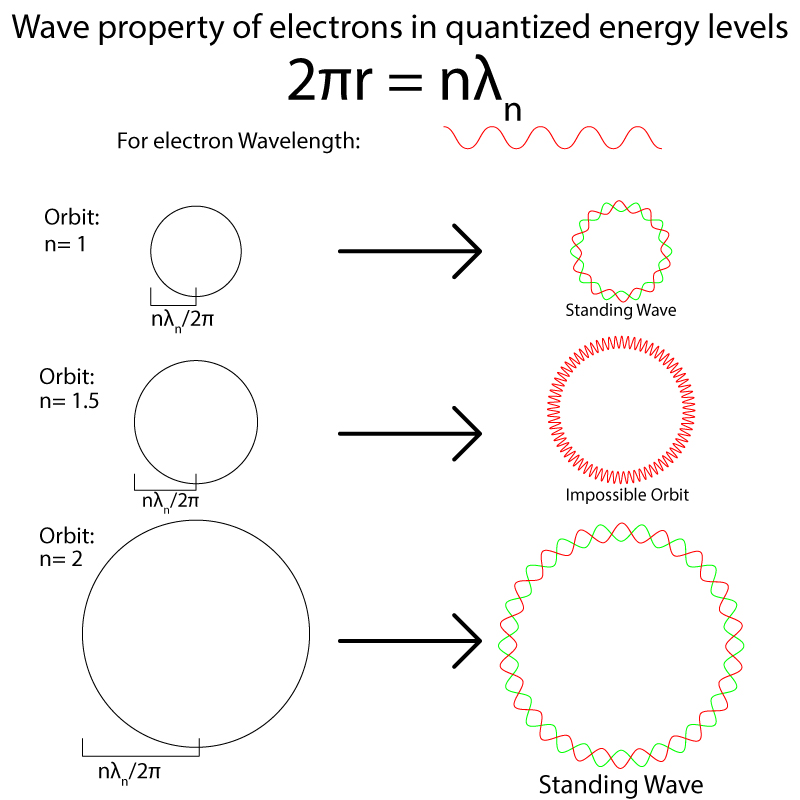
The radii of orbits are restricted to certain values due to the wave nature of electrons. Electrons can only exist happily in standing waves and the waves created by an orbit will only be standing if the wavelength follows the formula [math]\displaystyle{ 2pi*r = n }[/math]λ[math]\displaystyle{ _n }[/math]


Consider a wave of λ = 1 and a series of orbits with varying radii. If that wave is laid along the circular path of the orbit, there are only a few specific circumferences that will allow the wave to fit perfectly, forming a standing wave. Any length where the wavelength does not form a standing wave will cause patterns of interference and a stable orbit would be impossible.

Examples

Simple

What is the principle quantum number of an electron orbiting a hydrogen atom with an energy of -.544eV?

1) [math]\displaystyle{ E_{n} = \frac{-13.6 eV}{n^2} }[/math]

2) [math]\displaystyle{ \frac{-13.6eV}{n^2} = -.544eV }[/math]

3) [math]\displaystyle{ n^2 = \frac{-13.6eV}{-.544eV} }[/math]

4) [math]\displaystyle{ n = 5 }[/math]

The Bohr model of the hydrogen atom pictures the electron in its ground state orbiting the proton at a distance of [math]\displaystyle{ 5.3*10^{−11} m }[/math] at a speed of [math]\displaystyle{ 2.5*10^6m/s }[/math]. What is the escape velocity in this model?

1) [math]\displaystyle{ F_e = ma }[/math]

2) [math]\displaystyle{ \frac{kqq}{r^2} = m(\frac{v_t^2}{r}) }[/math]

3) [math]\displaystyle{ \frac{kqq}{r} = m*v_t^2 }[/math]

4) [math]\displaystyle{ v_t = \sqrt(\frac{kq_1q_2}{m_er_{orbit}}) }[/math]

5) [math]\displaystyle{ \sqrt(\frac{8.9*10^9*2*(1.6*10^{-19})^2}{5.3*10^{−11}*9.1*10^{-31}}) }[/math] 

   k = 8.9*10**9 # coulombs 
   q = 1.6*10**-19 #charge of electron
   m_e = 9.1*10**-31 # mass of electron
   r = 5.3*10**-11 #radius of orbit
   print(((2*k*q*q)/(m_e*r))**0.5)

Medium

What is the difference in energy between an electron orbiting a hydrogen atom in the [math]\displaystyle{ n }[/math] = 1 orbit, or ground state, and an electron orbiting a different hydrogen atom in the third excited orbit?


1) ∆[math]\displaystyle{ E_{n} }[/math] = [math]\displaystyle{ E(4) - E(1) }[/math]

  • The third excited state is the n = 4 state

2) ∆[math]\displaystyle{ E_{n} }[/math] = [math]\displaystyle{ {\frac{-13.6eV}{4^2}} - {\frac{-13.6eV}{1^2}} }[/math]

3) ∆[math]\displaystyle{ E_{n} }[/math] = [math]\displaystyle{ -13.6eV({\frac{1}{16}} - {\frac{1}{1}}) }[/math]

4) ∆[math]\displaystyle{ E_{n} }[/math] = [math]\displaystyle{ -13.6eV({\frac{-15}{16}}) }[/math]

5) ∆[math]\displaystyle{ E_{n} }[/math] = [math]\displaystyle{ 12.75eV }[/math]

Challenging

What is the energy of a Hydrogen electron in an orbit of radius .4761 nm?

Using the formula for the radius of the orbit, find the value of n for this electron:

1) [math]\displaystyle{ r = a_{0}n^2 }[/math] where n =1,2,3... and the Bohr Radius [math]\displaystyle{ a_{0} = 0.0529*10^{-9} }[/math]

2) [math]\displaystyle{ n^2 = \frac{r}{a_{0}} = \frac{.4761*10^{-9}}{0.0529*10^{-9}} = 9 }[/math]

Using the value of n, calculate the energy of the electron:

3) [math]\displaystyle{ E_{n} = \frac{-13.6 eV}{n^2} = \frac{-13.6 eV}{9} = -1.51 eV }[/math]

Implications

Until quantization of atomic energy levels occurred, there were a few different experiments that had already been performed that did not make sense. Once researchers discovered the actual way electrons make up the electron cloud as well as the mechanisms that help them jump from level to level, these experiments could be explained. Readings for these three experiments can be found below.

  1. Blackbody Radiation
  2. Photoelectric Effect
  3. Emission Spectra of Atoms

The quantization of energy levels is a fundamental principle of quantum mechanics that applies to all quantum systems, including atoms. It arises from the wave-particle duality of matter, which means that particles like electrons can exhibit both wave-like and particle-like behavior. The quantized energy levels of electrons in atoms have important implications for chemical reactions and the properties of materials, such as the absorption and emission spectra of atoms and molecules. Spectroscopy is a powerful tool that utilizes these principles to study the structure and behavior of matter at the atomic and molecular scale. Additionally, the quantized energy levels of electrons are responsible for chemical bonding, which underlies all of chemistry. When atoms come together to form a molecule, their outermost energy levels interact to form new hybrid energy levels that determine the molecule's properties. Therefore, the quantization of energy levels is a crucial concept in understanding the behavior of matter and light in the quantum world.


History

In 1814, Joseph von Fraunhofer and William Hyde Wollaston discovered that when viewed closely, the spectrum from sunlight contained dark lines. These lines represented wavelengths of sunlight that were not reaching us. These wavelengths were being absorbed by the sun's atmosphere.

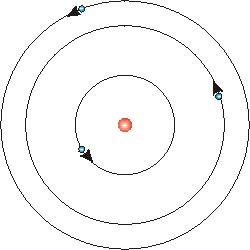
This is a model of the Bohr atom. It shows different levels for the electrons to orbit the nucleus.

In 1911, Rutherford came up with his model for the atom. It used many of the same components of an atom that we know exists today, but it had one glaring issue. His model lacked stability. Classical electromagnetic theory said that the electrons surrounding the nucleus would quickly collapse because they were emitting electromagnetic waves during acceleration, causing them to lose energy. If this were true, then the atom as we know it would not be able to exist at all.


Bohr's model of the atom solved this problem. He proposed that the laws of classical mechanics must be reconsidered. His model said that the electron cloud had stationary orbits, a specific set of orbits for electrons. This differed from the assumption that the electron cloud was just a continuum where the electrons were free to orbit the nucleus. His model was similar to the solar system in that electrons orbit the nucleus like planets orbit the sun. Electrons are held in place by electrostatic forces, and planets are held in place by gravitational forces.

References

Retrieved from "http://www.physicsbook.gatech.edu/index.php?title=Quantized_energy_levels&oldid=46723"