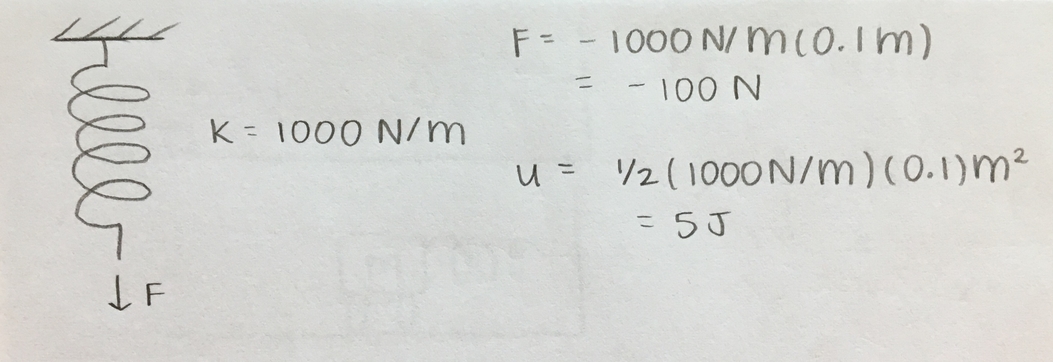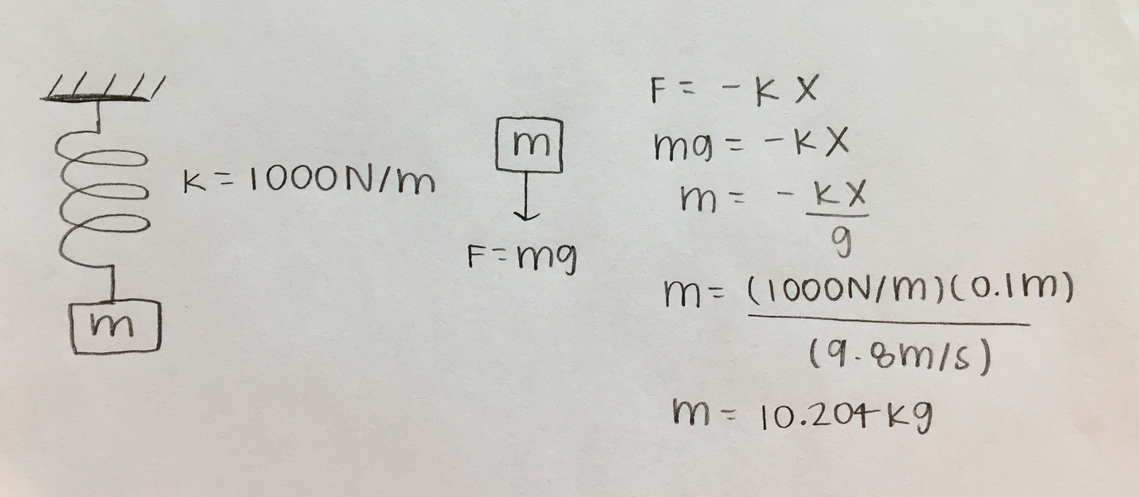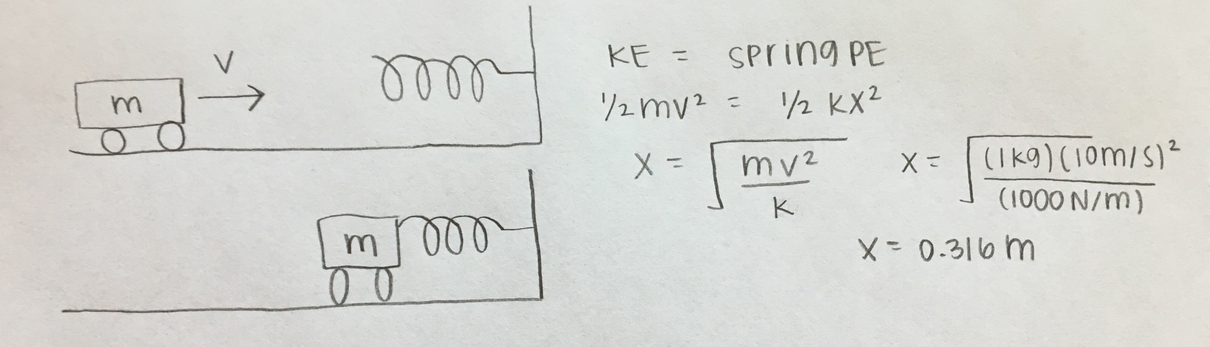Potential Energy of Macroscopic Springs
An Exploration of Spring Potential Energy: Lanier Freeman and other
Claimed by Hailey Lindstrom for Spring 2017
The Main Idea
A macroscopic ideal spring is an elastic device which stores potential energy when stretched or compressed. Ideal springs exert a force which is linearly proportional to its change in length. This relationship can be modeled by the equation F = -kx, where F is the force, k is the spring constant in N/m or lb/in, and x is the change in length of the spring from its equilibrium length.
A Mathematical Model
The equation for potential energy of a spring can be mathematically shown by integrating Hooke's Law.
- We start with the initial equation for Force of a macroscopic spring, which is equal to:
[math]\displaystyle{ F = kx }[/math]
- We then integrate with respect to x so that we can obtain work (which is equal to the integral of force):
[math]\displaystyle{ \int F\ dx = \int kx\ dx }[/math]
- Finally, we solve the indefinite integral which gives us the final equation for work of a macroscopic spring.
[math]\displaystyle{ W = \frac{1}{2}kx^2 }[/math]
Here, work is equal to the elastic spring potential energy, [math]\displaystyle{ \Delta U_{spring} }[/math].
A Computational Model
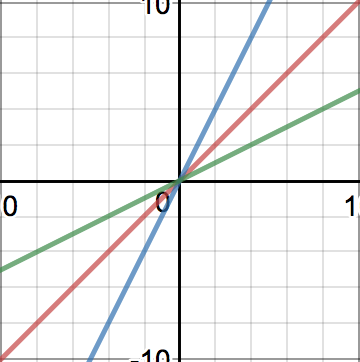
Below is a graph of force versus displacement for a macroscopic spring with different spring constants (k values). The x axis is displacement in meters and the y axis is in Newtons. This shows that there is a linear relationship between change in length and force.
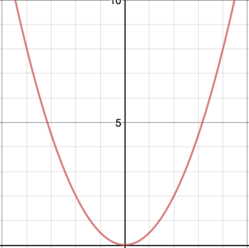
Represented here is the potential energy of the macroscopic spring as a function of the change in length of the spring. The x axis is displacement in meters and the y axis is energy in Joules. This shows that the relationship between change in length and potential energy is quadratic.
Examples
Simple
Question
If a spring has a spring constant, k = 1000 N/m, and is stretched 10 cm, find the force and potential energy of the spring.
Solution
Moderate
Question
If a spring has a spring constant, k = 1000 N/m and is stretched 10 cm by an unknown mass, find the unknown mass.
Solution
Difficult
Question
If there is a cart of mass, m = 1 kg, moving at speed, v = 10 m/s^2, and it collides with a spring of spring constant, k = 1000 N/m, how far does the spring compress? You can ignore friction in this example!
Solution
Connectedness
Hailey's Answers
1. How is this topic connected to something that you are interested in? The topic of macroscopic springs is actually much more interesting to me than I originally thought before creating this wiki page. There are so many practical applications of springs in the real world that make life much easier. For example, springs are used in cars, particularly in shock absorbers, and this helps us to drive more safely. Another use of springs that we all use is everyday is the springs within the mattress of our bed. Having the right spring stiffness (k value) is really important because it provides you with a great (or little) amount of support and comfort while sleeping.
2. How is it connected to your major? This concept is related to my major in the sense that solving potential energy or force for a macroscopic spring requires a basic understanding of calculus - particularly integrals. In addition, some of the more difficult spring problems require a higher understanding of mathematic equations as they relate to something else (in this case, it is physics). This skill is something that is useful in industrial engineering because it deals with a lot of applying mathematic equations to different concepts.
3. Is there an interesting industrial application? As stated above, springs are used a lot in the automobile industry. One thing that I found really interesting was that the use of springs in vehicles actually allows for massive amounts of weight to be supported. They are able to work with the shock absorbers to help absorb larger weights than the vehicle on its own would be able to support. They also help in flexibility of automobiles which helps to provide for a smoother ride.
Lanier's Answers
1. This topic is of much interest to me because of the applications of the mean value theorem of calculus to problems dealing with potential energy--both spring and gravitational. I think this type of problem underscores the amazing power of the MVT.
2. This topic relates to being a math major for obvious reasons; it presents a basic, practical application for advanced mathematics, something that isn't seen often in my experience.
3. A silly yet decent example of industrial applications of spring applications is the way many pens are constructed: a spring of specific dimensions requiring a spring constant within a certain range is necessary to make the button on a pen work.
History
Before the existence of coiled springs, leaf springs were used. These springs consisted of curved strips of metal clamped to one another. However, these were not very efficient because they always had to be lubricated and squeaked a lot. It was not until 1763 when R. Tradwell invented the first coiled spring. Finally in 1857 when a steel coil spring was invented. Springs progressed and within just a century, springs have been used in many different things and have substantially improved the car and machine industry.
- William Rankinet
- The term potential energy was introduced as e, although it has links to Greek philosopher Aristotle's concept of potentiality.
- Scottish engineer and physicist
- Robert Hooke
- Came up with Hooke's Law, which is used to find the potential energy of springs.
- Coined the term "cell" in biology
See also
Further reading
External Links
Good explanation (and calculator) for potential energy in macroscopic springs: [1]