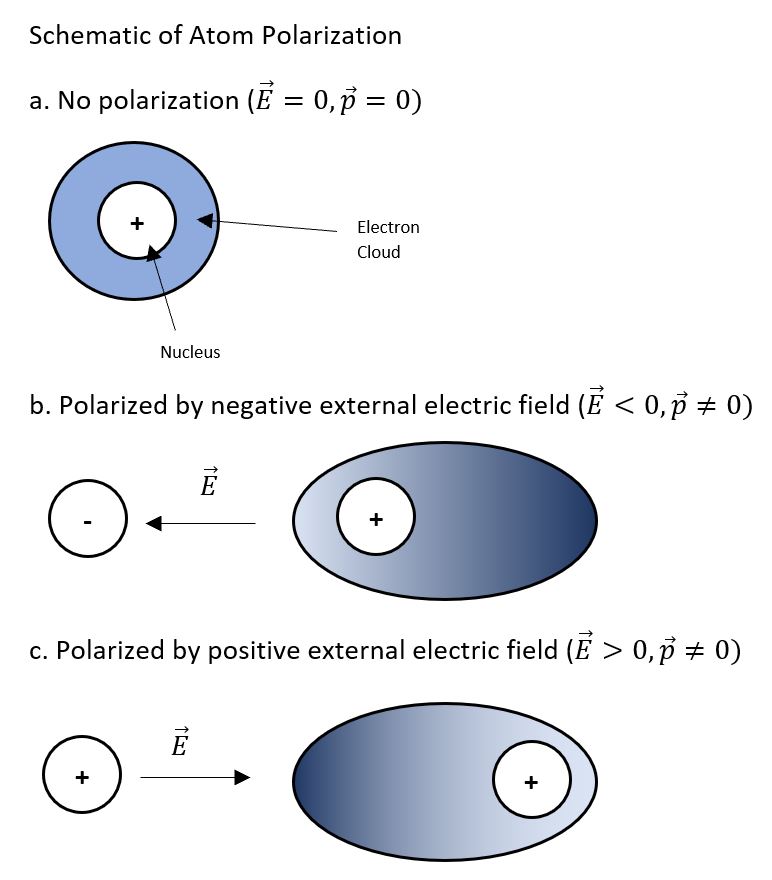
Polarization of an Atom

Edited by Amie Yang - Spring 2023

This page serves to outline and explain the inner workings and hidden mechanisms of the polarization of an atom.

Introduction

Atoms are basic units of matter, consisting of different charged particles. An atom contains a nucleus made of protons (with +e charge) and neutrons (neutral) which is surrounded by an "electron cloud" defined by a space where electrons (with -e charge) exist. While electrons are attracted to the nucleus and therefore generally remain near the the nucleus, electrons can also be shifted by external charges. These external charges therefore allow electrons to shift so that the electron cloud is no longer centered on the nucleus, and this results in an symmetric distribution of charge allowing the atom to be "polarized".

More specifically, these external charges create apply an electric force on atom constituents. For example, if a positive charge is placed to the left of an atom, an electric field will be created that shifts the electron cloud of the atom towards the positive charge (to the left) and will shift the net positive nucleus away from the charge (to the right) as two objects of the same charge repel each other. In this case, it is now more probable to find an electron to the left of the nucleus, rather than the right.

The polarization of atoms plays a crucial role in various scientific phenomena and technological applications. When atoms become polarized, they can interact with other polarized atoms or molecules, leading to a range of forces and effects. For instance, the temporary polarization of nonpolar molecules gives rise to London dispersion forces, which are weak attractive forces that significantly influence the physical properties of substances. Furthermore, the polarizability of atoms and molecules can impact their behavior in electric fields, which is essential for understanding their roles in electronic devices, chemical reactions, and spectroscopy. By studying atomic polarization, researchers can gain a deeper understanding of atomic and molecular interactions, paving the way for advancements in materials science, electronics, and chemistry.

Calculations Relating to Polarization of Atoms

The following are equations mediating these interactions. First and most importantly, electric fields are the product of field source charge and the distance to the observation location at which you would like to find the electric field value. Coulomb's Law allows us to calculate this for a point charge:

[math]\displaystyle{ {\vec{E} = \frac{1}{4\pi\varepsilon_0} \frac{q}{r^2}} }[/math] [math]\displaystyle{ {\hat r} }[/math]

where E is the electric field at the observation point, q is the charge of the particle creating the electric field, and q is a vector from the source of the field to the observation location.

This electric field then can apply a force onto charge particles at the observation locations, a force that is quantified by the following equation.

[math]\displaystyle{ {\vec{F} = q\vec{E}} }[/math]

where F is the force created by the electric field E and the charge of a particle q. Note that q in this equation is the charge of the particle being affected by the electric field, NOT the charge of the particle causing the electric field. For example, this would be the charge of an electron if we were calculating the force on the electron by an external electric field.

This force is what causes the atom to become polarized. This force is responsible for "polarizing" an atom by accelerating the electrons and shifting the electron cloud of an atom.

Once an atom is polarized, it forms an induced dipole. A "dipole" is a pair of equal and oppositely charged particles. In this case, these particles are comprised of the nucleus (which is positively charged) and the electron cloud (which is negatively charged). This dipole is "induced" as it was formed as a result of an external, temporary force and would return in a non-dipole state if this external force was removed. In physics, this dipole is quantifiably characterized by it's dipole moment, which can be calculated through the following equation:

[math]\displaystyle{ {\vec{p} = qs} }[/math]

where p is the dipole moment of the polarized atom, q is the magnitude of their charge, s is the distance between the constituents of the dipole. Note that q is NOT the cumulative charge of each dipole constituent, but rather their individual, shared charge. For example, if I had a dipole made of one electron and one proton (which would be accompanied by a neutron, but this does not affect the charge) q would equal e (the charge of a proton), not 2e.

The previous equation characterizes the dipole moment solely from values describing the dipole. A dipole moment can also be predicted if the electric field inducing the dipole moment, and the "polarizability" of the material being polarized is known via the following equation:

[math]\displaystyle{ {\vec{p} = α\vec{E}} }[/math]

This shows that the dipole moment is directly proportional to the magnitude of the applied electric field E. The constant α is called the "polarizability" of a particular material. Many of these polarizability values have been measured experimentally and can be found in reference volumes.

Example Problems

Now that you understand the basics of atom polarization and induced dipoles, try some example problems! Be sure to show all steps in your solution and include diagrams whenever possible. Problems are ranked relatively from easy to moderate.

Easy

Suppose that you have a negatively charged tape hanging from the desk, and you rub a wooden pencil on a wool sweater and bring it near the tape.

If the tape swings toward the pencil, does this show that the pencil had been positively by rubbing it on the wool?

Not necessarily. Even if the pencil is uncharged, the charged tape will polarize the and be attracted by the induced dipoles.

Can a charged object repel a neutral object? Why or why not?

Polarization always brings the unlike-sign charge closer, yielding a net attraction. Repulsion of an induced dipole can't happen. Therefore repulsion is the better test of whether an object is charged.

Calculate the induced dipole moment of an atom in an external electric field.

Given:

An external electric field E = 1.0 x 10^5 V/m

The polarizability of the atom α = 1.0 x 10^-40 C^2/m^2

Solution: p = α * E p = (1.0 x 10^-40 C^2/m^2) * (1.0 x 10^5 V/m) p = 1.0 x 10^-35 C*m

Moderate

Why are charged objects attracted to neutral objects?

The attraction of both positively and negatively charged invisible tape to your hand, and to many other neutral objects, is deeply mysterious. The net charge of a neutral object is zero, so your neutral hand should not make an electric field that could act on a charged tape, nor should your neutral hand experience a force due to the electric field made by a charged tape. Nothing in our statement of the properties of electric interactions allows us to explain this attraction!

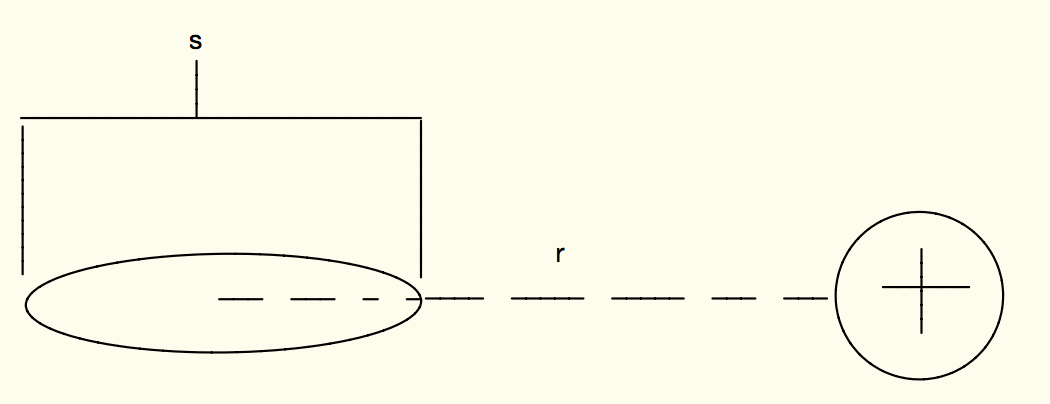
A positive point charge with charge q acts on a an atom as shown below.

What is the electric dipole moment p of the atom?

[math]\displaystyle{ {\vec{p} = α\vec{E}} }[/math]

[math]\displaystyle{ E=\frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} \hat{r} }[/math]

[math]\displaystyle{ p=\frac{\alpha}{4 \pi \epsilon_0 } \frac{q}{r^2} \hat{r} }[/math]

What is the magnitude and direction of the electric force due to the induced electric field on the point charge? Assume the magnitude of the charge for either end of the dipole is q, and that r is much larger than s.

[math]\displaystyle{ Emag=\frac{1}{4 \pi \epsilon_0 } \frac{2q^2s}{r^3} \hat{r} }[/math]

The [math]\displaystyle{ q^2 }[/math] in this equation comes from the fact that we multiply the Electric field by the charge it is acting on to get the electric force. The direction of this force will be in the negative x direction, since the negative end of the atom would be polarized closer to the positive point charge, and thus the force acting due to the electric field would also be in that direction.

Calculate the potential energy of an induced dipole in an external electric field.

Given:

An external electric field E = 5.0 x 10^4 V/m

The polarizability of the atom α = 2.0 x 10^-40 C^2/m^2

The angle θ between the direction of the induced dipole and the electric field is 60 degrees.

p = α * E p = (2.0 x 10^-40 C^2/m^2) * (5.0 x 10^4 V/m) p = 1.0 x 10^-35 C*m

U = -p * E * cos(θ)

θ = 60 degrees * (π/180) = π/3 radians

U = -(1.0 x 10^-35 Cm) * (5.0 x 10^4 V/m) * cos(π/3)

U = -(1.0 x 10^-35 Cm) * (5.0 x 10^4 V/m) * (1/2)

U = -2.5 x 10^-35 J

Advanced

How does the difference in atomic polarizability between two materials affect their dielectric constants and their behavior as insulators or conductors when subjected to an external electric field?

The atomic polarizability of a material influences how well it can store electrical energy and resist conducting electricity when exposed to an electric field.

If a material has a high atomic polarizability, its atoms are more easily affected by an electric field. This means the material can store more electrical energy without allowing electricity to flow through it. This makes it a better insulator.

On the other hand, if a material has a low atomic polarizability, its atoms are less affected by an electric field. As a result, it can't store as much electrical energy and may not be a good insulator.

Calculate the change in the polarizability of an atom when subjected to an external electric field.

Given:

The initial polarizability α_0 = 4.0 x 10^-40 C^2/m^2

The applied electric field E = 1.2 x 10^4 V/m

The polarizability constant K = 3.0 x 10^-10 C^2/m^4

Calculate the change in polarizability (Δα) of the atom when subjected to the external electric field.

Δα = K * E^2

Δα = (3.0 x 10^-10 C^2/m^4) * (1.2 x 10^4 V/m)^2

Δα = (3.0 x 10^-10 C^2/m^4) * (1.44 x 10^8 V^2/m^2)

Δα = 4.32 x 10^-40 C^2/m^2

Applicability in Everyday Life

How is this topic connected to something that you are interested in?

Atoms are the composition of all life. Anything can be broken down into atoms and subatomic particles. If we are able to understand atoms we understand the fundamental concepts of all life, and that is pretty interesting in my opinion.

How is it connected to your major?

Polarization of atoms is relevant to my major of Biomedical Engineering as all life is possible because of atomic interactions resulting from atom polarization! However, even if your major is not within biology or chemistry, many of us are required to take classes such as Intro to Physics 2 and Chemistry where the polarization of atoms directly applies.

Is there an interesting industrial application?

There are many interesting industrial applications of the polarization of atoms over a broad scope of fields.
The polarization of atoms is what causes something known as van Der Waals forces, which are attractive forces between molecules or atoms that are weaker than traditional covalent or ionic bonds, but still play a fundamental role in the behavior of such particles. These forces are what allow creatures like spiders and geckos to scale walls, as the van Der Waals forces between small hairs for spiders and another adhesive material for geckos interact with the particles of the surface being scaled, and are strong enough to support the animal. Using technology that mimics this behavior, mechanical and materials engineering labs have created basic prototypes for tools that can allow humans to scale walls in the same fashion, which could be applied for construction work, rescue utility, and countless other applications.

Some of these include:

Chemistry

Checking chirality of organic compounds
Infrared spectroscopy

Astronomy

Providing information on sources of radiation and scattering, polarization probes the interstellar magnetic field
Polarization of cosmic microwave background is being used to study the physics of the early universe

3D Movies

Images are projected from the projector with multiplexed polarization
3D glasses with suitable polarized filters ensure that each eye receives only the intended image

Communication and Radar

All radio transmitting and receiving antennas are intrinsically polarized-think FM and AM radio
Vertical polarization is used to radiate a radio signal in all directions, such as those used in mobile phones
Alternating vertical and horizontal polarization allows satellite communication systems to broadcast two separate transmissions on a single frequency

Material Science Engineering

the relationship between strain and birefringence motivates the use of polarization in characterizing the distribution of stress and strain in prototypes

Navigation

Sky polarization was used in the 1950s when navigating near the poles of the Earth's magnetic field when neither the sun nor stars were visible

History

The history of the polarization of atoms can be traced back to several key developments in the field of physics and chemistry. Here is a brief overview of some of the milestones:

Coulomb's law (1785): Charles-Augustin de Coulomb found a law that describes how charged particles interact. This helped us understand how charges in atoms can cause polarization.

Discovery of the electron (1897): J.J. Thomson found the electron, a tiny charged particle in atoms. This was important for understanding how atoms can be polarized by electric fields.

Rutherford's atomic model (1911): Ernest Rutherford created a model of the atom with a central nucleus and orbiting electrons. This model helped us understand how atoms can be polarized.

Bohr's atomic model (1913): Niels Bohr improved Rutherford's model by adding the idea of specific energy levels for electrons. This helped us understand how electrons react to electric fields and how atoms can be polarized.

London dispersion forces (1930): Fritz London explained weak attractive forces between nonpolar atoms or molecules due to temporary polarization. This helped us understand how polarization affects interactions between atoms and molecules.

Quantum mechanics (1920s-1930s): Scientists like Werner Heisenberg, Erwin Schrödinger, and Paul Dirac developed quantum mechanics, which better describes atoms and their behavior. This helped us understand atomic polarization even more.