Particle in a 1-Dimensional box
claimed by Eathan 4/14/2022
The time-independent Schrodinger Equation is a partial differential equation whose solutions describe the wave function of a quantum system. It is given in the following form. [math]\displaystyle{ -\frac{\hbar^2}{2m}\frac{\partial^2\psi(x)}{\partial x^2} + V(x)\psi(x)= E \psi(x) }[/math]
where
[math]\displaystyle{ \hbar }[/math] is the reduced Planck constant
[math]\displaystyle{ m }[/math] is the mass of the particle
[math]\displaystyle{ \psi(x) }[/math] is the wave function
[math]\displaystyle{ V(x) }[/math] is the potential of the system
[math]\displaystyle{ E }[/math] is the energy of the system
Main Idea
We can solve the Schrodinger Equation by considering its boundary conditions and applying continuity to them. We will showcase 2 cases of the particle in a 1-Dimensional box: an infinite well and a semi-infinite one.
Infinite Potential (Mathematical Model)
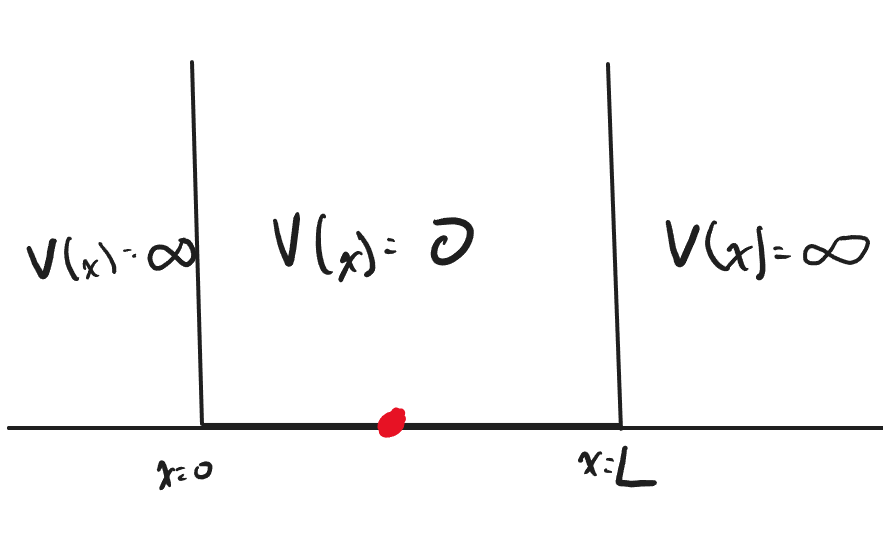
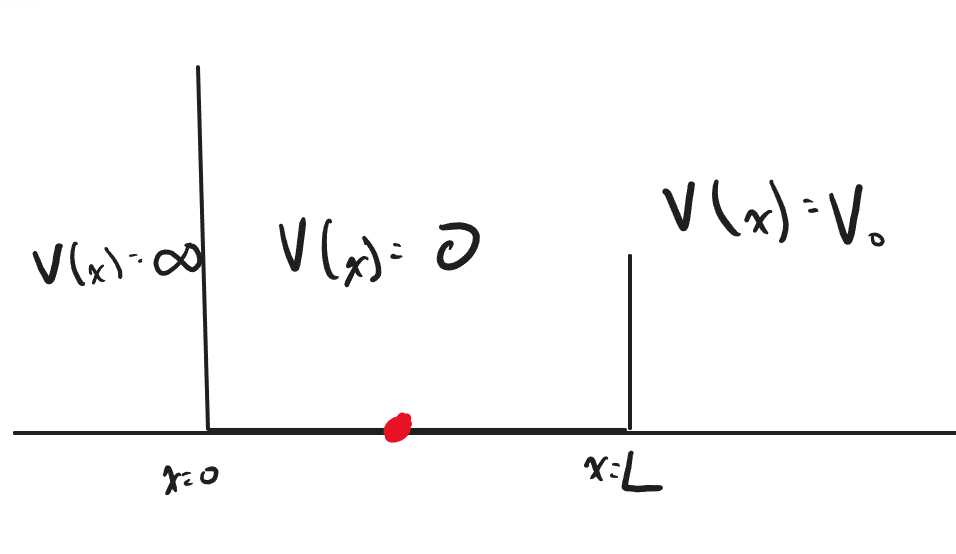
We will first consider the following scenario: The particle in a 1-Dimensional box is a quantum system in which a particle is bounded in a well with infinite energy at the barrier. Since the barriers of the well are infinite, there should be a 0% chance of finding the particle outside the well. We will apply this boundary condition later as we derive the solution to the particle in a 1-Dimensional box
Imagine the quantum system shown above, where the particle is bounded by infinite potential energy at [math]\displaystyle{ x = 0 }[/math] and [math]\displaystyle{ x = L }[/math]. The system also has 0 potential energy within the boundaries. We will use these as our boundary conditions to solve for the wave function [math]\displaystyle{ \psi(x) }[/math] below.
We will begin to solve the Schrodinger equation with the boundary conditions as shown above. From the points [math]\displaystyle{ x = 0 }[/math] to [math]\displaystyle{ x = L }[/math], there is 0 potential energy. Using the time-independent Schrodinger Equation with [math]\displaystyle{ V(x) = 0 }[/math], we arrive at the following Schrodinger Equation: [math]\displaystyle{ -\frac{\hbar^2}{2m}\frac{\partial^2\psi(x)}{\partial x^2}= E \psi(x) }[/math]
Isolating the second partial derivative term gives us the following: [math]\displaystyle{ \frac{\partial^2\psi(x)}{\partial x^2}= -\frac{2mE}{\hbar^2}\psi(x) }[/math]
To simplify this, let us define the constant k as the following: [math]\displaystyle{ k = \frac{\sqrt{2mE}}{\hbar} }[/math]
Rewriting the Schrodinger Equation with the constant k gives us [math]\displaystyle{ \frac{\partial^2\psi(x)}{\partial x^2} + k^2\psi(x) = 0 }[/math]
The general solution to this partial differential equation is very well known and is given here: [math]\displaystyle{ \psi(x) = Asin(kx) + Bcos(kx) }[/math]
We will now begin to solve for the constants A and B. Recall that we have imposed the boundary conditions of the probability of finding the particle to be 0 anywhere outside of [math]\displaystyle{ x = 0 }[/math] to [math]\displaystyle{ x = L }[/math]. This means that the wave function has to be continuous at the boundary.
First, consider the point [math]\displaystyle{ x = 0 }[/math]. Here, [math]\displaystyle{ \psi(0) = 0 }[/math]. For this to be true, we need to let B = 0. This is because [math]\displaystyle{ sin(0) = 0 }[/math], but [math]\displaystyle{ cos(0) = 1 }[/math]. If the [math]\displaystyle{ Bcos(kx) }[/math] term exists in our [math]\displaystyle{ \psi(x) }[/math], then our wave function would not be cointinuous at the point [math]\displaystyle{ x = 0 }[/math].
Next, consider the point [math]\displaystyle{ x = L }[/math]. Here, [math]\displaystyle{ \psi(L) = 0 }[/math]. For this to be true, [math]\displaystyle{ sin(kL) = 0 }[/math] when [math]\displaystyle{ ka = n\pi }[/math]. This is due to the nature of the sin function itself. This means that we can derive the following expression for k:
[math]\displaystyle{ k = \frac{n\pi}{L} }[/math]
Since we are only considering the case where the potentials are infinite at the barriers, we do not need to check for the derivatives of the wave function to be 0. If this were not an infinite potential well, then we would also have to take derivates of the wave function at each point and apply the boundary conditions to allow them to equal 0 as well.
Lastly, we will consider a normalization condition to solve for the constant A. If there is a 0% chance of finding the particle outside the well, then that must be there is a 100% chance of finding the particle somewhere within the well. This condition is expressed mathematically as
[math]\displaystyle{ \int_{0}^{L}\psi(x)^*\psi(x)dx=1 }[/math]
Since [math]\displaystyle{ \psi(x) }[/math] is a real function, we can rewrite the integrand as [math]\displaystyle{ \psi(x)^2 }[/math]. We can then solve for A by doing the following steps:
[math]\displaystyle{ \int_{0}^{L}\psi(x)^2dx=1 }[/math]
[math]\displaystyle{ A^2\int_{0}^{L}sin^2(kx)dx=1 }[/math]
Use the following identity: [math]\displaystyle{ sin^2(\theta) = \frac{1-cos(2\theta)}{2} }[/math]
[math]\displaystyle{ A^2\int_{0}^{L}\frac{1-cos(2\theta)}{2}dx=1 }[/math]
[math]\displaystyle{ A^2(\frac{L}{2} - \frac{sin(2kL}{4k}) = 1 }[/math]
Recall [math]\displaystyle{ kL = n\pi }[/math]
This means that [math]\displaystyle{ \frac{sin(2n\pi)}{4k} = 0 }[/math]
Therefore [math]\displaystyle{ A = \sqrt{\frac{2}{L}} }[/math]
Putting it all together, we arrive at the following wave equation: [math]\displaystyle{ \psi(x) = \sqrt{\frac{2}{a}}sin(\frac{n\pi}{a}x) }[/math]
Each associated wave function has corresponding energy to it. This can be solved by recalling our original definition of k.
[math]\displaystyle{ k^2 = \frac{2mE}{\hbar^2} }[/math]
[math]\displaystyle{ E = \frac{\hbar^2k^2}{2m} = \frac{\hbar^2n^2\pi^2}{2mL^2} }[/math]
We have now solved the particle in a 1-Dimensional box given our initial conditions mathematically!
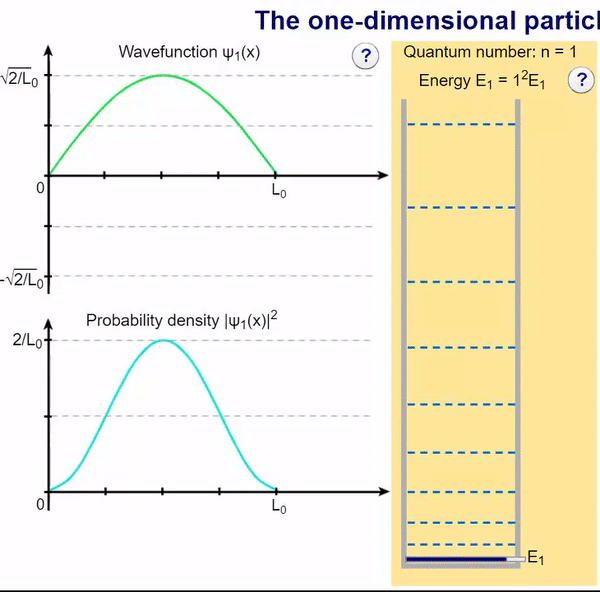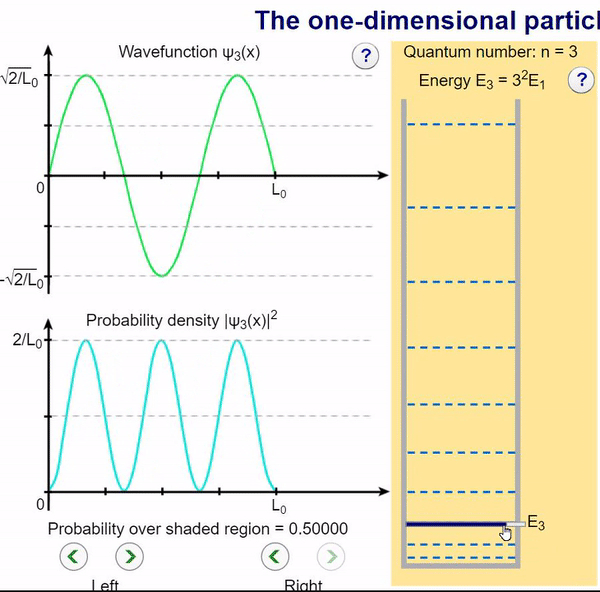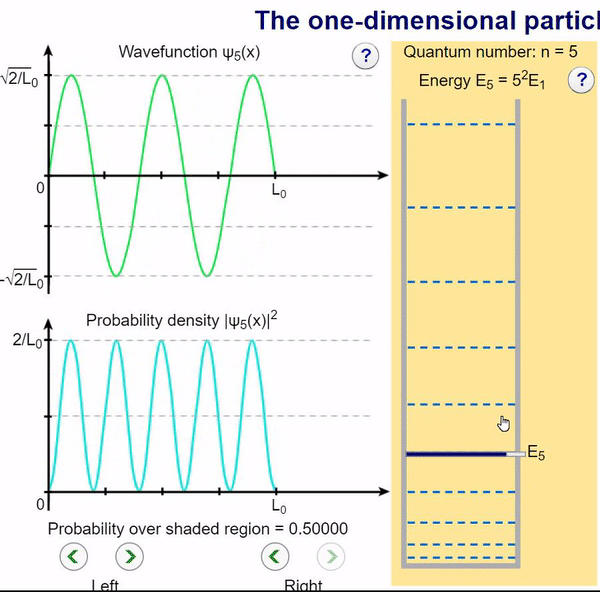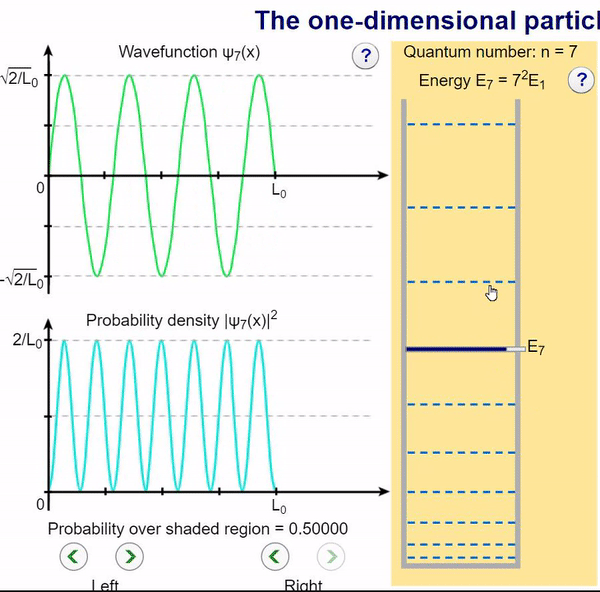
Infinite Potential (Computational Model)
Here, we can visualize the wave function and its associated probability density for various quantum levels. As you can see, the wave function changes depending on the quantum number and showcases interesting properties regarding its probability density. For quantum numbers greater than 1, there are places in which you are unable to find the particle within the boundary of the well, despite there being 0 potential energy!
Semi-Infinite Potential (Mathematical Model)
Next, let us consider the case where the boundary at [math]\displaystyle{ x = L }[/math] is no longer infinite, but a constant value V. In this case, we can again solve for the wave function with the Schrodinger Equation, except that we will now have a non-zero term for the potential. The solution to the Schrodinger Equation is as follows:
[math]\displaystyle{ -\frac{\hbar^2}{2m}\frac{\partial^2\psi(x)}{\partial x^2} + V\psi(x)= E \psi(x) }[/math]
[math]\displaystyle{ \frac{\partial^2\psi(x)}{\partial x^2}= -\frac{\hbar^2}{2m}(V-E)\psi(x) }[/math]
There are 2 cases to consider at this point, [math]\displaystyle{ V \lt E }[/math] and [math]\displaystyle{ V \gt E }[/math]
Again, using the fact that [math]\displaystyle{ k = \frac{\sqrt{2m(E \pm V)}}{\hbar} }[/math], we arrive at 2 following possibilities for the wave function
V < E [math]\displaystyle{ \psi(x) = Acos(kx) + Bsin(kx) }[/math]
V > E [math]\displaystyle{ \psi(x) = Ae^{kx}+Be^{-kx} }[/math]
From this point onwards, let us assume that V > E. This means that the following piecewise function defines our wave function for the following regions:
[math]\displaystyle{ \psi(x) = \left\{ \begin{array}{cl} 0 & : \ x \leq 0 \\ Acos(kx)+Bsin(kx) & : \ 0 \lt x \lt L \\ Ce^{-kx} & : x \geq L \end{array} \right. }[/math]
Solving for the constant terms in this wave function would require similar steps to that of the infinite potential: imposing boundary conditions while making sure the function is continuous and utilizing normalization conditions. These are merely mathematical footnotes for this article, and thus we will be skipping over them. However, we will take a closer look at what happens when [math]\displaystyle{ x \geq L }[/math].
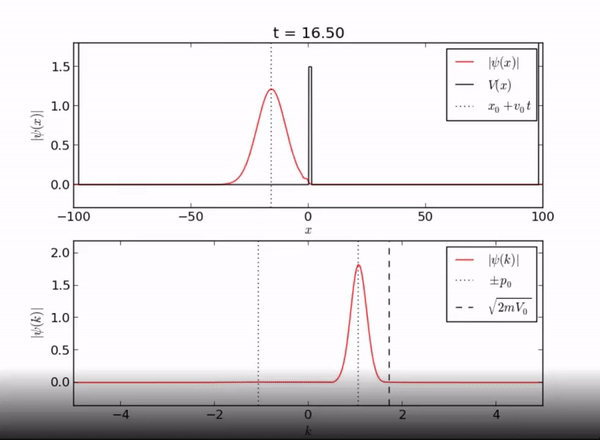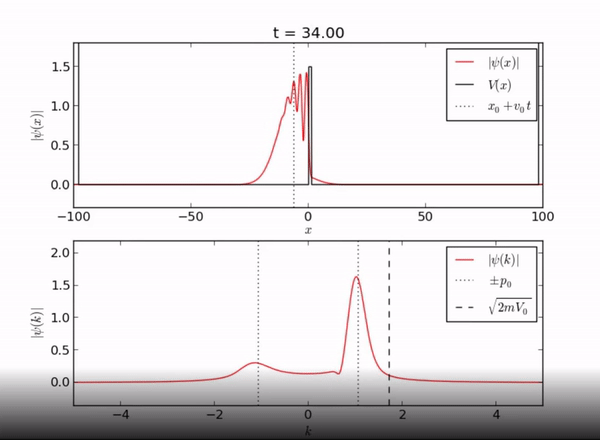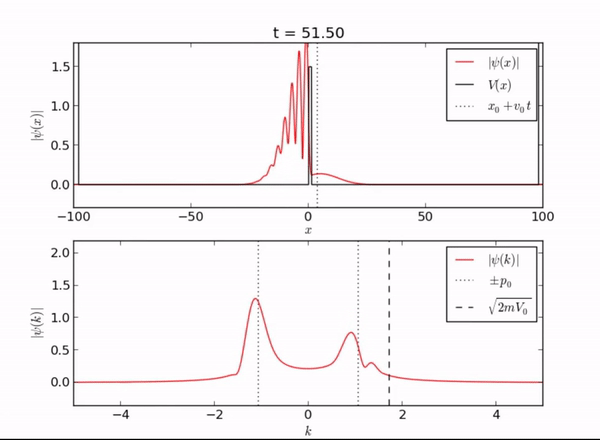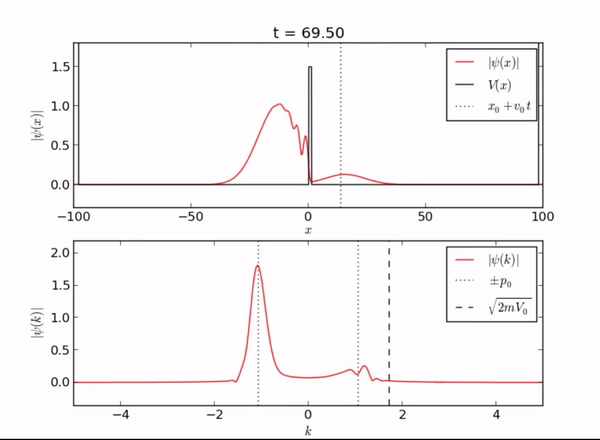
Classically, if a particle encounters a barrier and does not have sufficient energy to overcome the potential, it will not be allowed to pass through the barrier. However, in this quantum system, the particle can be found outside of the well! As you can see from the piecewise function above, the associated wave function is a decaying exponential. This is the basis of quantum tunneling, whereby a particle can pass through a forbidden region.
The distance a particle can penetrate is given by the following expression: [math]\displaystyle{ \delta x = \frac{h}{\sqrt{2m(V-E)}} }[/math]. As you can see, the penetration depth is proportional to Planck's constant, meaning that this distance will be very small.
Semi-Infinite Potential (Computational Mode)
Here we demonstrate the exponential behavior of the wave function as it enters [math]\displaystyle{ x \geq L }[/math]. As seen, the wave function can exist beyond the barrier due to quantum tunneling.
Examples
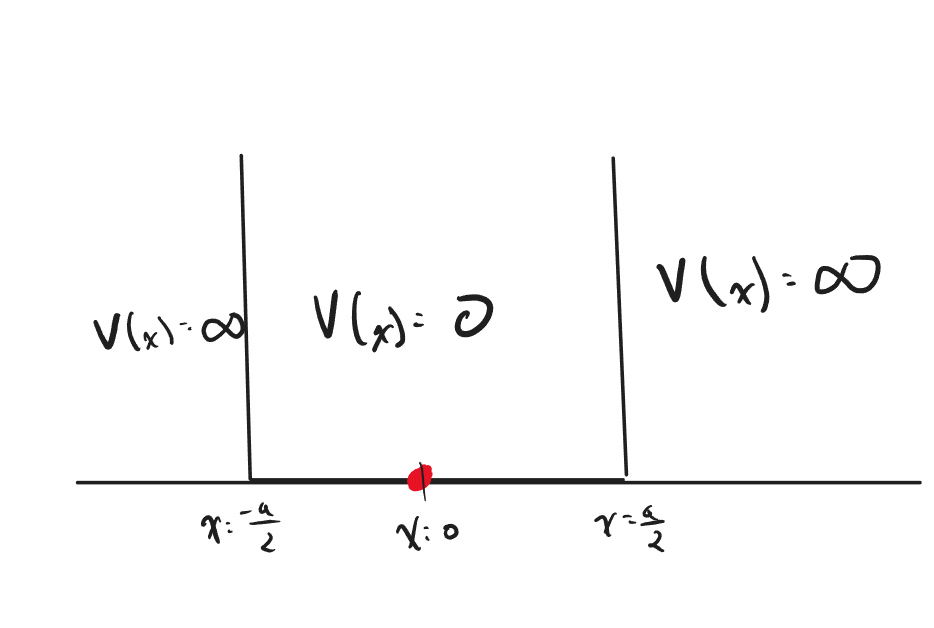
The General Infinite Potential Well
Consider the following quantum system as shown below
Determine the wave functions for this potential.
The solution to this problem is the exact same setup as the what was shown earlier in the infinite potential section, however we have shifted our coordinate system over such that the particle is bounded by [math]\displaystyle{ \pm\frac{a}{2} }[/math] on both sides. This small change will lead us to an even more general version of the wave function for this system.
To solve for the wave function [math]\displaystyle{ \psi(x) }[/math], begin with the time-independent Schrodinger Equation and the potential at the region of interest.
[math]\displaystyle{ -\frac{\hbar^2}{2m}\frac{\partial^2\psi(x)}{\partial x^2} = E \psi(x) }[/math]
[math]\displaystyle{ \psi(x) = Acos(kx) + Bsin(kx) }[/math]
Apply boundary conditions are [math]\displaystyle{ x = \pm\frac{a}{2} }[/math] such that [math]\displaystyle{ \psi(\pm\frac{a}{2}) = 0 }[/math]
[math]\displaystyle{ \psi(frac{a}{2}) = Acos(\frac{ka}{2}) + Bsin(\frac{ka}{2}) = 0 }[/math]
[math]\displaystyle{ \psi(-frac{a}{2}) = Acos(\frac{ka}{2}) - Bsin(\frac{ka}{2}) = 0 }[/math]
Adding these two wave functions together yields the following results: [math]\displaystyle{ 2Acos(\frac{ka}{2}) }[/math]. This implies that [math]\displaystyle{ k = \frac{2\pi(n + \frac{1}{2})}{a} }[/math].
Subtracting these two wave functions yields the following results: [math]\displaystyle{ 2Bsin(\frac{ka}{2}) }[/math]. This implies that [math]\displaystyle{ k = \frac{2\pi n}{a} }[/math].
We can keep both of these solutions if we allow the following piece-wise function to exist:
[math]\displaystyle{ \psi(x) = \left\{ \begin{array}{cl} Acos(\frac{\pi n}{a}x) & : \ for \hspace{2mm}odd\hspace{2mm}integers\\ Bsin(\frac{\pi n}{a}x) & : \ for \hspace{2mm}even\hspace{2mm}integers \end{array} \right. }[/math]
This is the more general solution for the infinite potential well as we now have both triginometric terms available in our wave function.
Connectedness
- How is this topic connected to something that you are interested in?
This topic of a particle in a 1-Dimensional Box is interesting to me since it shows the direct implications of Schrodinger's Equation. Being able to understand and solve what most consider a cornerstone for quantum physics is part of the reason why I love physics so much. Not only am I able to solve this equation for many different cases, but I'm also able to understand and interpret the results. I can see how the equation lends its way to how energy must be quantized, or how it directly implies Heisenberg's uncertainty principle.
- How is it connected to your major?
This topic of being able to solve a particle in a 1-Dimensional box is directly related to how I should approach, understand, and appreciate physics problems in the future. This idea lays the groundwork for future endeavors into Schrodinger's Equation when I take quantum mechanics later for my major.
- Is there an interesting industrial application?
While solving the equation itself does not lead to many interesting industrial applications, the solutions of Schrodinger's Equations lend their way to explaining quantum tunneling. Quantum tunneling can be applied in many different ways, including in Scanning-Tunneling Microscopes (STM), radioactive decay, and Potassium-Argon dating.
History
Erwin Schrodinger was born on August 12th, 1887 in Vienna. He would be most well known for his work in developing his namesake equation that provides a way to calculate the wave function of a quantum system and predict how it will evolve with time. He did this after scientist Peter Debye listened to a lecture given by Schrodinger concerning De Broglie's wave-particle duality theory. Debye did not agree with this De Broglie's theory since it showed the existence of matter waves, but not the equation for the wave itself. At the time, there was no equation whose solution would describe the waves created by De Broglie's theory. Erwin Schrodinger would dedicate his work to solving this problem, and by January 1926, he published his paper "Quantization as an Eigenvalue Problem" which displays his namesake equation. This paper correctly gave the energy values for a hydrogen atom for time-independent systems. Over the following year, he would publish more papers furthering his equation by solving the quantum harmonic oscillator among other accomplishments.
See also
External links
https://en.wikipedia.org/wiki/Erwin_Schr%C3%B6dinger#Quantum_mechanics
https://www.youtube.com/watch?v=2WPA1L9uJqo
https://www.st-andrews.ac.uk/physics/quvis/simulations_html5/sims/infwell1d/infwell1d.html
https://jakevdp.github.io/blog/2012/09/05/quantum-python/
References
Prof. Trebino's Schrodinger Equation Video
https://www.st-andrews.ac.uk/physics/quvis/simulations_html5/sims/infwell1d/infwell1d.html