Nuclear Fission

Claimed by Harrison Melton (Fall 2021). Nuclear fission is the process of splitting up an atom into multiple parts. This occurs spontaneously in the form of radioactive decay or artificially with the inclusion of neutrons into an environment of fissionable matter.

The Main Idea

Nuclear fission is the process of the nucleus of an atom splitting into multiple smaller parts and, in doing so, releasing a quantity of energy. This process can happen naturally in the form of radioactive decay or in a nuclear reaction. Nuclear fission by radioactive decay is a natural process whereby a nucleus that is very big and unstable spontaneously breaks apart into two or three smaller nuclei and emitting particles such as neurons and gamma radiation in the process. Radioactive decay is very uncommon amongst most large molecules but does happen naturally for Uranium-235 and Plutonium-239, both of which are isotopes. Uranium-235 fissions when gains extra neurons that trigger its decay. The two substituents that form from the split atom have a mass that is about one tenth of one percent less mass than that of the original atom. Nuclear fission by nuclear reaction occurs when one nucleus collides with either another nucleus or a particle causing the nucleus to break apart into other smaller nuclei and releasing particles and gamma radiation. This can cause chain reactions whereby particles emitted when one nucleus fissions go on to collide with other nuclei and cause them to fission which releases more particles that go on to collide with even more nuclei. Nuclear fission reactions are typically managed to produce a standard and controlled reaction (such as the process to produce electricity) but when it is not managed it results in a dangerous and uncontrollable release of energy (such as the atomic bomb).

Microscopic/Macroscopic Cross Section

The probability that fission will occur at all is dependent on the Microscopic Cross Section(σ) of fission for the particular atom. The Microscopic Cross Section is the area, in barns, that an interaction can occur. An incident neutron will have to hit the atom within this Cross Section for fission, absorption, scattering, or another interaction to occur. A particular atom has a total cross section that is determined by the equation:

[math]\displaystyle{ σt = σs + σi + σγ + σf }[/math]

The variables are as follows:

- Total cross-section (σt)
- elastic scattering cross-section (σs)
- inelastic scattering cross-section (σi)
- absorption cross-section (σa)
- radiative capture cross-section (σγ)
- fission cross-section (σf)

If a neutron was to interact with a number of atoms, the resulting cross section of all of the atoms is the Macroscopic Cross Section(Σ). The Macroscopic Cross Section is found by taking the total cross section of the atom and multiply it by the atomic density of whatever volume of atoms you desire to interact with. The formula for the Macroscopic Cross Section is as follows:

[math]\displaystyle{ \Sigma = \sigma * N }[/math]

Q-Value

The quantity of energy that is released during a reaction is dependent, at it's core, on the equation [math]\displaystyle{ E = mc^2 }[/math]. More specifically, the energy gained or lost in a reaction is known as the Q-Value and is found using the equation:

[math]\displaystyle{ Q = (Kinetic Energy: initial) - (Kinetic Energy: Final) = c^2(rest mass: initial - rest mass: final) }[/math]

Therefore, if you had a reaction [math]\displaystyle{ x + X = Y + y, Q = c^2(m(x) + m(X) - m(Y) - m(y)) }[/math].

Often, when working with amu(atomic mass units), we can replace [math]\displaystyle{ c^2 }[/math] with the equivalent 931.5 MeV/amu.

A Computational Model

Examples

What is the Q-Value of a Deuterium-Deuterium Fusion Reaction(D(D,n)3-HE)? Lets first evaluate the masses of each atom in amu. This is normally given to you either in a reference sheet or in the problem itself.

[math]\displaystyle{ m(D) = 2.014102 amu }[/math]

[math]\displaystyle{ m(n) = 1.008665 amu }[/math]

[math]\displaystyle{ m(3-He) = 3.0160293 amu }[/math]

Now we will use the formula given above to solve for Q. Don't forget to put [math]\displaystyle{ 931.5 MeV/amu }[/math] in place of [math]\displaystyle{ c^2 }[/math].

[math]\displaystyle{ Q = c^2(2*m(D) - m(n) - m(He) }[/math]

[math]\displaystyle{ Q = 931.5 Mev/amu*(2(2.014102 amu) - 1.008665 amu - 3.0160293 amu) }[/math]

[math]\displaystyle{ Q = 3.2693 MeV }[/math]

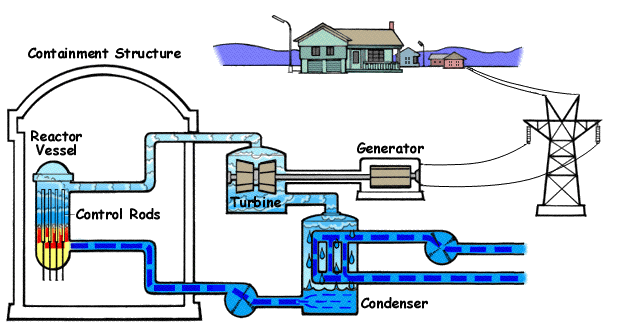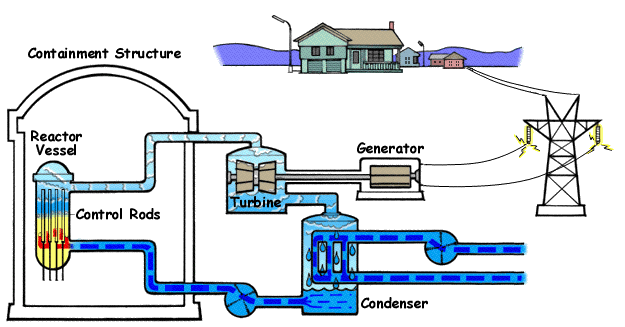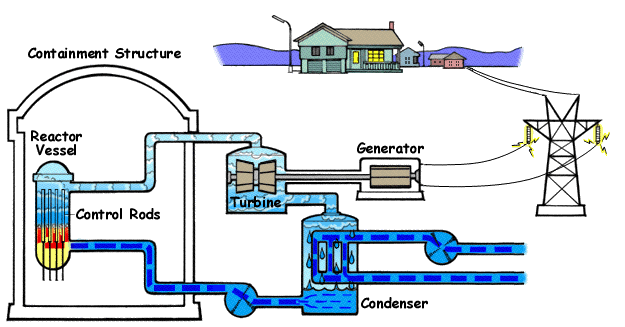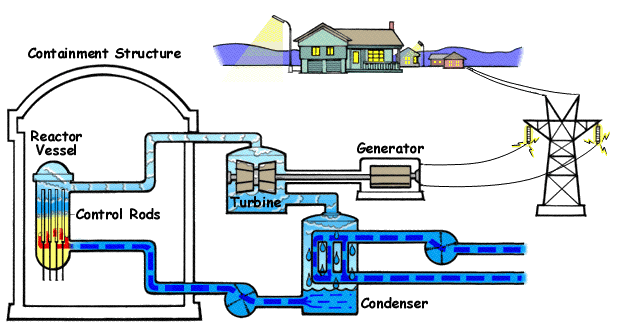
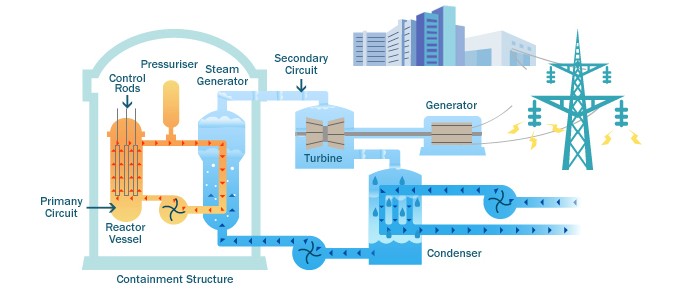
Nuclear power plants like these are found in various countries all over the globe. They work by heating water to boiling with nuclear fission. The water turns to steam and turns turbines, generating electricity.

Below is a diagram illustrating a BWR(Boiling Water Reactor) and how they generate electricity with nuclear fission and water.

Below is a diagram illustrating a PWR(Pressurized Water Reactor) and how they generate electricity with nuclear fission and water.

Connectedness

Nuclear fission is a very interesting topic to me because of its potential for green and renewable energy. After delving deeper into the subject, I was made aware of just how astonishingly large the amount of energy that is produced from the splitting of an atom actually was. I was always aware of what nuclear fission was because of its use in the atomic bomb and the basic explanation in secondary school. This topic however does not directly tie into my major of Biomedical engineering. The results of effective nuclear fission would be energy with which to power some types of biomedical devices as well as the potential to learn more about elements and materials that could be used in nuclear fission and other things. The overall industrial application of nuclear fission is actually quite impressive, it has the potential to be one of the most reliable and consistent forms of power production once the remainder of fossil fuels are depleted. Nuclear fission is a growing form of producing energy and will become an even better alternative once there is an adequate way to dispose of the radioactive waste that it produces.

History

In 1896, French physicist Henri Becquerel noticed that uranium fluoresces under UV light and conducts experiments to examine this phenomena. Among the most famous of these experiments is one involving a clear piece of photographic film wrapped in black paper. A piece of uranium is placed on top of the wrapped film and left in the sunlight. When unwrapped, Becquerel finds that the clear film has become foggy. He believed that the uranium absorbs the sunlight and releases invisible ray that penetrate the paper and dye the film. However, upon further investigation, Becquerel is baffled to find that the uranium dyes the film even when placed in the drawer without any light. This must mean that some form of energy comes from inside the uranium. Ernest Rutherford and Frederick Soddy take to studying uranium on a quantum level. They discover that this element has a large nucleus that is so unstable, it spits out small pieces of itself containing protons, thereby becoming a completely different element. They watch uranium transform into Thorium. The thorium, also radioactive becomes Protactinium. This continues for fourteen different elements, the last of which being lead. A student of Rutherford, Otto Hahn, experiments with forcing uranium to change. Hahn and his assistant discover that it is actually possible to split the nucleus of the uranium atom. Together they discover that only uranium-235 will split. With 235 protons and neutrons, the nucleus is so huge and under so much strain, adding just one neutron makes the nucleus so unstable it causes the nucleus to fission. Hahn won the Nobel Prize in 1945 for discovering chemical proof of nuclear fission.

Soon after the discovery of Hahn and his assistant, in a basement at the University of Chicago, Enrico Fermi and his team developed the first nuclear reactor. Their experiment, being the first chain reaction of a fissile material, took advantage of the use of moderators to slow the neutrons, thus increasing the probability that fission will occur.

Fission Weapons

Nuclear fission's potential to release large amounts of energy was inevitably utilized for the creation of powerful weaponry by atomic scientists. The bombs created by this process are referred to as nuclear bombs. While development of these weapons still persists today, these weapons have been deployed only twice, with both instances occurring during the Second World War.

The first and only atom bombs to be deployed were both developed in the mid-1900s. These weapons were given the nicknames of "Little Boy" and "Fat Man". While both American-made, these two weapons were distinct from each other in both their chosen "nuclear fuel" and their overall design concept. While there are several elements that can undergo nuclear fission, the most commonly used are Uranium-235 and Plutonium-239. These uranium and plutonium isotopes were the chosen fuel of the Little Boy and Fat Man bombs respectively. To detonate, in both cases, the nuclear mass within the bomb would have to reach a point of critical mass. Reaching critical mass effectively required unique approaches for the different elements.

For the Uraninum-235 to reach critical mass in the Little Boy bomb, a collision method was used. The process involved two smaller amounts of Uranium-235, initially set apart from each other. To then reach critical mass, one set of Uranium-235 was fired at the other, setting off a chain-reaction. The reason why this approach couldn't be used for the Plutonium-239-based Fat Man bomb was due to the higher fission rate of the Plutonium-239. The collision method was unable to combine the masses quickly enough. Instead, scientists relied on the proportional relationship between density and mass, mass being the product of density and volume. In the Fat Man bomb, explosives were placed around the Plutonium-239 to allow for rapid compression.

http://www.world-nuclear.org/
http://www.nuclear-power.net/nuclear-power/reactor-physics/nuclear-engineering-fundamentals/neutron-nuclear-reactions/atomic-number-density/

Nuclear Fission

Contents

The Main Idea

A Computational Model

Examples

Connectedness

History

Fission Weapons

See also

Further reading

References

Navigation menu