Multi-particle analysis of Momentum
The Main Idea
Newton's third law states (on a basic level) that for every action, there is an equal and opposite reaction. The application and importance of this law in terms of momentum is that in a "closed system," momentum is conserved. The meaning of "closed" is that within the system--the actions and reactions on the involved objects--all forces are accounted for. We can model conservation of momentum by looking at the bodies of a system as particles, which is what will be discussed for the remainder of this article. The momentum principle and the multi-particle analysis of it make it easier to analyze situations such as collisions, and can make it much easier to solve problems.
A multi-particle analysis of momentum can be applied to systems with multiple objects that may be interacting. Using the same principles of momentum applied on single objects, we apply these on the multiple objects that may make up a chosen system. However, one interesting characteristic of the multi-particle analysis of momentum is that it only factors in external forces applied on the object as opposed to internal forces which would be applied by objects on one another within a system even though objects within the system are interacting.
Multi-particle System Momentum Principle
[math]\displaystyle{ ∆\vec{p} = \vec{F}_{net} * {∆t} }[/math]
Where Fnet is the sum of all external forces on the system. Therefore:
[math]\displaystyle{ \vec{F}_{net} = \vec{F}_{1} + \vec{F}_{2} + \vec{F}_{3} + ... }[/math]
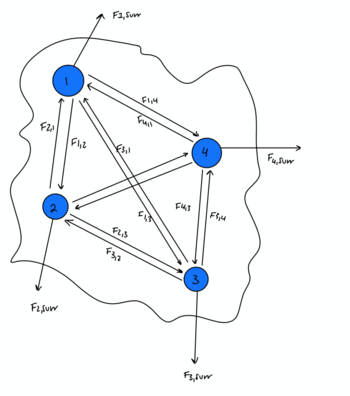
Note: Figure created by author
From the figure above, we can see that there are internal forces within the system since each object contributes a force to its surrounding objects. However, when applying the multi-particle momentum principle, we only look at the external forces. So in this case, to sum the forces in order to find the change in momentum we would add F1,surr + F2,surr + F3,surr + F4,surr to sum up to an Ftotal that we would multiply by the time elapsed in order to determine the change in momentum.
The reason that the internal forces are not used within the momentum principle is because the internal forces would cancel due to the principle of reciprocity. Since each object exerts an equal and opposite force on each other, all of the internal forces would cancel, leaving only the external forces. This makes solving the momentum for the system, which would have been a complicated to solve for with a multitude of forces, much simpler.
Theory of reciprocity results in this:
[math]\displaystyle{ \vec{F}_{1,2} = \vec{-F}_{2,1} }[/math]
[math]\displaystyle{ \vec{F}_{1,3} = \vec{-F}_{3,1} }[/math]
[math]\displaystyle{ \vec{F}_{1,4} = \vec{-F}_{1,1} }[/math]
And this would be the case for every object in the system (objects 2,3 and 4).
More on Proving the Cancellation of Internal Forces:
Where p is momentum, F is the net force from the surroundings, and t is time, measured in seconds, The Momentum Principle is formulaically defined as
[math]\displaystyle{ {\frac{d\vec{p}}{dt}}_{system}= \vec{F}_{net} }[/math] (or [math]\displaystyle{ ∆\vec{p} = \vec{F}_{net} * {∆t} }[/math]).
Taking two particles, particle 1 and particle 2, we can define the total momentum as:
[math]\displaystyle{ P = p_1 + p_2 = m_1v_1 + m_2v_2 }[/math]
and deriving from [math]\displaystyle{ F = m * a }[/math], the rate of change is the sum of the vector forces, and therefore:
[math]\displaystyle{ \frac{d\vec{P}}{dt} = m_1\vec{a}_1 + m_2\vec{a}_2 }[/math].
Newton's third law gives that:
[math]\displaystyle{ \frac{d\vec{P}}{dt} = 0 }[/math],
so,
[math]\displaystyle{ m_1\vec{a}\_1 + m_2\vec{a}_2 = 0 }[/math].
[math]\displaystyle{ \vec{F}_{12} = -\vec{F}_{21} }[/math].
[math]\displaystyle{ \vec{F}_{12} = m_2\vec{a}_2 }[/math].
The total momentum does not change despite the particles' change in position, velocity, and acceleration. This does not mean that each individual particle will retain the same momentum, but that the total momentum of the system is conserved.
If i and j are the first two particles out of total N particles,
[math]\displaystyle{ \vec{P} = \sum_{i=1}^N m_i\vec{v}_i }[/math] and [math]\displaystyle{ \frac{d\vec{P}}{dt} = \sum_{j=1}^N m_j\vec{a}_j = \sum_{j=1}^N\sum_{i=1}^N F_{ij} }[/math].
Each term in this sum cancels with another due to the application of "equal and opposite."
If the system is subject to a force that is not included in the system (external),
[math]\displaystyle{ \frac{d\vec{P}}{dt} =\vec{F}_{ext} }[/math].
See more on that at: [1]
A Mathematical Model
Mathematically, momentum is the product of a system's mass and the change in its velocity. It is also defined as the product of the net force on the system and the time in which the force was applied. This principle stays the same for a multi-particle system and for a multi-particle system we would define the momentum as this:
[math]\displaystyle{ \vec{p}_{sys}= \vec{p}_{1} + \vec{p}_{2} + \vec{p}_{3} }[/math]
And for a multi-particle system, since internal forces cancel, to find the total force on on the system, we add only the external forces applied to each object within the system:
And use the sum of the forces in the following equation:
[math]\displaystyle{ \vec{∆p}_{sys} = \vec{F}_{net,surr} * ∆t }[/math]
This equation can essentially be broken down further into this:
[math]\displaystyle{ \vec{∆p}_{1} + \vec{∆p}_{2} + \vec{∆p}_{3} = (\vec{F}_{1,surr} + \vec{F}_{2,surr} + \vec{F}_{3,surr}) * ∆t }[/math]
Computational Models
Click on the link below to understand the basics of the momentum principle in VPython,
# GlowScript 1.1 VPython
#people
#note that the people has a trail
human1=sphere(pos=vec(-40,0,0), radius=0.5, color=color.red, make_trail=true)
human2=sphere(pos=vec(-20,0,0), radius=0.5, color=color.green, make_trail=true)
human3=sphere(pos=vec(20,0,0), radius=0.5, color=color.blue, make_trail=true)
human4=sphere(pos=vec(40,0,0), radius=0.5, color=color.white, make_trail=true)
human1.m=0.1 #mass of the people in kg
human2.m=0.1
human3.m=0.1
human4.m=0.1
human1.p=human1.m*vec(0,0,0) #starting momentum mass times velocity
human2.p=human2.m*vec(-2,0,0)
human3.p=human3.m*vec(0,2,0)
human4.p=human4.m*vec(-2,2,0)
t=0
dt=0.01 #size of the time step
#putting the loop as "while True" means it runs forever
#you could change this to while t< 10: or something
while t<0.02:
rate(100) #this says 100 calculations per second
#given net force
Fnet=vec(1,-6,-1)
#update the momentum
human1.p=human1.p+Fnet*dt
human2.p=human2.p+Fnet*dt
human3.p=human3.p+Fnet*dt
human4.p=human4.p+Fnet*dt
#update the position of the ball
human1.pos= human1.pos +human1.p*dt/human1.m
human2.pos= human2.pos +human2.p*dt/human2.m
human3.pos= human3.pos +human3.p*dt/human3.m
human4.pos= human4.pos +human4.p*dt/human4.m
#this next line updates the spring
#spring.axis=ball.pos-holder.pos
print("Final Momentum of Human 1 = ",human1.p," kg*m/s")
print("Final Momentum of Human 2 = ",human2.p," kg*m/s")
print("Final Momentum of Human 3 = ",human3.p," kg*m/s")
print("Final Momentum of Human 4 = ",human4.p," kg*m/s")
or check out this collision simulation to see a multi-particle analysis of it:
Examples
Simple
A loaded cart is travelling with momentum Mcart, and a brick is falling with momentum Mbrick. As the cart advances forward, the brick lands on it and the now heavier cart continues to move forward. The initial momentum of the system includes that of the cart and of the brick. Symbolically, what is the final momentum of the system?
Answer: Mcart + Mbrick
Explanation:
As explained through the mathematical and computational models above, Newton's Third Law allows us to assume that momentum is conserved within the system before and after a collision, meaning that the initial and final momentum of the system are the same. The initial momentum here is Mcart + Mbrick, therefore the final momentum is the same.
Middle
Given a car with a mass of 200kg and an initial velocity of 90m/s and a truck with a mass of 950kg and an initial velocity of 80m/s, find the TOTAL, FINAL momentum of the system after the car and truck collide. Include both the car and truck in the system.
Answer: 9.4e4 N
Explanation:
With the car as particle 1 and the truck as particle 2, total initial momentum = [math]\displaystyle{ p_1 + p_2 = m_1v_1 + m_2v_2 }[/math]
Initial momentum = Final momentum, therefore total final momentum = [math]\displaystyle{ p_1 + p_2 = m_1v_1 + m_2v_2 }[/math], which is equal to 9.4e4N.
Difficult
A woman, Katherine, and a man, Robert, each have a mass of [math]\displaystyle{ {m_{people}} }[/math], and decide to have some fun in the theatre before putting away curtains. They stand on top of a curtain bin with mass [math]\displaystyle{ {m_{bin}} }[/math]. Katherine and Robert jump off of one side of the bin at a velocity of v relative to the bin, and when they do so, the bin rolls in the direction opposite of which they jumped. Symbolically, what is the final velocity of the bin if both Katherine and Robert jump at the same time?
Answer: [math]\displaystyle{ v_f = \frac{2m_{people} * v}{m_{people} + m_{bin}} }[/math]
Explanation: Momentum before: 0, Momentum after: [math]\displaystyle{ (2m(v - v_f) - m_{bin} * v_f) * i }[/math] so, [math]\displaystyle{ 0 = 2m_{people}(v - v_f) - m_{bin} * v }[/math]
Then solve for [math]\displaystyle{ v_f }[/math].
Connectedness
Multi-particle analysis of momentum is just one way of analyzing a particular system, but multi-particle analysis is a way to examine other systems as well, and the momentum principle is very important for a variety of professional fields.
One application includes its use by automobile safety engineers, who must take into account the physics of momentum in order to safely design vehicles for their customers' use. However, this is by no means the only application--momentum is an applicable concept for literally anything that moves and has mass: figure skaters, roller coasters, pool balls...the list goes on.
For computer scientists, it's possible to create simulations like those listed in the "Computational Models" section of this article! In order to design those it is necessary for the creator to understand not only computer science concepts, but also the physics concepts that they are attempting to represent. In any field, it is possible that momentum comes into play.
History
The scientists most credited for the introduction of the concept of momentum to their field are Rene Descartes and Isaac Newton. Newton is more acknowledged for his Laws, from which the more specific concept of Conservation of Momentum can be derived, while Descartes holds the original "discovery" of momentum.
More information on the history of momentum can be found at: [2] and [3]
See also
In order to better understand the multi-particle analysis of Momentum, it would be best to first visit: Momentum Principle
and to then explore the Conservation of Momentum page: [4].
Other information on multi-particle systems can be found in the Week 9 category of the Main Page: Main Page.
Check out the links in the references below for more information on this subject as well as other physics concepts!
References
[1] Fitzpatrick, R. (2006, February 2). Angular momentum of a point particle. Retrieved November 27, 2016, from http://farside.ph.utexas.edu/teaching/301/lectures/node118.html
[2] Torre, Charles. "Newton's Third Law. Multi-Particle Systems." Newton’s Third Law. Multi-particle Systems. Conservation of Momentum. Physics 3550, Fall 2012 Newton’s Third Law. Multi-particle Systems. Relevant Sections in Text: §1.5, 3.1, 3.2, 3.3 (2012): n. pag. Intermediate Classical Mechanics. Utah State University, Sept. 2012. Web. 27 Nov. 2016.
[3] Harris, William. "How Netwon's Laws of Motion Works." HowStuffWorks. HowStuffWorks.com, 29 July 2008. Web. 27 Nov. 2016. <http://science.howstuffworks.com/innovation/scientific-experiments/newton-law-of-motion.htm>
[4] Sherwood, Bruce A. "2.1 The Momentum Principle." Matter & Interactions. By Ruth W. Chabay. 4th ed. Vol. 1. N.p.: John Wiley & Sons, 2015. 45-50. Print. Modern Mechanics.
[5] Fenton, Flavio. "Momentum and Second Newton's Law." 27 Nov. 2016. Lecture.
[6] Henderson, Tom. "Momentum and Its Conservation." Momentum and Its Conservation. The Physics Clasroom, 31 Dec. 2012. Web. 27 Nov. 2016.
[7] Dourmashkin, Peter. Lister, J. David. Pritchard, David E. Surrow, Bernd. "Momentum and Collisions." Massachusetts Institute of Technology. Sep. 2004. Lecture.