Mechanical Waves
Claimed by Snehil Mathur (Spring 2022)
Mechanical Waves are waves that propagate through a medium, one that is either solid, liquid, or gas. The speed at which a wave travels depends on the mediums' properties, both elastic and inertial.
The Main Idea
Waves can be described as disturbances that travel through space and can transport energy from its source to another location. These are often represented in an oscillating manner.
Mechanical waves are waves that propagate through matter (gas, liquid, or solid) and require a medium in order to transport energy. Inherently, these waves cannot travel through a vacuum.
There are three main types of mechanical waves:
Transverse Waves:
Waves in which the particles oscillate back and forth in the direction perpendicular to the motion of the wave. The particle travels the length of the amplitude of the and completes its oscillation corresponding to when the wave moves over one wavelength. Some examples of transverse waves are ripples in the water and a vibrating string.
Longitudinal Waves:
Waves in which the particles move in the same direction as the wave motion. While still in an oscillating motion, they move "back-and-forth" with respect to the direction the wave is propagating in. Some examples of longitudinal waves include sound waves and the motion of compressing and stretching a spring.
Surface Waves:
Waves in which the particles within the medium move both parallel and perpendicular to the propagation direction of the wave. They're called surface waves due to their nature of travelling along the surface of a medium. This gives the particles on the wave a circular-like motion. The surface of a wave in the water is the most direct example of a surface wave; other examples include seismic waves and gravity waves along the surface of liquids.
A Mathematical Model
Mechanical waves implement a variety of equations that can be used to solve for different characteristics of a wave. The wave equation is used to find the speed of propagation of a transverse wave:
[math]\displaystyle{ v = \lambda f }[/math]
Where [math]\displaystyle{ v }[/math] is the velocity, [math]\displaystyle{ \lambda }[/math] is the wavelength, and [math]\displaystyle{ v }[/math] is the frequency. Another form of this equation specific to mechanical waves is the formula:
[math]\displaystyle{ v = \sqrt{Stiffness/Inertia} }[/math]
Another common form of this equation is the wave speed for a stretched string, [math]\displaystyle{ v = \sqrt{T/\mu} }[/math], where [math]\displaystyle{ T }[/math] is the string tension and [math]\displaystyle{ \mu }[/math] is the mass per unit length of string. This equation allows for the calculation of the speed of a wave in different forms of matter. To find the equation of a wave that falls under two different mediums, we can apply superposition to find the new wave equation by adding the functions the two different functions that describe possible waves in the medium:
[math]\displaystyle{ y(x,t)=y_{1}+y_{2} }[/math]
Where [math]\displaystyle{ y_{1} }[/math] and [math]\displaystyle{ y_{2} }[/math] are the two possible wave functions for different mediums.
A Computational Model
How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript
Examples
Simple
Q1) What kind of wave is a stadium wave?
A1) Transverse Wave
Middling
Q2)
A wave travels with a period of 5 ns. The wave can be seen in the image below:
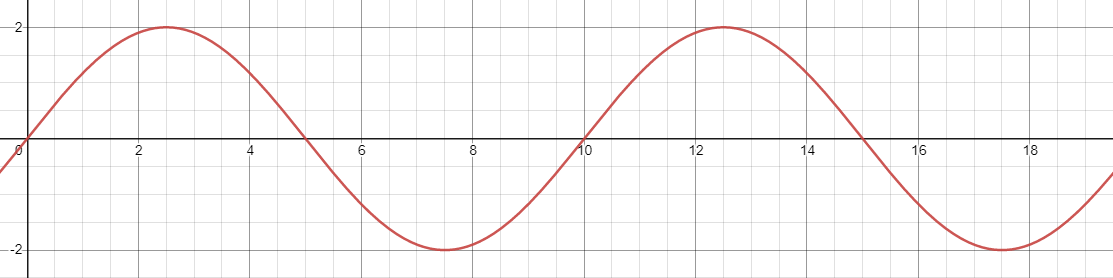
(The units of both of axis of this graph are in nm)
Find the speed of the wave described above:
A2) The wave equation to find the speed of this function is: [math]\displaystyle{ v = \lambda f }[/math]. To find the frequency, we apply the conversion from period to frequency: [math]\displaystyle{ f=1/T }[/math]
[math]\displaystyle{ f=\frac{1}{5*10^{-9}} = 2*10^8 }[/math]
To find the wavelength [math]\displaystyle{ \lambda }[/math], we find the length it takes for the wave to complete on cycle. Based on the graph, we can visually verify that the wavelength is 10 nm. With both the wavelength and the frequency, we can calculate the speed:
[math]\displaystyle{ v = (2*10^9)(10*10^9) = \textbf{2*10^19} }[/math]
Difficult
Q3) A transverse wave moves across a string. The wave can be represented with the equation [math]\displaystyle{ y(x,t)=0.5*sin(7x-3t) }[/math] with respect to it's position [math]\displaystyle{ x }[/math] in meters and time [math]\displaystyle{ t }[/math] in seconds. Find the amplitude, wavelength, period, and speed of the wave.
A3) For this question, we can use a lot of the wave functions we've learned from the past in order to convert the constants in this equation to the characteristics needed. First, we can write this equation as a form of its parent function:
[math]\displaystyle{ y(x,t)=Asin(kx-\omega t) }[/math]
Where [math]\displaystyle{ A }[/math] is the amplitude, [math]\displaystyle{ k }[/math] is the wave number, and [math]\displaystyle{ \omega }[/math] is the angular frequency. From reading the given equation, we can find:
[math]\displaystyle{ \textbf{Amplitude = 0.5 m} }[/math]
[math]\displaystyle{ k = 7 }[/math]
[math]\displaystyle{ \omega =3 }[/math]
We can use the wave number [math]\displaystyle{ k }[/math] to find the wavelength:
[math]\displaystyle{ k=\frac{2\pi}{\lambda} }[/math]
[math]\displaystyle{ \textbf{Wavelength = λ}=\frac{2\pi}{k}≈\textbf{0.898 m} }[/math]
To find the period [math]\displaystyle{ T }[/math], we convert from the angular frequency with this equation:
[math]\displaystyle{ \omega =\frac{2\pi}{T} }[/math]
[math]\displaystyle{ \textbf{Period = T = }=\frac{2\pi}{\omega}≈\textbf{2.094 s} }[/math]
Finally, to find the speed, we can an altered version of the wave equation to substitute in [math]\displaystyle{ k }[/math] in order to make it easier:
[math]\displaystyle{ v=\frac{\omega}{k} }[/math]
[math]\displaystyle{ =\frac{3}{7}≈0.429 }[/math]
[math]\displaystyle{ \textbf{Speed = v ≈ 0.429} }[/math]
Connectedness
- This topic is connected to the way sound moves. They're created by an object vibrating and generating pulses of pressure waves that travel through the air and carry energy over distances.
History
- Wasn't able to find directly related information to mechanical waves
See also
Connected topics include Electromagnetic Waves and Spring Motion.
Further reading
From cK-12.org: [4]
From Texas A&M University: [5]
External links
References
This section contains the the references you used while writing this page