Lenz's Law
Claimed by Lucia Jang, Fall 2025
The Main Idea
Lenz's Law is a qualitative law that applies the law of conservation of energy to Faraday's Law, which states that any change in the magnetic field will cause an induced current. Lenz's law accounts for the direction of the new current - with the change coming from either the strength of the magnetic field, the direction of the magnetic field, the position of a circuit, the shape of a circuit, or the orientation of a circuit. In Lenz's words, "The current induced in a circuit due to a change in a magnetic field is directed to oppose the change in flux and to exert a mechanical force which opposes the motion." To keep the magnetic flux of a loop of wires constant, there is an induced magnetic field. Change in magnetic flux results in an equal and opposite change in the loop which is why we use negative [math]\displaystyle{ {\frac{dB}{dt}} }[/math]. Below is a basic visualization of Lenz's Law where there is an existing magnetic field.
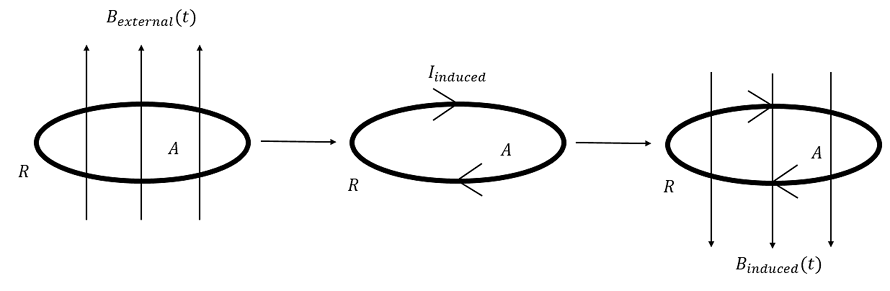 (image obtained from https://brilliant.org/wiki/lenzs-law/)
(image obtained from https://brilliant.org/wiki/lenzs-law/)
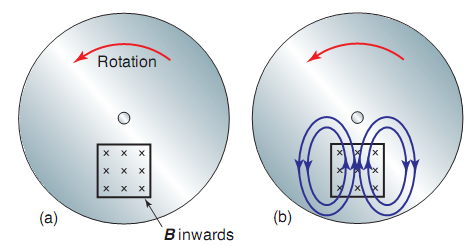
This Law is applied to determine the direction of current and the field it creates. When an induced field is generated by a change in magnetic flux (Faraday's Law), the induced current will flow creating its own magnetic field that opposes the magnetic field that created it. Direction is important when dealing with the law of conservation of energy. It can be seen applied when looking at electromagnetism such as the direction of voltage induced in an inductor.
In summary, whenever there is a change in magnetic flux in a conducting loop, the charge is balanced by the induction of a magnetic field. The integral of B * n remains constant.
Mathematical Model
Lenz's Law is mathematically modeled as part of Faraday's Law. The negative sign in the equation represents the opposing induced field. [math]\displaystyle{ \epsilon = -{\frac{d\phi}{dt}} }[/math] where [math]\displaystyle{ \epsilon }[/math] is the emf of the system and [math]\displaystyle{ d\phi }[/math] is the change in the magnetic field. This means the induced electromotive force and rate of change in magnetic flux both have opposite signs. While there is a formula, it is important to note that this is mainly a qualitative law and does not incorporate magnitude, only direction.
Example: The currents seen within strong magnets can create currents rotating in the opposite direction in metals like cooper or aluminum. If you were to drop a strong magnet through a cooper or aluminum pipe, you would observe that the velocity is decently slower than if you were to drop the magnet outside of the pipe as the induced current counters the change in flux. The same thing occurs for magnets being passed through a coil. A visualization of this is shown below:
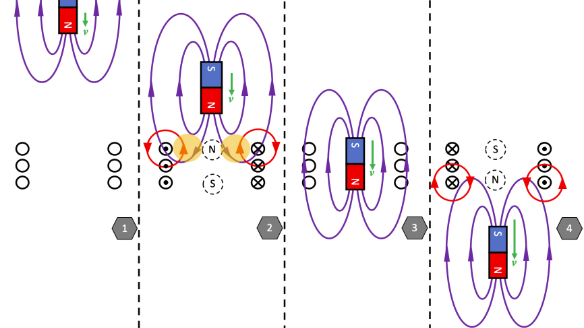 (image obtained from https://physicsteacher.blog/2021/04/18/nature-abhors-a-change-in-flux/)
(image obtained from https://physicsteacher.blog/2021/04/18/nature-abhors-a-change-in-flux/)
Picture 1: The magnet is far from the coil and moving slowly. At this distance, it produces no magnetic flux through the center of the coil. Since there's no change in magnetic flux, Faraday’s Law tells us there is no induced current.
Picture 2: As the magnet falls, it accelerates and approaches the coil, now generating magnetic flux within it. The increasing flux induces a current, as per Faraday’s Law. Using Lenz’s Law, the induced current creates a magnetic field that opposes the magnet's increasing flux. This essentially forms a temporary north pole at the top of the coil, repelling the falling magnet. This magnetic repulsion reduces the magnet’s acceleration (it falls at less than g).
Picture 3: While the magnet is centered in the coil, the magnetic flux through the coil remains roughly constant. Since there's no change in flux, no current is induced and no opposing force is generated. The magnet accelerates downward at g.
Picture 4: As the magnet leaves the coil, the magnetic flux through the coil decreases, triggering an induced current. According to Lenz’s Law, this current flows in a direction that tries to maintain the original flux—creating a north pole at the bottom of the coil, again opposing the magnet’s motion. This produces an upward magnetic force that slows the fall (again, acceleration is less than g).
Computational Model
Explore Lenz’s Law interactively with the PhET simulation linked below:
This simulation demonstrates electromagnetic induction using a movable bar magnet, a coil of wire, and measurement tools such as voltmeters and field indicators. Users can observe how changes in magnetic flux generate an induced emf, and how the direction of the induced current follows Lenz’s Law. The simulation also allows adjustment of magnet strength, coil turns, and speed, giving a clear visual explanation of flux, induction, and opposition fields.
Right Hand Rule
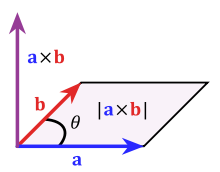
The Right Hand Rule is a heuristic used to determine the direction of angular momentum as a vector. The direction of angular momentum is determined by calculating the cross product of the vectors. To use the Right Hand Rule, place your thumb in the direction of [math]\displaystyle{ -dB }[/math] and curl your fingers. The direction of the non-coulombic electric field is the same direction as your fingers curl. An example of how the cross product is performed is below.
Right Hand Rule for Lenz's Law
To determine the direction of the induced current in a loop, the right-hand rule is applied after identifying the direction of the induced magnetic field. Since Lenz’s Law states that the induced current will create a magnetic field that opposes the change in magnetic flux, the first step is to decide whether the external flux is increasing or decreasing, and whether it points into or out of the page. Once the direction of the induced magnetic field is known, the right-hand rule gives the corresponding direction of current.
Point your thumb in the direction of the induced magnetic field (the direction required to oppose the change in flux). The curl of your fingers shows the direction of the induced current around the loop. A thumb pointing *out of the page* corresponds to a counterclockwise current, while a thumb pointing *into the page* corresponds to a clockwise current.
This procedure works because a current in a closed loop always produces a magnetic field following the right-hand rule. Lenz’s Law determines which direction that magnetic field must point; the right-hand rule then determines how the charges must circulate to produce it.
Examples
Right Hand Rule
In the examples above, the direction of the electric field is the pink arrows. This can be determined by first placing your thumb in the direction of the [math]\displaystyle{ -dB }[/math] and then curling your fingers. The direction your fingers curl is the direction of the electric field.
Example 1: Easy
A solenoid has current [math]\displaystyle{ I_1 }[/math] flowing around it increasing from 0 to 40A. A plain loop of wire is placed around the solenoid, perpendicular to the axis of the solenoid. An emf is produced, therefore producing an [math]\displaystyle{ I_2 }[/math]. Are [math]\displaystyle{ I_1 }[/math] and [math]\displaystyle{ I_2 }[/math] flowing in the same direction or opposite?
Solution
The original current [math]\displaystyle{ I_1 }[/math] produced a magnetic field. In order to maintain the conservation of energy and Newton's Third Law, the magnetic field produced by [math]\displaystyle{ I_2 }[/math] must oppose this field. This is in accordance with Lenz's Law. Therefore, [math]\displaystyle{ I_2 }[/math] must oppose [math]\displaystyle{ I_1 }[/math] in direction.
Example 2: Medium
An magnet is moving through a copper tube (velocity drawn). Find the direction of -dB/dt and the direction of the induced current. Remember to use the right hand rule.
Draw/write the direction of [math]\displaystyle{ -{\frac{dB}{dt}} }[/math], as well as the induced current for each of these scenarios (as viewed from above). Note: remember the magnetic field for a dipole!
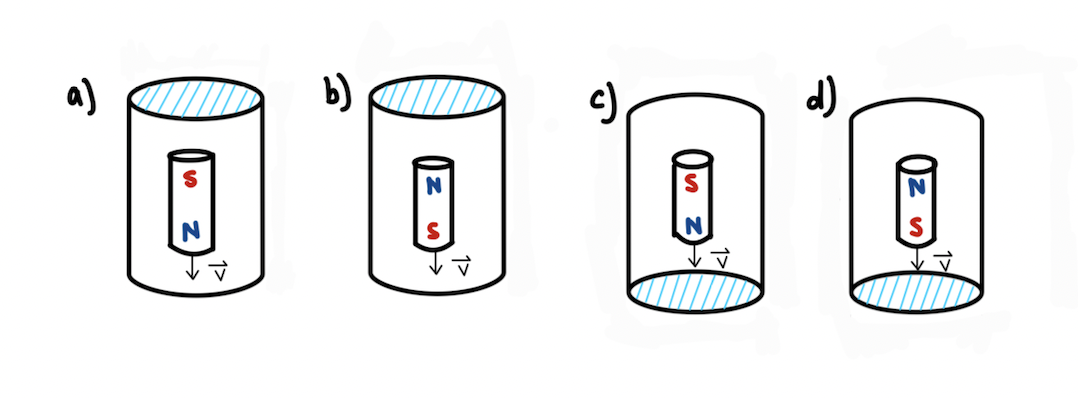 Graphic created by Nicole Romer, Digitalized by Lucia Jang
Graphic created by Nicole Romer, Digitalized by Lucia Jang
Use [math]\displaystyle{ B_i }[/math] and [math]\displaystyle{ B_f }[/math] to find [math]\displaystyle{ -{\frac{dB}{dt}} }[/math] & use the RHR to determine the direction of the current. Note:[math]\displaystyle{ -{\frac{dB}{dt}} }[/math] is equal to [math]\displaystyle{ B_i - B_f }[/math]
Solution A)-y, clockwise B)+y, counterclockwise C)+y, counterclockwise D)-y, clockwise File:LenzLawSolutionA.png
The magnetic field in this graphic is decreasing at a rate of 5.0mT/s. What is the direction of the current in the circle of wire?
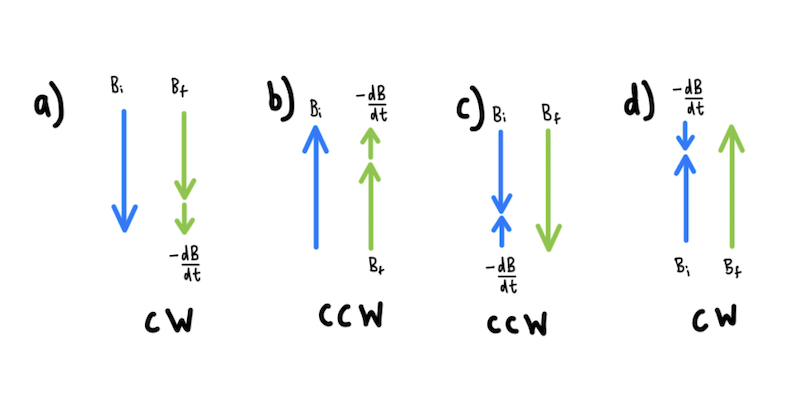 Graphic created by Nicole Romer, Digitalized by Lucia Jang
Graphic created by Nicole Romer, Digitalized by Lucia Jang
Solution The current in the circle of wire will produce a magnetic field that needs to supplement the existing diminishing field. This is in accordance with Lenz's Law. Therefore, the magnetic field produced needs to be into the page. Using the right hand rule, to produce a field going into the page the current in the circle of the wire must be in the clockwise direction.
Example 3: Difficult
The magnetic field is decreasing at a rate of 5.0mT/s. The radius of the loop of wire is 5.0m, and the resistance is 5 ohms. What is the magnitude and direction of the current?
Solution
To find the magnitude of the current we must first use the formula [math]\displaystyle{ \epsilon = -{\frac{d\phi}{dt}} }[/math] to find the [math]\displaystyle{ \epsilon }[/math] representing the emf of the system. We know, more specifically, that [math]\displaystyle{ \epsilon = -NAcos\theta{\frac{d\phi}{dt}} }[/math]. Therefore, [math]\displaystyle{ \epsilon = -1*5.0^2*\pi*1*-5*10^{-3} }[/math] which resolves to [math]\displaystyle{ \epsilon = .392699 }[/math]. From there, to find the current we know that [math]\displaystyle{ I = {\frac{\epsilon}{R}} }[/math]. Plugging in the values we know we find, [math]\displaystyle{ I = {\frac{.392699}{5.0}} = .07854A }[/math]. That is the magnitude of the current. To find the direction we must use Lenz's Law. The current in the circle of wire will produce a magnetic field that needs to supplement the existing diminishing field. Therefore, the magnetic field produced needs to be into the page. Using the right hand rule, to produce a field going into the page the current in the circle of the wire must be in the clockwise direction.
Common or Recent Explanations
Just as Aristotle once said "Nature abhors a vacuum," American physicist David J. Griffiths justified Lenz's law in the simple idea that "nature abhors a change in flux." Therefore, when a change in magnetic flux is experienced, an induced current is formed that counters this change, ideally leading to no net change in flux, but often just working to reduce the rate of change in the flux rather than completely nullifying it. This is why there is a negative sign in the equation [math]\displaystyle{ {\frac{dB}{dt}} }[/math]
Connectedness
An application of Lenz's Law is to cause rotation to create energy. In industry, Lenz's Law can be applied to electric generators or motors. When a current is induced in a generator, the direction of the induced current will flow in opposition of the magnetic field that created it. This causes rotation in the generator.
Another application of Lenz's Law is in electromagnetic braking for vehicles. This process begins with electromagnets inducing eddy currents into the spinning rotor. Magnetic fields that oppose the initial change in magnetic flux are created from these eddy currents. This slows the rotor.
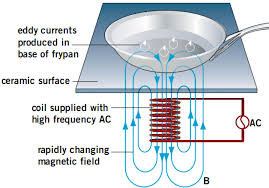
One last application of Lenz's Law is induction stove tops. These cooktops heat up as a result of changing magnetic fields and eddy currents operating according to Lenz's Law.
History
Henrich Friefrich Emil Lenz (1804-1865), a Russian physicist of German origin was born in Dorpat, nowadays Tartu, Estonia. Henrich studied chemistry and physics at the University of Dorpat in 1820 after his secondary education. From 1823 to 1826, he traveled with the navigator, Otto von Kotzebue on his third expedition around the world. During this journey he studied climate conditions, and properties of seawater. After his travels, he worked at the University of St. Petersburg, Russia, where he later became the Dean of Mathematics and Physics from 1840 to 1863. In the year of 1831, he started studying electromagnetism, and soon after in 1835, what is known today as Lenz's Law was created. Lenz was also know for carefully checking his work, testing any variable that might effect his results. Lenz died on February 10, 1865, just two days before his 61st birthday, after suffering a stroke, while in Rome.
Further reading
Faraday's Law [1] Conservation Laws [2]
More Videos For Study
https://www.youtube.com/watch?v=xxZenoBs2Pg This links to a video by Khan Academy that explains how Lenz's Law works through an example.
https://www.youtube.com/watch?v=Vs3afgStVy4 This links to a video by Grand Illusions that displays Lenz's Law using a magnetic falling down a tube.
References
https://nationalmaglab.org/education/magnet-academy/history-of-electricity-magnetism/pioneers/heinrich-friedrich-emil-lenz http://hyperphysics.phy-astr.gsu.edu/hbase/conser.html http://regentsprep.org/regents/physics/phys08/clenslaw/ http://hyperphysics.phy-astr.gsu.edu/hbase/electric/farlaw.html http://farside.ph.utexas.edu/teaching/302l/lectures/node85.html http://www.electrical4u.com/lenz-law-of-electromagnetic-induction/