Length and Stiffness of an Interatomic Bond

Claimed by Fehmeen Tariq Fall 2019

This topic covers find the length and stiffness of an Interatomic Bond.

The Main Idea

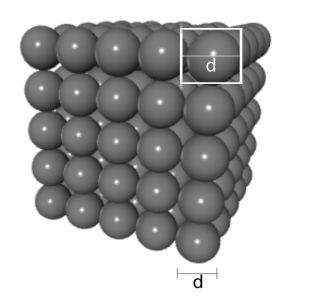
A solid object is made up of a large amount of atoms that are held together by chemical bonds in a lattice-like structure as seen in Figure 1. Each atom is connected to its neighboring atoms by these chemical bonds. One way to approximate this solid object model is to imagine the atoms as balls and the chemical bonds as springs-- a ball and spring model! The relaxed length of the microscopic spring between two atoms is just the distance from the center of one atom to the center of the other atom, [math]\displaystyle{ d }[/math]. For our object, the distance is just twice the radius of one of the atoms since the electron cloud of the atom fills in the extra space. If the atoms are in a cubic arrangement that means that the volume of each atom would be [math]\displaystyle{ d × d × d }[/math] and would have a cross-sectional area of [math]\displaystyle{ d × d }[/math].

Figure 1

Since the interatomic bonds are modeled as springs, they have a stiffness, [math]\displaystyle{ k_{si} }[/math], that relates the interatomic force to the stretch of the interatomic bonds. We use [math]\displaystyle{ s }[/math] for the microscopic stretch.

With this information, we can determine the stiffness of an interatomic bond. In order to determine stiffness, we must determine the length of an interatomic bond in a particular material. For different materials, bond lengths will vary slightly depending on the size of the atoms. The length of one interatomic bond is defined as the center-to-center distance between two adjacent atoms, which is just the distance of the two atoms' radii added together since we use the space-filling model. To find the radius, we divide the diameter of a single atom in half. So, the center-to-center distance is essentially equal to the diameter of a single atom since in the space-filling model there is no space between each atom. If we can calculate the length of the interatomic bond (the diameter of a single atom), we can use this data to find the stiffness of the interatomic bond, modeled as a spring.

Length of an Interatomic Bond

The length of an interatomic bond is defined as the center-to-center distance between adjacent atoms. This is the same as the diameter of an atom (including the full electron cloud).

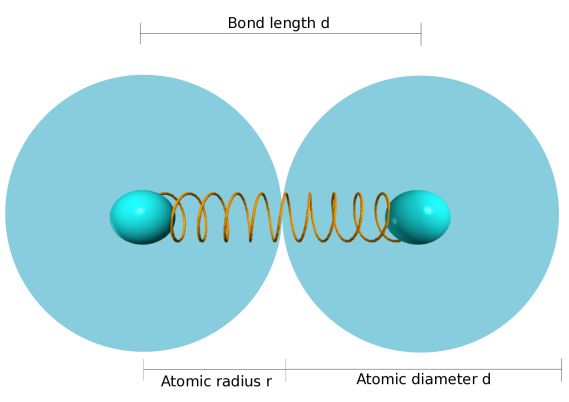
We can calculate atomic diameters for crystals of particular elements by using the measured density of the material in kilograms per cubic meter and Avogadro's number (the number of atoms in one mole of the material), 6.02 X 10^23 atoms per 1 mol.

The mass of one atom can be determined using the mass of one mole and dividing it by [math]\displaystyle{ 6.022 x 10^{23} }[/math] atoms (Avogadro's number)

The Stiffness of an Interatomic Bond

It is difficult to measure the stiffness of an interatomic bond directly, so instead we can analyze data from macroscopic experiments to determine this quantity. We will consider the stiffness of an interatomic bond as a spring.

The equation for stiffness is: [math]\displaystyle{ |F| = k_{si}|s| }[/math]

Springs in Series

Springs in series refers to when springs are linked end-to-end.

Two identical springs linked end to end stretch twice as much as one spring when the same force is applied. The combined spring therefore is only half as stiff as the individual springs.

Springs in Parallel

Springs in parallel is when springs are linked side-by-side.

We can think of the two springs as a single, wider spring. Two springs side by side are effectively twice as stuff as a single spring.

Cross-Sectional Area

The cross-sectional area of an object is the area of a flat surface made by slicing through the object.

For example, the cross-sectional area of a cylinder is the area of a cicle and the cross-sectional area of a rectangular solid is the area of a rectangle.

Mathematical Model

Formulas to Know

In many problems, you will be given the density of the solid that you are being questioned on. It is important to remember that [math]\displaystyle{ {density} = \frac{mass}{volume} }[/math] Number of bonds in one "chain" of the solid: [math]\displaystyle{ n_{bonds}={\frac{L}{d_{atomic}}} }[/math]

Spring Constant for one chain in the overall material: [math]\displaystyle{ k_{chain}({\frac{k_{atomic}}{n_{bonds}}}) }[/math]

Number of "chains" in the solid: [math]\displaystyle{ n_{chains}={\frac{A_{wire}}{A_{atom}}}={\frac{A_{wire}}{{(d_{atomic})}^2}} }[/math]

Spring constant for the overall material: [math]\displaystyle{ k_{wire}=k_{chain}×n_{chains} = k_{atomic} ({\frac{n_{chains}}{n_{bonds}}}) }[/math] [math]\displaystyle{ k_{wire}=k_{atomic}( {\frac{A_{wire}}{L_{wire}}})({\frac{1}{d_{atomic}}}) }[/math]

Examples

Example 1

The US Penny is actually made of zinc. A typical penny has a diameter of 1.905 cm and an average thickness fo 1.228 mm. The density of zinc is 7140 kg/m^3 and its atomic weight is 65.4 amu = 65.4 g/mol. Young's modulus of zinc is 1.022 e11 N/m^2.

a. Determine the mass of a typical penny.

[math]\displaystyle{ ρ = {\frac{m}{v}} }[/math]

[math]\displaystyle{ m = ρ v = ρ(hπr^2) = ρ(hπ({\frac{d}{2}})^2) }[/math]

[math]\displaystyle{ m = (7140)(1.228e-3)(π)({\frac{1.905e-2}{2}}^2) }[/math]

[math]\displaystyle{ m = 0.002499\ kg = 2.499\ g }[/math]

b. What is the diameter of a single zinc atom?

[math]\displaystyle{ n_{atoms} = (2.499\ g)({\frac{1\ mol}{65.4\ g}})({\frac{6.022e23\ atoms}{1\ mol}})=2.3e22\ atoms }[/math] [math]\displaystyle{ m_{atom} = {\frac{0.002499\ kg}{2.3e22\ atoms}} = 1.09e-25\ kg*m^3 }[/math]

[math]\displaystyle{ ρ = {\frac{m_{atom}}{v_{atom}}} }[/math]

[math]\displaystyle{ v_{atom} = {\frac{m_{atom}}{ρ_{atom}}} = {\frac{1.09e-25\ kg*m^3}{7140\ kg}}=1.53e-29\ m^3 }[/math]

[math]\displaystyle{ v_{atom} = (d_{atom})^3 }[/math]

[math]\displaystyle{ d_{atom} = (v_{atom})^{1/3}=(1.53e-29\ m^3)^{1/3} = 2.48e-10\ m }[/math]

c. How many zinc atoms make up one side of the penny?

[math]\displaystyle{ {\frac{area\ of\ penny\ face}{cross-sectional\ area\ of\ one\ atom}}={\frac{π({\frac{d}{2}})^2}{π({\frac{d_{atom}}{2}})^2}}={\frac{(1.095e-2)^2}{(2.48e-10)^2}} = 1.95e15\ atoms }[/math]

d. Calculate the interatomic spring stiffness for zinc.

[math]\displaystyle{ y = {\frac{k_{si}}{d_{atom}}} }[/math]

[math]\displaystyle{ k_{si} = y*d_{atom} = (1.077e11)(2.48e-10) = 26.7096\ {\frac{N}{m}} }[/math]

Example 2

A copper wire is 2m long. The wire has a square cross section. Each side of the wire is 1mm in width. Making sure the wire is straight, you hang a 10 kg mass on the end of the wire. The wrie is now 1.67 mm longer. Determine the stiffness of one interatomic bond in copper.

Step 1 Spring Stiffness of Entire Wire

[math]\displaystyle{ Δp_y = 0 = (k_{s,\ wire}*s-mg)Δt }[/math]

[math]\displaystyle{ k_{s, wire} = {\frac{mg}{s}} = {\frac{(10\ kg)(9.8\ N/kg)}{(1.67e-3\ m)}}= 5.87e4\ N/m }[/math]

Step 2 Cross-Sectional Area of Wire

[math]\displaystyle{ A_{wire} = (1e-3\ m)^2 = 1.6e-6\ m^2 }[/math]

Step 3 Cross-Sectional Area of One Atom

[math]\displaystyle{ A_{atom} = (2.28e-10\ m)^2 = 5.20e-20\ m^2 }[/math]

Step 4 Number of Chains

[math]\displaystyle{ n_{chains} = {\frac{A_{wire}}{A_{atom}}} = {\frac{1e-6\ m^2}{5.2e-20\ m^2}} = 1.92e13 }[/math]

Step 5 Number of Bonds in One Chain

[math]\displaystyle{ n_{bonds} = {\frac{L_{wire}}{d}} = {\frac{2\ m}{2.28e-10\ m}} = 8.77e9 }[/math]

Step 6 Stiffness of One Interatomic Spring

[math]\displaystyle{ k_{s, wire} = {\frac{(k_{si})(n_{chains})}{n_{bonds}}} }[/math]

[math]\displaystyle{ k_{si} = {\frac{(k_{s,wire})(n_{bonds})}{n_{chains}}}={\frac{(5.87e4)(8.77e9)}{1.92e13}} = 26.8\ N/m }[/math]

Example 3

If a chain of 50 identical short springs linked end to end has a stiffness of 270 N/m, what is the stiffness of one short spring?

[math]\displaystyle{ Total\ number\ of\ springs\ = n = 50 }[/math]

[math]\displaystyle{ Effective\ stiffness\ constant\ = k_{eff} = 270\ N/m }[/math]

[math]\displaystyle{ Stiffness\ constant\ of\ each\ spring\ = k_{s} }[/math]

[math]\displaystyle{ {\frac{1}{k_{eff}}}={\frac{n}{k_{s}}} }[/math]

[math]\displaystyle{ k_{s}=n*k_{eff} }[/math]

[math]\displaystyle{ k_{s} = 50 * 270\ N/m }[/math]

[math]\displaystyle{ k_{s} = 13500\ N/m }[/math]

Example 4

Forty-five identical springs are placed side by side and connected in parallel to a large massive block. The stiffness of the 45-spring combination is 20,250 N/m. What is the stiffness of one of the individual springs?

[math]\displaystyle{ Total\ number\ of\ springs\ = n = 45 }[/math]

[math]\displaystyle{ Effective\ stiffness\ constant\ = k_{eff} = 20250\ N/m }[/math]

[math]\displaystyle{ Stiffness\ constant\ of\ each\ spring\ = k_{s} }[/math]

[math]\displaystyle{ k_{eff}=n*k_{s} }[/math]

[math]\displaystyle{ k_{s} = {\frac{k_{eff}}{n}} }[/math]

[math]\displaystyle{ k_{s} = {\frac{20250\ N/m}{45}} }[/math]

[math]\displaystyle{ k_{s} = 450\ N/m }[/math]

Example 5

Five identical springs, each with stiffness 390 N/m, are attached in parallel (that is side by side) to hold up a heavy weight. If these springs were replaced by an equivalent single spring, what should be the stiffness of this single spring?

[math]\displaystyle{ k_{eff}=n*k_{s} }[/math]

[math]\displaystyle{ k_{s}=390\ N/m }[/math]

[math]\displaystyle{ n = 5 }[/math]

[math]\displaystyle{ k_{eff} = {5}*{390\ N/m} }[/math]

[math]\displaystyle{ k_{eff} = {1950\ N/m} }[/math]

Connectedness

How is this topic connected to something that you are interested in?

Materials are all made up of atoms and their connections. Its interesting to see how we can apply macroscopic observations to a microscopic topic.

How is it connected to your major?

Biomedical Engineers must always chose the right materials when creating devices for humans. Depending on their use, a material might not need to be very durable, or it may need to be the opposite, and be extremely durable.

Is there an interesting industrial application?

Bonds are found in every material and object, so how these different bonds are connected create different objects and its really cool.

References

Matter and Interactions By Ruth W. Chabay, Bruce A. Sherwood - Chapter 4

http://www.webassign.net/question_assets/ncsucalcphysmechl3/lab_10_1/manual.html

Created by Emily Milburn