Introduction to Magnetic Force

This page provides a short introduction to the concept of the magnetic force.

Main Idea

The magnetic force acts upon moving charges (or currents). This means that the magnitude of the magnetic force has a direct dependence on the velocity of the charge it is acting upon. Furthermore, the magnetic force acts via the magnetic field. This magnetic force acts in a direction perpendicular to both the velocity of the charge and the direction of the magnetic field.

The magnetic field is a vector field (meaning that it extends in all three dimensions). Magnetic fields are provided most simply either by moving charges or by dipoles. When the magnetic field strength is known, it makes finding the magnetic force quite simple.

Magnetic fields and electric fields are, in fact, related, and both together comprise the electromagnetic force. This force is the second strongest of the four fundamental forces, behind the nuclear strong force, and ahead of the weak force and the gravitational force.

A Mathematical Model

Magnetic force can be represented as follows, where q is the charge on a particle, v is that particles velocity, and B is the magnetic field. Here, [math]\displaystyle{ \theta }[/math] represents the angle between the velocity and magnetic field vectors. The direction of the magnetic field can be found using the right hand rule.

[math]\displaystyle{ \vec{\mathbf{F_B}}=q\vec{\mathbf{v}}\times{}\vec{\mathbf{B}} }[/math]
[math]\displaystyle{ |\vec{\mathbf{F_B}}|=qvBsin(\theta{}) }[/math]

The above means that any particle at rest will NOT experience any magnetic force.

The magnetic force also applies to a current carrying wire. Because a current is essentially made of moving charges, this means that the current carrying wire will experience a force. This force is directly proportional to the length of the wire and the current in that wire, as is displayed below. Here I is the magnitude of the current, which is in units amperes, or Coulombs/second, l is in units of length, and is in the same direction as the current (for the cross product).

[math]\displaystyle{ \vec{\mathbf{F_B}}=I\vec{\mathbf{l}}\times{}\vec{\mathbf{B}} }[/math]
[math]\displaystyle{ |\vec{\mathbf{F_B}}|=IlBsin(\theta{}) }[/math]

Examples

Simple

Say you have a 1 C charge moving at a rate of 3 m/s. This velocity makes an angle of 60 degrees with respect to a magnetic field with strength 2 Tesla. What is the magnitude of the force the charge experiences?

The units given in the problem statement are all proper SI units, and so the numbers can just be plugged in to the following equation:

[math]\displaystyle{ F_B=qvBsin(\theta{}) }[/math]

[math]\displaystyle{ F_B=(1 C)(3 m/s)(2 T)(sin(60))=5.196 N }[/math]

Thus the answer to this problem is, straightforwardly, 5.196 N.

Middling

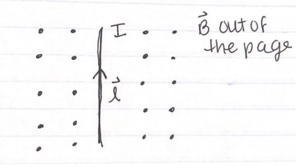
Suppose you have a wire with a current [math]\displaystyle{ I=6 }[/math] amps. This wire is sitting in a constant magnetic field of magnitude 1 T. This wire has length 6 cm. What is the magnitude and the direction of the force acting upon the wire? The magnetic field is pointing out of the page (reference the diagram at right).

The easiest first step would be to determine the direction of the magnetic force. By using the right hand rule, we can determine that when the current length, which is going up, is crossed with a vector pointing out of the page, the resulting vector would point towards the right, in the so-called positive x-direction.

Next, we can determine the magnitude of the resultant force via the following relation. Because [math]\displaystyle{ \theta{} }[/math] here is equal to 90 degrees, [math]\displaystyle{ sin(\theta{}) }[/math] is equal simply to one.

[math]\displaystyle{ F_B=IlBsin(\theta{}) }[/math]
[math]\displaystyle{ F_B=(6A)(0.06m)(1T)=0.36N }[/math]

Finally, as stated before, we know that this is solely in the positive x-direction due to the right hand rule.

Hard

See this problem under the Magnetic Force section on the Physics 2 page

Connectedness

The magnetic force contributes heavily to specific phenomenon in astrophysics. Specifically, neutron stars have large magnetic fields, causing electrons to be accelerated and emit a type of radiation known as synchrotron radiation. Indeed, there are certain types of neutron stars known as magnetars that have unusually high magnetic field strengths that then power the emission of X-rays and gamma rays (the highest energy type of electromagnetic radiation). Furthermore, there are also strong magnetic fields around black holes.

As a physics major, understanding how magnetic fields affect the motion of particles and their behavior is fundamental.

The magnetic force is connected directly to MRI's (magnetic resonance imaging). Using MRI's, doctors can learn a great deal about the current condition of the human body, including tracking cancerous tumors and diagnosing different injuries and diseases.

History

Initially, electricity and magnetism were thought to be separate forces. When Maxwell published his A Treatise on Electricity and Magnetism, however, it was realized that the two forces were interrelated. Later, in 1820, a Danish physicist realized that the magnetic field from a circuit could be turned on and off if the circuit was turned on and off. This was when it was realized that magnetic fields radiate from all sides of a wire carrying an electric current, providing proof that electricity and magnetism were definitely interrelated.

These findings kickstarted a period of intensive research into attempting to find a mathematical representation of the relationship between electricity and magnetism, and the result would be one of the defining accomplishments of the 19th century in physics.