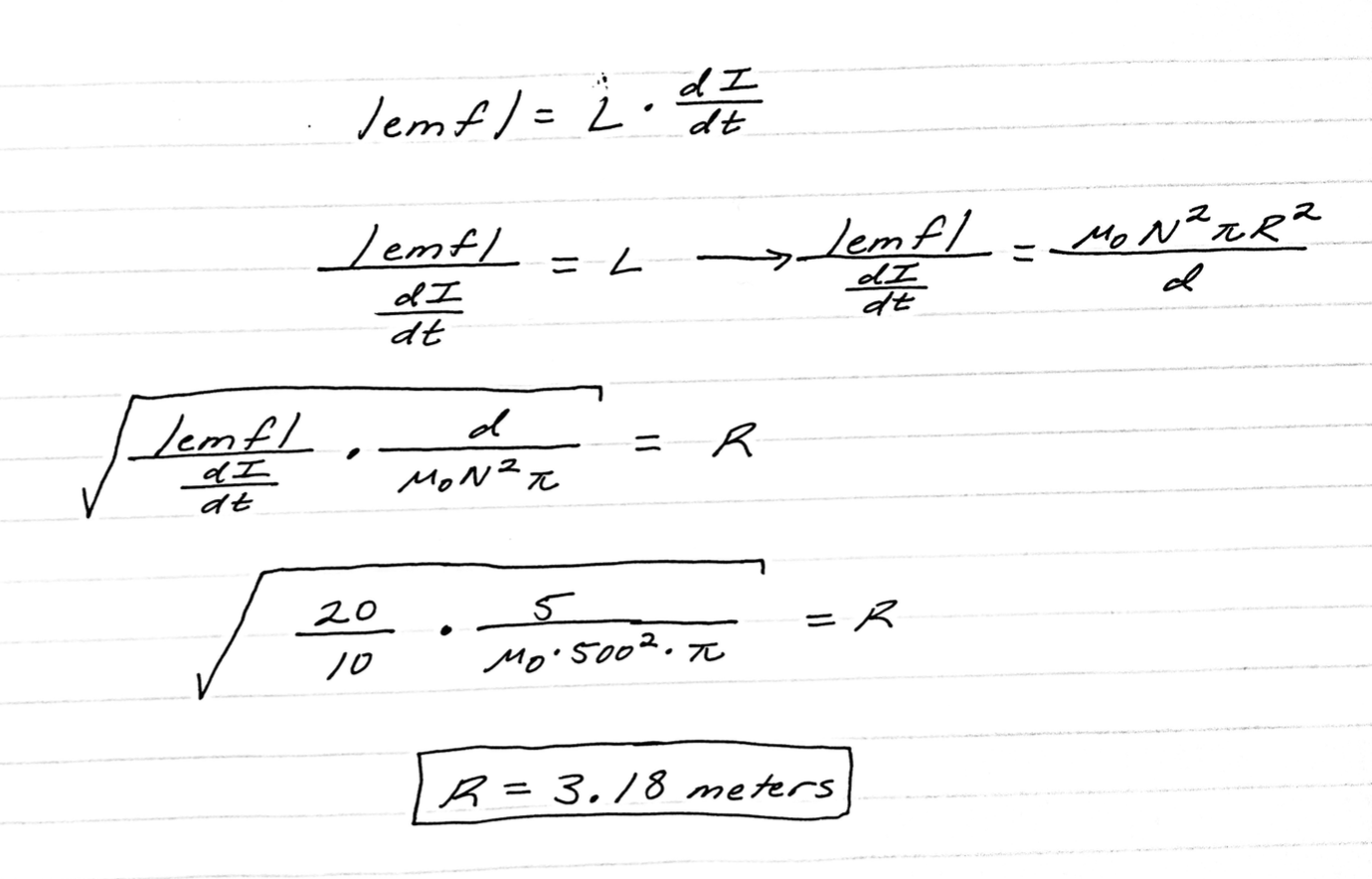Inductors
Short Description of Inductors Rohan Mundkur (Fall 2016)
Inductors - Conceptual Overview
An inductor's broad purpose, within circuits, is to resist changes in current. Upon examining the structure and characteristics of inductors, we are able to develop mathematical and conceptual arguments that explain this behavior. Inductors typically consist of a conductor, usually wire, wrapped in a coil.
The conductor that makes up the inductor will have a current running through it, and as this non-changing current runs, a magnetic field will be created within the center of the coil. Therefore, as the current begins to change, the respective flux through a ring of the coil will change as well. As we know, the ratio of a change in flux to the respective change in time will provide us with the potential difference resulting from the change in current. By multiplying this potential difference by the number of loops in the circuit, we are able to obtain the coil's overall potential difference due to the single change in current.
The essential directional behavior of the induced emf is to be opposite the coil's magnetic field when the current increases and in line with the coil's magnetic field when the current decreases. We can make this assumption because if the behaviors were reversed, any change in current would result in an infinite increase or decrease. This phenomenon occurs because of the direction of the non-Coulomb (NC) electric field's direction in relation to the Coulomb electric field's direction (direction of current). When the current through the inductor increases, the NC electric field curls in the opposite direction of the current, but when the current through the inductor decreases, the NC electric field curls in the same direction as the current.
The mathematical characterization of this phenomenon will be described in greater detail below.
Mathematical Model and Explanation
As we established earlier, an inductor's emf has roots in ratio of change in flux to change in time. We most often look at solenoids when discussing inductors, so the explanations and diagrams below will be solenoid specific though the concepts can be applied to coils with any shape - this is the case as flux is dependent on area.
The derivation below begins by providing the formula for the magnetic field within a solenoid and continues by applying this magnetic field (and subsequent changes due to change in current) to the equation for flux given the solenoid is comprised of "N" rings with radius "R". After determining the emf of a single loop, we multiply by "N" to obtain the emf of the entire solenoid. Finally, in order to simplify our expression and provide a segway to the exploration of non-solenoid inductor shapes, we represent the proportion of total emf to change in current by the variable "L" whose units are henries (H).
Computational Model
The following sequence is a visualization of inductors in a simple circuit
Note, inductance and resistance have inverse effects on current.
Here's one final gif to show how inductors are crucial in the design of power supplies. See how the force is created?
(original simulation created by Eugene Khutoryansky on Youtube)
Examples
Simple
What is the magnitude of the induced emf of one loop of a 300 turn solenoid that has a radius of 5 cm and length of 2 m when the current running through the solenoid decreases by 1 Amp/second?
We must first realize that this question only requests that we provide the emf of a single loop. Therefore, we must ensure that we only use a single "N" term rather than "N^2". Once we simplify our overall emf equation so that it applies to a single loop, we can plug in our values and solve from there.
Middling
A 5 meter solenoid with 500 turns of copper wire creates an emf with a magnitude of 20V when current increases by 10 Amps/second. What is the radius of the coil?
We begin with our simplified expression and begin algebraic rearrangements to create an expression that provides us with a value for "R". After this, we simply plug in the values we are given, and compute our radius.
Difficult
An infinite straight wire with current I is next to a solenoid of 10 square loops with dimensions L. The side of the solenoid closest to the wire is at a distance "s".
Connectedness
How is this topic connected to something that you are interested in?
I find the concept of inductance incredibly interesting because it serves as an almost natural buffer to any deviation from "equilibrium". This intrigues me because I find biology and chemistry very interesting, and within those two subjects, we often discuss homeostasis and chemical equilibrium and the natural buffers that exist in order to counteract movements away from the state of equilibrium.
Is there an interesting industrial application?
Inductors have a vast range of industrial applications ranging from transformers that help manage the power supply to massive cities or energy storage for personal computers. The defining characteristics of inductors also enable them to be used at traffic lights in order to gauge traffic flow at intersections. Living in Atlanta, we all know the horrors of rush hour, so I find this industrial application incredibly interesting.
For more information on how inductors play a role in traffic control, please visit this link from HowStuffWorks: http://auto.howstuffworks.com/car-driving-safety/safety-regulatory-devices/question234.htm
How is it connected to your major?
The concept of inductors does not directly relate to my major as I am a Business major. However, I am taking Pre-Medical Courses, and as mentioned earlier in this section, the way in which inductors provide a natural buffer within circuits is mirrored through various biology and chemistry concepts.
History
Joseph Henry is the father of inductance. Although Joseph Henry's work on self-inductance may not hold the same place in common knowledge as Sir Isaac Newton's Laws, Henry had an enormous impact on history during the 19th century. The American scientist discovered self-inductance when performing experiments with electromagnets, and although much credit for this work is given to the Englishman Michael Faraday, who published his work first, many suggest that Henry discovered these concepts first. Because of Henry's importance in this field, the units of inductance take his name: henry (H).
Henry also greatly impacted scientific advancement within America as he was the first Smithsonian Secretary.
The discovery of inductors quickly led to the discovery of something super cool: transformers. The simplest version of a transformer is just two inductors next to each other not touching because the magnetic field of each inductor affects the other. This discovery kicked off years of experimentation. Eventually, William Stanley of George Westinghouse created the first commercially viable transformer in the 1880s. This launched George Westinghouse into the public consciousness and they quickly became a worldwide infrastructure powerhouse--even powering the World’s Columbian Exposition in Chicago in 1893.
In a greater, historical perspective, the introduction of inductors into complex circuits provided the basis for the evolution of modern power grids and electric technology as we know it today. The supply of the massive amounts of electricity that today's society consumes would be incredibly unstable without transformers, whose properties are made possible by inductors.
See also
Further reading
https://www.lifewire.com/applications-of-inductors-818816
http://electronics.howstuffworks.com/inductor3.htm
http://auto.howstuffworks.com/car-driving-safety/safety-regulatory-devices/question234.htm
https://www.aps.org/programs/outreach/history/historicsites/henry.cfm
References
Matter & Interactions, Volume 2 4th Edition (Section 22.6)
https://www.quora.com/What-is-the-function-of-inductors-and-capacitors
http://electronics.howstuffworks.com/inductor.htm
http://www.edisontechcenter.org/JosephHenry.html