Gravitational Force in Space and Other Applications
This page looks into the gravitational force in space, and other applications of the gravitational force. Kepler's Laws are also explained here.
Main Idea
The gravitational force, as it acts in space, can be used to explain the motions of celestial bodies, and thus is of extreme interest when predicting future events in our Solar System.
Johannes Kepler, prior to Newton, had created laws to explain the motion of celestial bodies. His laws, explained below, were further proven by Newton's idea of gravity, which can explain why these laws are true.

- Kepler's first law states that all planets move about the Sun in an elliptical orbit, with the Sun at one of the foci of the ellipse. This can be further elaborated to say that every body orbits around the center of mass in its system on an elliptical orbit. For example, in the Earth-Moon system, the Moon orbits around the Earth in an elliptical orbit, with the Earth at one of the foci of the ellipse. An ellipse, in this case, can be a circle, oval, parabola, or hyperbola, depending on the type of motion of the orbiting body. The gravity of the Sun keeps the object bound on the orbit, with the force of gravity always pointing radially inwards towards the Sun. This constantly changing direction of gravitational force is what keeps the planet bound.
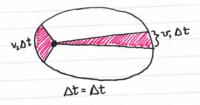
- Kepler's second law, the law of equal areas, states that a planetary body sweeps out an equal area in its orbit in equal time. This is also shown in a diagram. Basically, if you draw a line from the planet to the Sun, the area that is created in some time segment by the motion of the planet will be the same as the area created in an equivalent time segment at a different point in the objects orbit. This can also be explained by the gravitational force, and the conservation of angular momentum, which will be covered later in the course.
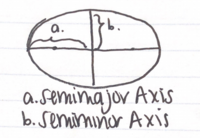
- Kepler's third law states that the square of the orbital period of the planet (the time it takes to go around the Sun) is directly proportional to the cube of its semi-major axis (which is half of the length of the longer axis of the ellipse, and is shown in a diagram). This law is incredibly useful, especially in determining the semi-major axis of exoplanets when we know their period from transits (it can be detected when the planet passes in front of the star. By measuring the timing of these transits, the period of the planet can be determined).
Newton's law of gravitation also functions in space much the same as it does almost everywhere else classically, and expressions of this force can be used to determine whether or not planets or other celestial bodies are bound to a star, or if they are just floating through space.
A Mathematical Model
The easiest of Kepler's three laws to formulate mathematically is Kepler's 3rd Law. By setting the net force equal to the gravitational force, we can derive a simple equation for the period of the planet.
- [math]\displaystyle{ F_{net}=ma=\frac{Gm_{1}m_{2}}{r^{2}} }[/math]
In a circular orbit, the acceleration of planet is equal to the square of its velocity over the radius of the orbit. This will be further explained later, when the centripetal force is covered, but for this purpose, we can accept this relationship and replace ma in our equation.
- [math]\displaystyle{ F_{net}=\frac{mv^2}{r}= \frac{Gm_{1}m_{2}}{r^{2}} }[/math]
Through simple manipulation of this net force, we can determine that the period (which is equal to [math]\displaystyle{ \frac{2{\pi}r}{v} }[/math]) squared is proportional to the radius cubed. While this is just a simple derivation for a circular orbit, the same holds true for elliptical orbits, and, in fact, when you use years for the units of period, and astronomical units (1 AU = the distance from the Earth to the Sun) for the semi-major axis (a), the following equation holds true for the solar system:
- [math]\displaystyle{ P^2=a^3 }[/math]
A more rigorous approach (with mass in solar masses, and [math]\displaystyle{ M_{total} }[/math] representing the total mass of the two bodies) provides the following equation:
- [math]\displaystyle{ (M_{total})P^2=a^3 }[/math]
Newton's Law of Gravity speaks on this force in a very refined way. It states that matter will experience some feeling if it is charged or not. Gravity depends on the two objects that are affected and the distance between them. So, it does not rely on the density or chemical structure of the matter involved. Matter with the same mass as the Sun will have an equal gravitational effect on the Earth as the Sun itself.
Larger amounts of mass create a higher amount of gravitational force. This relates to acceleration: heavier objects tend to produce better acceleration rates than lighter objects. Gravity’s relationship with distance is opposite: gravity decreases as the distance becomes larger. The confusion with this is that gravity never reaches zero because it has infinite range. Stars feel the gravity from different stars and galaxies feel gravity from other galaxies. The constantly appealing gravity can act over the biggest separations known to man.
Examples
Simple
If a planet is revolving around a star with the same mass as the Sun with a period of 2 years, what is the semimajor axis of that planet?
Recall, we know the formula to find the semi-major axis if period is known, as is shown below:
- [math]\displaystyle{ P^2 = a^3 }[/math]
Here, P = 2 years, which can then be replaced into the formula to find the final answer.
- [math]\displaystyle{ a^3 = 2^2 = 4 }[/math]
- [math]\displaystyle{ a = (4)^{1/3} = 1.587 AU }[/math]
Middling
Imagine a stellar binary. In this system, there is a 1.1 solar mass star and a 3 solar mass star orbiting each other with a period of 30 days. What is the semi-major axis of this orbit?
First, the period of this system must be converted from days to years.
- [math]\displaystyle{ years = days/365.25=30/365.25= 0.0821 years }[/math]
This value for years can then be put into the following equations:
- [math]\displaystyle{ (M_1+M_2)P^2=a^3 }[/math]
- [math]\displaystyle{ a=((M_1+M_2)P^2)^{1/3}=((1.1+3)(0.0821)^2))^{1/3} }[/math]
- [math]\displaystyle{ a=0.3023 AU }[/math]
Thus, the semimajor axis of the system is 0.3023 AU.
Hard
Please see this problem, listed generally under the gravitational force page.
Connectedness
Space has always fascinated me, starting from my time as a little kid. Looking up at the stars and wondering how they came to be and how they move has always been a part of my life. Knowing how gravity works at a massive level helps to further my understanding and quench my thirst for knowledge with regards to the stars.
I am a physics major, specifically concentrating in astrophysics, and thus this knowledge is extremely applicable to me. I do research in classical dynamics in space, and thus gravitational interactions are incredibly important to consider in my research. More broadly, however, the knowledge of how the planets move and their gravity can be used when conceptualizing how to send spacecraft in the most efficient way to other places in the solar system. Lots of launches make use of so-called gravity assist maneuvers in order to get to the planet or body in question in the quickest possible manner without utilizing too much fuel.
GPS devices also make use of the notion of relativity in order to locate their targets. Without considering general relativity (which takes into account gravity in space), GPS devices would not function as planned and would be impossible to use.
History
Isaac Newton made the connection between what keeps the planets rotating around the Sun and what keeps us standing on the Earth. In 1687, when the Principia was published, Newton noted that the force that held the planets on their orbits, and the force that kept the moon on its orbit around the Sun, must be the same.
Through Newton's theory, the existence of Neptune was predicted and subsequently confirmed.
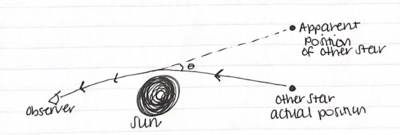
As we know now, however, there are some slight discrepancies between observations and Newton's theory that couldn't be explained prior to the work of Albert Einstein. These discrepancies could, primarily, be noted in Space. One of these, for example, was an issue that arose in the way that Mercury's orbit changed over time. Simply put, there were some perturbations in the orbit that simply could not be explained by Newton's theory of gravity. This issue was first noted in 1859 by Le Verrier (who had also used gravity to predict the existence of Neptune, in fact). These precessions would not be fully explained until the early twentieth century (1915ish) when Albert Einstein first proposed the theory of relativity. Furthermore, the deflection of light around massive bodies such as the Sun, as can be seen in the diagram to the right, although somewhat predicted by Newton's theories, occurred to a much greater degree than Newton had predicted. However, these discrepancies were perfectly in accordance with general relativity. It was in 1919 that Eddington measured these deflections.
See Also
- This link provides a general timeline of gravity, and dives into some basics of relativity with helpful diagrams.
- Here, one can find a helpful article detailing how GPS Systems are, in fact, proof of the concept of general relativity.
- A general overview of the history of gravitational theory.
- Hyperphysics page describing a general overview of gravity.