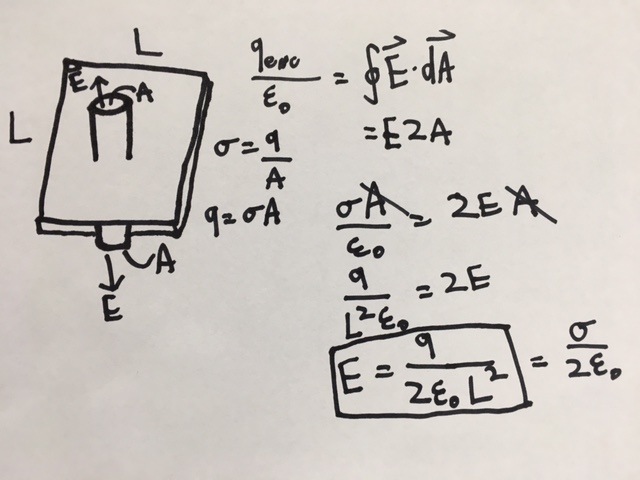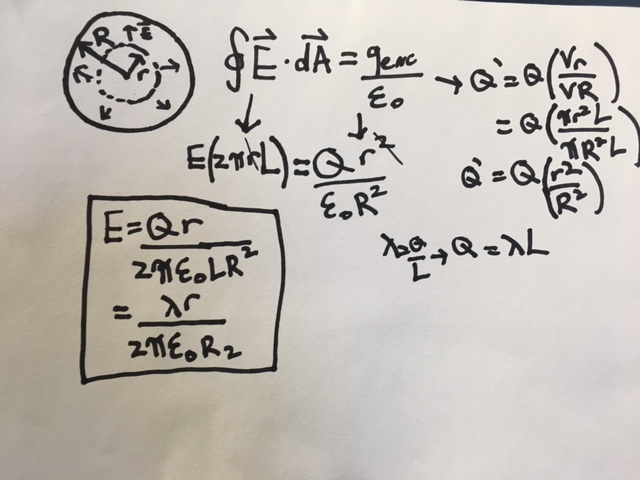Gauss's Flux Theorem

Claimed by Courtney Smith (Fall 2018) Edited by Alex Casado (Spring 2019) Edited by Anna Seppings (Spring 2019) Edited by Robbie van Zyl (Spring 2020)

The Main Idea

Gauss's Flux Theorem describes the relationship between the charges inside of an object and the electric field acting on the surface(s) of that object. This theorem makes it possible to determine the sum of total charges inside an object; by calculating the direction and magnitude of all electric fields acting on an object, you can use a ratio to determine the charges inside that object. There is a proportional relationship between electric fields acting on an object and the charges inside that object, and that ratio is shown below in the Mathematical Model section. This relationship applies to all shapes with any number of sides, as long as the object is enclosed.

Note that Gauss's Flux Theorem only tells you the relationship between electric fields outside an object and the charges inside an object. It does not tell you anything about the charges outside of the object. Therefore, any outside charges do not affect Gauss's Flux Theorem calculations. This is because Gauss's Law uses the superposition principle. So no charges outside the object will produce any electric field (and in turn, zero electric flux) acting on the object.

Essentially, electric flux can be thought of as the flow rate of the electric field through a given area.

Gauss's Law Analogous Model

Shown below is an analogous example to help understand gauss's law and electric flux:

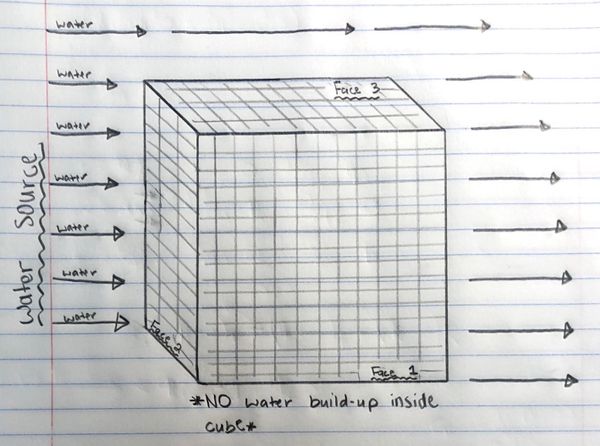
At the center of the image, you can see a 3-dimensional cube comprised of mesh faces and a water source going from left to right across the page. The mesh on each of the faces of the cube ensures that only water flowing normal to the screen surface(perpendicular to the face of the surface) will enter/exit the cube. Notice that in the image the water flowing into the face on the left (labeled Face 2) is normal to the face, therefore flowing into the box and filling it up while the water passing parallel to the top face (labeled Face 3) is flowing along the top surface of the box but does not enter the cube. One may also realize that the sum of the water entering/exiting of each of the faces of the cube at any moment in time is the net volume of water sitting in the mesh cube at this moment in time. With that being said, it becomes clear that in this scenario that there is no build-up of water in the mesh cube because the water flowing into the left side face (Face 2) flows directly back out the right side face(not shown) and the other 4 faces do not have water entering/exiting them.

Electric flux in gauss's law functions analogously; the flowing water represents the electric field and the mesh box represents the object of interest. When the electric field is perpendicular to a given surface the field enters the object and contributes to the flux while an electric field parallel to a face of the object does not enter the object and does not contribute to the total flux. Furthermore, if the field flows through the object from one face to another, then the net flux of these two sides is zero because the field entering on the one side is canceled out by the field exiting on the other side. Just as the sum of the water entering each face yields the volume of water inside the cube, the sum of the flux from each surface (field perpendicular to the surface) yields the next flux entering and exiting the object of interest (in the case of this example it would be zero).

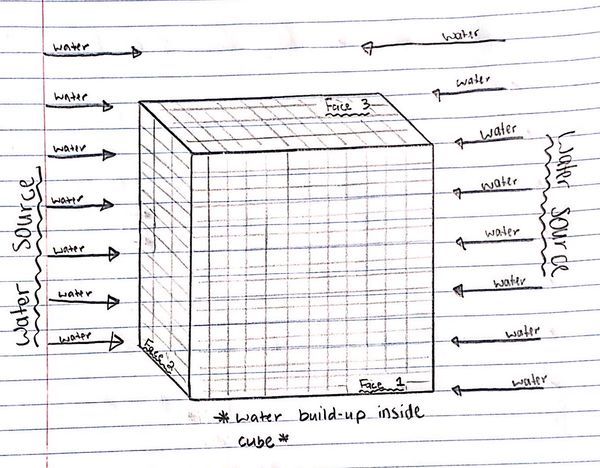
In another example shown above, the water flow is flowing towards the cube from both the left and the right. Applying the same principles as above where only water flowing perpendicular to a face enters the said face, it becomes clear that water is, indeed, filling up inside the mesh cube because water is entering through the left face (labeled Face 2) while water is also entering through the right face. Unlike the analogy above where there was no net water inside the cube, this example would have a positive flux because there is water building up inside the cube.

A Mathematical Model

The electric flux of a closed object is equal to the total charge enclosed over the permittivity of free space constant (epsilon naught). The electric flux of a closed surface is also equal to the surface integral of an electric field evaluated over the object's surfaces.

[math]\displaystyle{ \Phi_E = \frac{\Sigma q}{\varepsilon_0} = \oint_C E\bullet \hat{n} dA }[/math]

Where E is the electric field, dA is the infinitesimal area in the direction of the electric field, [math]\displaystyle{ \hat{n} }[/math] is the unit normal vector, sigma q is the sum of the charges inside the closed surface, and the dot denotes a dot product.

For the special case of a constant electric field, the electric flux is equal to the electric field multiplied by the area and the cosine of the angle between the two vectors.

[math]\displaystyle{ \Phi_E = EAcos(\theta) }[/math]

Where E is the electric field, A is area of the surface, and [math]\displaystyle{ \theta }[/math] is the angle between the E and A. Note that this is the electric flux for one side of an object. If you want to know the electric flux of the total object, you must use this formula for calculating flux on each side of the object.

Gaussian Surface

To find the electric field and charge enclosed of different shapes and surfaces, often times a Gaussian surface must be drawn that encompasses a part of the main surface. When trying to find the electric field at a point outside of the surface at hand, a surface including the point should be drawn. The Gaussian surfaces are usually spheres or cylinders, although it usually doesn't matter in the end as the area of the Gaussian surface will cancel out. Spheres are used when one is trying to find the electric field of a point charge, a spherical shell of uniform charge, or any other object with a symmetric charge distribution. A cylinder should be used as the Gaussian surface when one is trying to find the electric field of an infinitely long line of charge, and infinite plane or sheet of charge, or a cylinder of charge. When analyzing the Gaussian surface, only the surfaces where the normal vector of the area is not perpendicular to the electric field vector should be considered for calculations. When trying to find the electric field of a shape inside of the total object, finding the ratio of volumes and multiplying that by Q enclosed should be done to find the charge of the smaller object.

It is important to note that when using a gaussian surface any charge outside of the surface creating a field has no effect on the calculation of flux. Only charge within the gaussian surface and the electric field due to these charges are taken into account when calculating flux.

A Computational Model

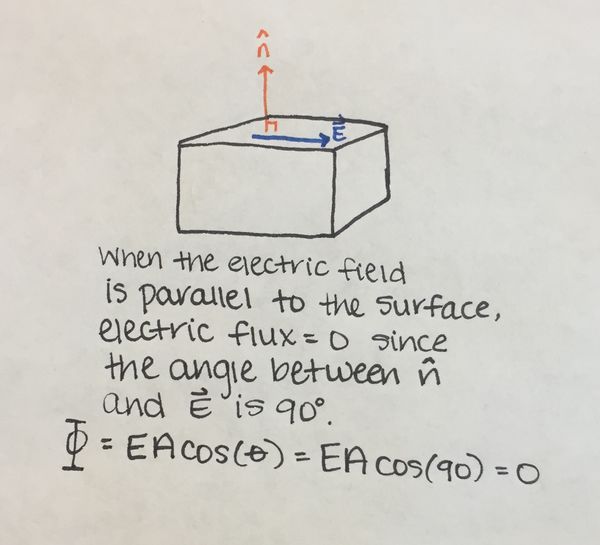
Gauss's Flux Theorem is able to be visualized by observing the direction and angle of an electric field traveling through a given surface. Typically in Gauss's Flux calculations, you are concerned with two vectors: n-hat and the electric field vector. N-hat always points perpendicular from the surface of interest, while the electric field can point in any direction and will vary from problem to problem. It is always important to note the angle between the n-hat vector and the electric field. If that angle is perfectly perpendicular, the contributed electric flux will be zero.

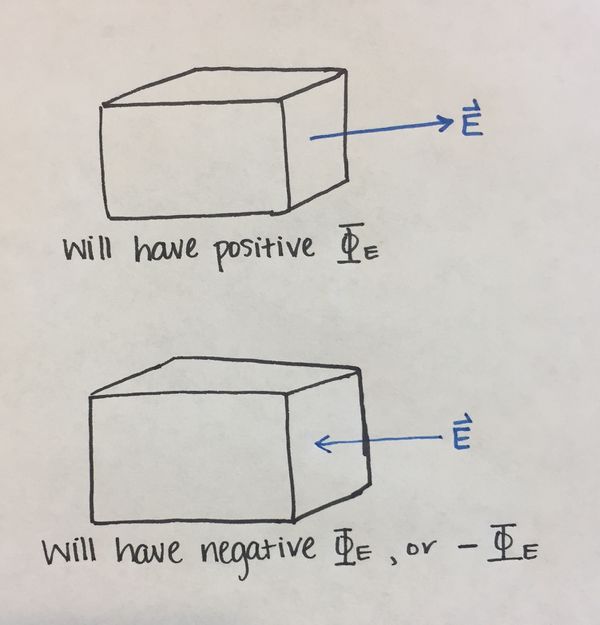
It is also important to note the sign (positive or negative) of the electric flux, with respect to the direction of the electric field. If the electric field is pointing into the surface, the flux will be negative. If the electric field is pointing out of the surface, the electric flux will be positive.

Examples

Easy

One Surface and Uniform Electric Field

A disk of radius 5 centimeters is in an area of uniform electric field with magnitude 400 Volts/Meter. The angle between the electric field and the disk is 35 degrees.

Using the simplified version of Gauss's Law because the electric field is uniform: [math]\displaystyle{ \Phi_E = EAcos(\theta) }[/math], fill out the known values, which in the case is all values needed.

[math]\displaystyle{ \Phi_E = (400)(\pi0.05^2)cos(35) }[/math]

[math]\displaystyle{ \Phi_E = 2.573 }[/math] Volt Meters

Middling

Multiple Surfaces and Uniform Electric field

An equilateral prism lies on top of a rectangular prism with dimensions l = 5cm, w = 7cm, h = 19cm, and is in an area of uniform electric field with magnitude 560 Volts/Meter perpendicular to the long sides of the rectangular prism.

Using the simplified version of Gauss's Law because the electric field is uniform: [math]\displaystyle{ \Phi_E = EAcos(\theta) }[/math]

First of all it is important to note that there are four surfaces that contribute to the net electric flux. two of the two long sides of the equilateral prism and two of the long sides of the rectangular prism. We know the angles between E and A because the top prism is an equilateral triangle, so all the side angles are 60 degrees. With this equation we can write:

[math]\displaystyle{ \Phi_E = E[(w*h)cos(120) + (w*h)cos(60) + (w*h)cos(180) + (w*h)cos(0)] }[/math]

[math]\displaystyle{ \Phi_E = 0 }[/math]

Difficult

Non-Uniform Electric Field

A solid sphere of radius R has a charge +Q uniformly distributed throughout. Find the Electric field at locations r1<R.

For this problem we can utilize the equality of [math]\displaystyle{ \frac{Q}{\varepsilon_0} = \oint_C E\bullet dA }[/math]

For r1<R, we know the line integral of dA is just the circumference of the gaussian surface we took, a sphere of radius r1.

[math]\displaystyle{ \frac{Q}{\varepsilon_0} = E\bullet 4\pi r_1^2 }[/math]

Since we're taking a portion of the sphere we need to find the portion of the charge that is inside of the Gaussian surface. In order to find the charge of the smaller sphere, we divide the total charge by the total volume to get the charge per unit volume. We then multiply that value q by the volume of the smaller sphere (radius r1) to get the charge contained in that volume.

The work is shown below.

[math]\displaystyle{ q = \frac{3Q}{4\pi r_1^3}*\frac{4\pi R^3}{3} }[/math]

[math]\displaystyle{ q = Q\frac{r_1^3}{R^3} }[/math]

[math]\displaystyle{ E = Q\frac{r_1}{4\pi R^3} }[/math]

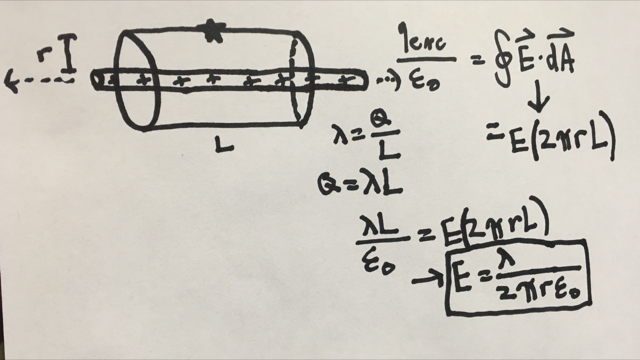
Electric Field of Infinite Line Charge

What is the electric field on a point from an infinitely long line charge?

For this problem, the Gaussian surface we use is a cylinder encompassing a portion of the wire.

For this problem, we can use the Gauss's law to relate the enclosed charge and electric field of the wire: [math]\displaystyle{ \frac{Q}{\varepsilon_0} = \oint_C E\bullet dA }[/math]

For the left side of the equation, the linear charge density can be applied to ultimately replace Q:

[math]\displaystyle{ {\lambda} = Q/L }[/math]

[math]\displaystyle{ Q = {\lambda}L }[/math]

So, the left side of the equation simplifies to: [math]\displaystyle{ \frac{{\lambda}L}{\varepsilon_0} }[/math]

On the right side of the equation, E can be taken out of the integral and dA is replaced with the surface area of the curved portion of the cylinder, which is the gaussian surface:

[math]\displaystyle{ \oint_C E\bullet dA = E(2{\pi}rL) }[/math]

From here, the two simplified versions of each side of the equation can be combined: [math]\displaystyle{ \frac{{\lambda}L}{\varepsilon_0} = E(2{\pi}rL) }[/math]

Finally, through algebraic manipulation, E is found to be: [math]\displaystyle{ E = \frac{{\lambda}}{2{\pi}r{\varepsilon_0}} }[/math]

Electric Field of Sheet of Charge

What is the electric field on a point above a sheet of charge?

For this problem, the Gaussian surface is a cylinder going through both sides of the sheet.

First Gauss's law can be applied: [math]\displaystyle{ \frac{Q}{\varepsilon_0} = \oint_C E\bullet dA }[/math]

On the left side of the equation, the 2D charge density can be used to replace Q:

[math]\displaystyle{ {\sigma} = \frac{q}{A} }[/math]

[math]\displaystyle{ q = {\sigma}A }[/math]

On the right side of the equation, the statement [math]\displaystyle{ \oint_C E\bullet dA }[/math] can be replaced by [math]\displaystyle{ 2EA }[/math]. The 2 is included because the electric field going out the bottom must be accounted for.

From here, after combining both sides of the equation, we get: [math]\displaystyle{ \frac{{\sigma}A}{\varepsilon_0} = 2EA }[/math]

Next, the A on each side cancels out, and we can isolate E to find the final solution: [math]\displaystyle{ E = \frac{{\sigma}}{2{\varepsilon_0}} }[/math]

This answer can also be left in terms of q and Area. In this case, the dimensions of the sheet are LxL, so area can be replaced by [math]\displaystyle{ L^2 }[/math]: [math]\displaystyle{ E = \frac{q}{2{\varepsilon_0}L^2} }[/math]

Electric Field inside Cylinder of Charge

What is the electric field at a point inside of a cylinder of charge?

For this problem, we can create a Gaussian surface of a smaller cylinder inside the larger one. From here, we can first use Gauss's Law: [math]\displaystyle{ \oint_C E\bullet dA = \frac{Q}{\varepsilon_0} }[/math]

For the left part of the equation, E can be brought out of the integral and dA is replaced with the curved surface area of the inner cylinder:

[math]\displaystyle{ \oint_C E\bullet dA = E(2{\pi}rL) }[/math]

For the right side of the equation, Q for the smaller Gaussian surface can be found by multiplying the charge of the larger cylinder by the ratio of volumes:

[math]\displaystyle{ Q' = Q(\frac{Vr}{VR}) = Q(\frac{{\pi}r^2L}{{\pi}R^2L}) = Q(\frac{r^2}{R^2}) }[/math]

Next, both sides of the equation can be combined to form a new equation: [math]\displaystyle{ E(2{\pi}rL) = \frac{Qr^2}{{\varepsilon_0}R^2} }[/math]

From here, the r on the left side of the equation and one r from the right side cancel out. Finally, we can isolate E to find the electric field:

[math]\displaystyle{ E = \frac{Qr}{2{\pi}{\varepsilon_0}LR^2} }[/math]

This answer can also be in a different form if the linear charge density is used: [math]\displaystyle{ {\lambda} = \frac{Q}{L} }[/math]

Finally, the [math]\displaystyle{ \frac{Q}{L} }[/math] can be replaced by [math]\displaystyle{ {\lambda} }[/math] in the electric field equation:

[math]\displaystyle{ E = \frac{{\lambda}r}{2{\pi}{\varepsilon_0}R^2} }[/math]

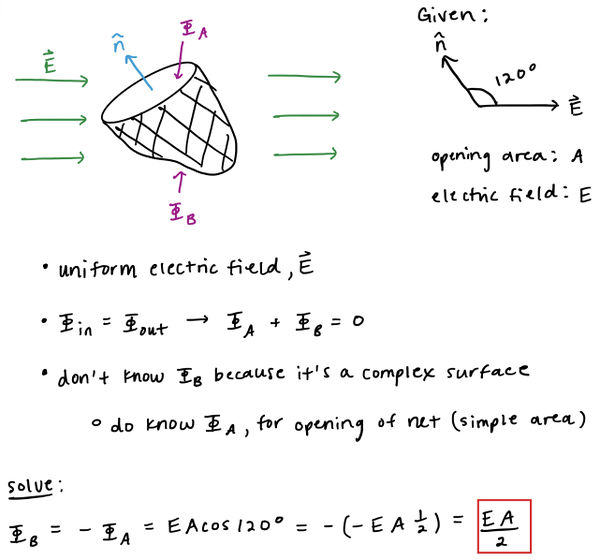
Complex Surface

For this problem, we are asked to use Gauss's Law to determine the flux of a net.

Multiple Charges/Objects

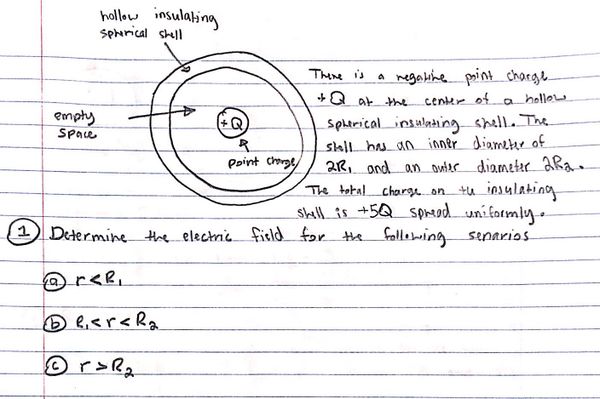
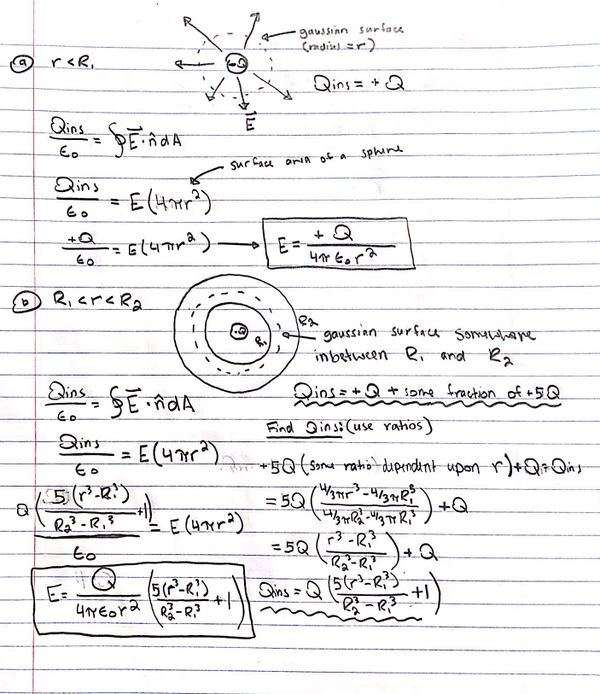
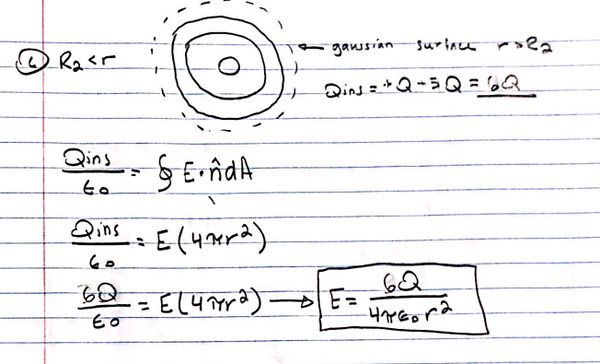
One of the most challenging kinds of problems for gauss's law is when one is asked to find either the electric flux, electric field, or charge inside a given gaussian surface or enclosed volume. In the following example, I am going to calculate the electric field at a specified radius r using gauss's law and my knowledge regarding the law:

Above are the question description and a supporting diagram. Notice that the first and third cases will be relatively easy because the radius of our gaussian surface(r) does not fall partially within a charged object. The second case is far more complex because the radius of the gaussian surface includes some portion of the charge from the spherical shell.

Let's jump into some algebra:

The key to solving the second case was to realize that the amount of 4Q included in the gaussian surface can be found using a ratio describing how much volume the gaussian surface includes out of the total volume of the spherical shell. The ratio ended up looking something like this: (volume up till r - volume of space up to R1) / (volume up to R2 - volume of space up to R1 ) and you multiply this ratio by 4Q and then subtract Q(center charge) to get the total charge inside the gaussian surface.

And case three to round it up:

Differential Form

Coulomb's law has a critical flaw when it comes to calculating the electric field at some location near a quick-moving charge. This problem called Relativistic Retardation occurs at pretty much all occasions, unless the charge is not moving at all or moving extremely slow as compared to the speed of light. Relativistic Retardation is due to the fact that the electric field calculation depends on the origin of a charge (i.e. the location where it started moving), not the current location of the charge. So if the charge has moved from its starting location, then the electric field calculation is wrong in Coulomb's law, which also means that it is inconsistent with the theory of special relativity.

Gauss's Law does not have this critical flaw and is consistent with relativity due to a property called Divergence. Conceptually, Divergence is a way to measure electric fields at some point in time as compared to a source charge at that same point in time; so the property of Divergence is the reason that Gauss's Law does not experience Relativistic Retardation. Divergence is defined as the amount of electric flux in an object as the limit of that object's volume goes to zero.

The formula which expresses divergence is called The Differential Form of Gauss's Law:

[math]\displaystyle{ \nabla \cdot \mathbf{E} = \frac{\rho}{\varepsilon_0} }[/math]

where the del is the differential operator, E is the electric field vector, rho is the electric charge density, the constant epsilon naught is the electric permittivity of free space, and the dot denotes a dot product.

Connectedness

Most of the applications of Gauss's Law include finding the electrical fields of different shapes or the charges inside those shapes. Gauss's Law can be applied to a variety of objects such as a sphere, sheet of charge, and cylinder. This use of Gauss's Law is especially helpful in the field of Physics. Furthermore, the use of electric flux in Gauss's Flux Theorem assists in studying and understanding Faraday's Law and its applications to objects such as electrical generators, transformers, and inductors.

Being an industrial engineer, Gauss's Law is particularly interesting to me. It proportionally relates electric field to charge within an object. Industrial engineering deals with a lot of probability and numerical methods, so proportionality relationships really interest me and help when understanding the "big-picture" of a concept. It is relatively intuitive to think that electric fields and interior charges would some-how be related, but being able to actually quantify that relationship through Gauss's Law is very important and interesting.

History

Friedrich Gauss was born in 1777 in Brunswick, Germany. He was an extremely intelligent child, many considered him a prodigy. In fact, he discovered the exact date of his birthday by solving a puzzle about his birthdate in the context of the date of Easter and deriving methods to compute past and future dates. He started making mathematical computations and discoveries in his teen years. And in 1835, he formulated Gauss's Law as a different way to derive Coulomb's Law. He made many other discoveries in the fields of mathematics, statistics, probability, and number theory.

Today, Gauss's Law remains as one of Maxwell's equations, which are the four equations that make up classical electrodynamics. Maxwell's four equations are Gauss's Law for electricity, Gauss's Law for magnetism, incomplete version of Faraday's Law, and Ampere's Law. In addition to discovering Gauss's Law for Electricity and Gauss's Law for magnetism, Gauss also discovered other physics laws and equations including a method for measuring the horizontal intensity of the Earth's magnetic field and a mathematical theory for separating the inner and outer sources of the Earth's magnetic field.

http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elesht.html

http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elecyl.html