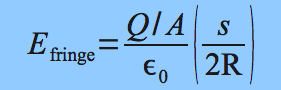Charging and Discharging a Capacitor

[1] The main purpose of having a capacitor in a circuit is to store electric charge. For intro physics you can almost think of them as a battery.

Edited by ROHAN NANDAKUMAR (SPRING 2021)

The Main Idea

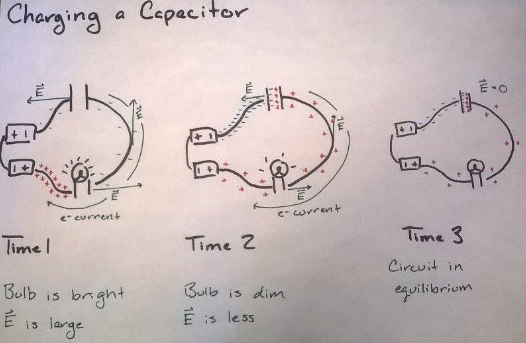
Charging a Capacitor

Charging a capacitor isn’t much more difficult than discharging and the same principles still apply. The circuit consists of two batteries, a light bulb, and a capacitor. Essentially, the electron current from the batteries will continue to run until the circuit reaches equilibrium (the capacitor is “full”). Just like when discharging, the bulb starts out bright while the electron current is running, but it slowly dims and goes out as the capacitor charges.

The electron current will flow out the negative end of the battery as usual (conventional current will exit the positive end). Positive charges begin to build up on the right plate and negative charges on the left. The electric field slowly decreases until the net electric field is 0. The fringe field is equal and opposite to the electric field caused by everything else.

If you were to draw a box around the capacitor and label it with positive and negative ends it would look like a battery. It also behaves like a battery. The electron current will continue to flow and the electric field will continue to exist until the potential difference across the capacitor is equal to that of the batteries (sum of emf of all batteries in the circuit).

The following link shows the relationship of capacitor plate charge to current: Capacitor Charge Vs Current

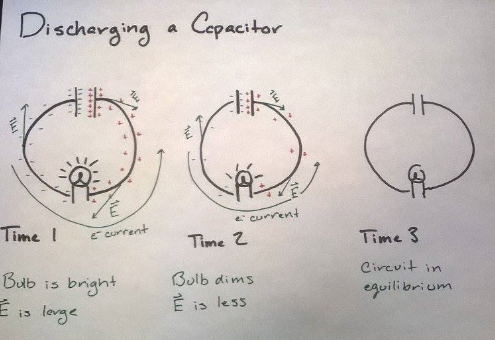
Discharging a Capacitor

A circuit with a charged capacitor has an electric fringe field inside the wire. This field creates an electron current. The electron current will move opposite the direction of the electric field. However, so long as the electron current is running, the capacitor is being discharged. The electron current is moving negative charges away from the negatively charged plate and towards the positively charged plate. Once the charges even out or are neutralized the electric field will cease to exist. Therefore the current stops running.

In the example where the charged capacitor is connected to a light bulb you can see the electric field is large in the beginning but decreases over time. The electron current is also greater in the beginning and decreases over time. Because of this the light bulb starts out shining brightly but slowly dims and goes out.

RIVASH DEEPNARAIN (SPRING 2023):

Determining Which side of the Capacitor becomes Positive and Negative

A common thing that confused me was which side of the capacitor acquires a positive charge and which side is negative. You need to know this because when calculating the voltage across a capacitor, you need to know whether your path goes against the electric field or in the same direction as the electric field that is in between the two plates. Since conventional current, denoted with a capital I, is actually the flow of positive charges, the side that the current meets first will therefore become positive. The other side would then become negative. Examples of this can be seen in the images below. This was confusing to me at first but after I realized this, calculating voltage across capacitors became much simpler.

Resistors

The amount of resistance in the circuit will determine how long it takes a capacitor to charge or discharge. The less resistance (a light bulb with a thicker filament) the faster the capacitor will charge or discharge. The more resistance (a light bulb with a thin filament) the longer it will take the capacitor to charge or discharge. The thicker filament bulb will be brighter, but won't last as long as a thin filament bulb. V = IR, The larger the resistance the smaller the current.

A Mathematical Model

[math]\displaystyle{ V = IR }[/math]

[math]\displaystyle{ E = (Q/A)/\varepsilon_0 }[/math]

[math]\displaystyle{ C = Q/V = \varepsilon_0A/s }[/math]

[math]\displaystyle{ V = (Q/A)s/ε0 }[/math]

A Computational Model

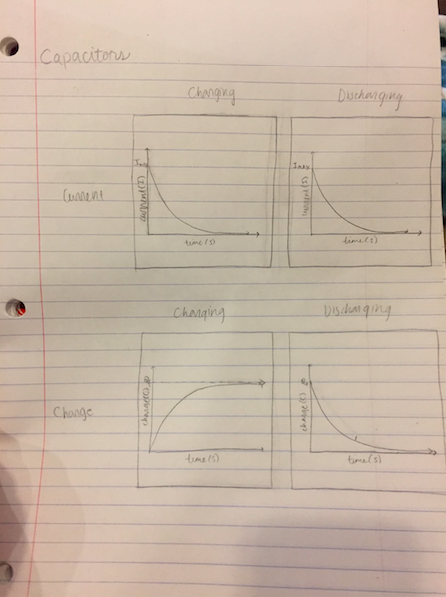
Current and Charge within the Capacitors

The following graphs depict how current and charge within charging and discharging capacitors change over time.

When the capacitor begins to charge or discharge, current runs through the circuit. It follows logic that whether or not the capacitor is charging or discharging, when the plates begin to reach their equilibrium or zero, respectively, the current slows down to eventually become zero as well.

When the plates are charging or discharging, charge is either accumulating on either sides of the plates (against their natural attractions to the opposite charge) or moving towards the plate of opposite charge. While charging, until the electron current stops running at equilibrium, the charge on the plates will continue to increase until the point of equilibrium, at which point it levels off. Conversely, while discharging, the charge on the plates will continue to decrease until a charge of zero is reached.

Time Constant

The time constant of a circuit, with units of time, is the product of R and C. The time constant is the amount of time required for the charge on a charging capacitor to rise to 63% of its final value. The following are equations that result in a rough measure of how long it takes charge or current to reach equilibrium.

[math]\displaystyle{ Q = (C\mathcal{E})[1−e^{(−t/RC)}] }[/math]

[math]\displaystyle{ I = (\mathcal{E}/R)[e^{(−t/RC)}] }[/math]

Note: [math]\displaystyle{ \mathcal{E} }[/math] is electromotive force(emf), whose units are Volts([math]\displaystyle{ V }[/math])

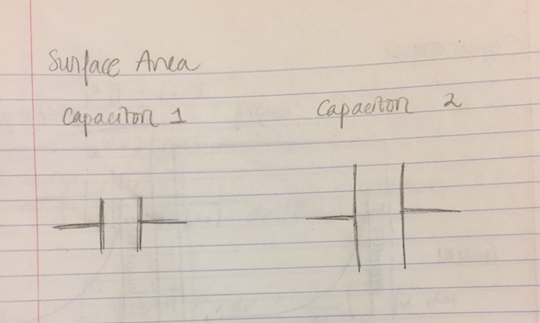
The Effect of Surface Area

For two different circuits, each with one of the above capacitors, the circuit with the second capacitor (with more surface area) has a current that stays more constant than the first. The larger capacitor also ends up with a greater amount of charge on its plates.

This is because fringe field magnitude is inversely proportional to plate area, as shown in the equation below. In the first, short time interval, roughly equal quantities of charge will accumulate on the capacitor plates. However, due to its greater area, capacitor 2 will have a weaker fringe field. This, in turn, results in a greater net field for that circuit. This greater net field results in more charge for that circuit compared to the other. More charge will be driven from the negative to the positive plate, and the drift speed changes less for capacitor 2 than capacitor 1.

The equation for fringe electric field is the following:

Examples

Question 1

Doubling the radius of the capacitor

A) quarters the capacitance

B) halves the capacitance

C) doubles the capacitance

D) quadruples the capacitance

Doubling the radius of the capacitor

A) quarters the electric field between the plates

B) halves the electric field between the plates

C) doubles the electric field between the plates

D) quadruples the electric field between the plates

Doubling the distance between the plates

A) quarters the capacitance

B) halves the capacitance

C) doubles the capacitance

D) quadruples the capacitance

Doubling the capacitance

A) quarters the electric field between the plates

B) halves the electric field between the plates

C) doubles the electric field between the plates

D) quadruples the electric field between the plates

ANS: D, B, A, C

Question 2

What is the current at points A,B, and C when the capacitor is not yet charged and when the capacitor is fully charged?

When the capacitor is fully charged what is the charge on the plates?

Answer:

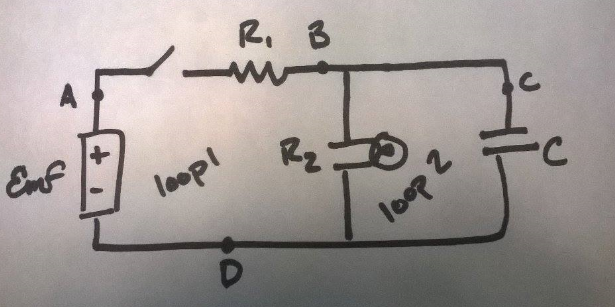
Question 3

The switch has been closed for a long time.

What is the current at each point?

What is the charge on the capacitor?

Is the light bulb lit?

The switch is opened.

Immediately after the switch is opened is the bulb lit? After a while?

What current is initially running through the bulb?

Which direction is the current moving?

Answer:

Connectedness

Capacitor can be temporary batteries. Capacitors in parallel can continue to supply current to the circuit if the battery runs out. This is interesting because the capacitor gets its charge from being connected to a chemical battery, but the capacitor itself supplies voltage without chemicals.

Capacitors are being researched for applications in electromagnetic armour and electromagnetic weapons. Currently capacitors are used as detonators in nuclear weapons. Capacitors also are largely involved in separations of AC and DC components.

History

Put this idea in historical context. Give the reader the Who, What, When, Where, and Why. In 1745 Ewald Georg von Kleist was the first to "discover" capacitors in Germany. He connected a generator to glass jars of water and charged them. When he touched the wire they were connected to he shocked himself (discharged the capacitor). At the same time Pieter van Musschenbroek made a similar capacitor and named it the Leyden Jar. When Benjamin Franklin studied the Leyden Jar he determined, among other things, that the charge was stored on the glass. During his studies Franklin was the first to give the capacitor the name battery. Since then batteries have most often been electro-chemical cells of capacitors made of sheets of conducting and dielectric material.

Charging and Discharging a Capacitor

Contents

The Main Idea

A Mathematical Model

A Computational Model

Current and Charge within the Capacitors

The Effect of Surface Area

Examples

Connectedness

History

See also

Further reading

External links

References

Navigation menu