Charged Disk
The Main Idea
The electric field of a charged disk can be imagined as the total electric field produced from each point on the disk. We can relate this the the Law of Superposition, but considering the disk as a collection of rings, which will lead to a better understanding of the electric feild produced by the disk. This is especially important because two oppositely charged metal disks collectively are known as a capacitor, a concept seen in several places in physics and the real world.
A Mathematical Model
Before we begin our calculations, take a look at this image of a uniformly charged disk:
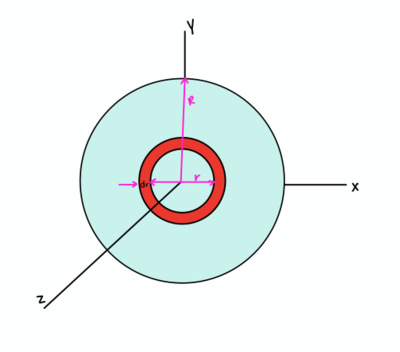
This image shows a visual representation of a disk. It should look pretty familiar. In fact, the shape of a disk is simply an extension of a ring. Think of it as infinitely many uniformly charged rings. Thinking of a disk this way will help to understand the equation of the electric field for a uniformly charged disk.
Recall the equation for the electric field of a uniformly charged ring:
[math]\displaystyle{ \ E= \frac{1}{4π\epsilon_0}\frac{qz}{(R^2+z^2)^{3/2}} }[/math]
This equation will tell you the electric field of a uniformly charged ring at any observation location z. To apply this equation to a disk, integration will be involved. The integration variable in this case should be the radius of the ring [math]\displaystyle{ r }[/math], as that will change with the infinitely many concentric rings you have. However, [math]\displaystyle{ r }[/math] is nowhere to be found in the equation. But if the radius of each ring is different, what gets affected as a result?
[math]\displaystyle{ \ dq = Q\frac{area of ring}{area of disk} = \frac{π((r+dr)^2-r^2)}{πR^2} = \frac{π(r^2 - r^2 +2r*dr+ dr^2)}{πR^2} }[/math]
We assume that [math]\displaystyle{ dr^2 }[/math] is essentially zero compared to the non-squared differential term.
[math]\displaystyle{ dq= Q\frac{2πrdr}{πr^2} }[/math]
Here you see that the charge of each ring is different due to the changing radius. The charge changes by a factor of the area of the ring, [math]\displaystyle{ 2πrdr }[/math], (if you roll out the ring, it is a rectangle with height [math]\displaystyle{ dr }[/math] and width [math]\displaystyle{ 2πr }[/math]) divided by the area of the disk, [math]\displaystyle{ πr^2 }[/math]. Plugging that in for the q variable in our integration, and then cancelling out some variables, will allow us to solve for the electric field of a disk:
[math]\displaystyle{ \ dE = \frac{1}{2\epsilon_0}\frac{Q}{πR^2}\frac{zrdr}{(R^2+z^2)^{3/2}} }[/math]
Now we take the integral of this equation, and the result is this:
[math]\displaystyle{ \ E = \frac{1}{2\epsilon_0}\frac{Q}{πR^2}[1 - \frac{z}{(R^2+z^2)^{1/2}}] }[/math]
Thus, we have the equation that finds us the exact electric potential of a uniformly charged disk. You can still make approximations to make the formula simpler, however. If your observation location z is very close to the disk but not touching it, and is also significantly smaller than the radius of the disk (i.e. [math]\displaystyle{ 0 \lt \lt z \lt \lt R }[/math]), the equation becomes this:
[math]\displaystyle{ \ E = \frac{Q}{2\epsilon_0A} }[/math]
This is the most commonly seen form of this equation, and becomes very important when applied to the case of capacitors. A key aspect of the field in these situations is the fact that it's constant in space between two charged plates. This unique aspect of capacitors, which does not occur for any other type of charged geometry, allows for several novel applications.
A Computational Model
The writers of the textbook Matter and Interactions 3rd Edition, have some great examples of VPython code that show, in computational form, the electric field of a uniformly charged disk. To see the code in action, take a look at this or copy the code into your VIDLE shell. Enjoy!
Also took a look at this java applet for a lab simulation of a capacitor
Examples
Simple
In what circumstance would you not use the approximate formula for calculating the electric field and have to use another formula?
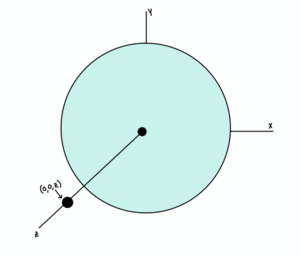
This question is important, as this situation can come up a lot when solving physics problem. Remember that in the special case [math]\displaystyle{ 0 \lt \lt z \lt \lt R }[/math], you are allowed to use the approximate formula. But if that second condition, [math]\displaystyle{ z \lt \lt R }[/math], is not true, then you must use the exact formula (listed above). Or, if [math]\displaystyle{ 0 \lt \lt z }[/math], you also must use the exact formula, as then the observation location is relatively far from the disk. So it is important to look at your [math]\displaystyle{ z }[/math] value when you decide which equation to use when finding the electric field of a uniformly charged disk.
Middling
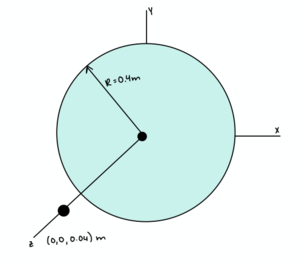
A thin plastic disk, with it's center on the origin, and a of radius 0.4 m is uniformly charged with charge [math]\displaystyle{ Q = -4 * 10^{-7} C }[/math]. What is the electric field of this disk at a location [math]\displaystyle{ \lt 0,0,0.04\gt }[/math]m?
This is a a pretty simple problem, as [math]\displaystyle{ 0 \lt \lt z \lt \lt R }[/math], so you can use the approximate formula:
[math]\displaystyle{ \ E = \frac{4 * 10^{-7}}{2\epsilon_0π*(0.4)^{2}} = 4.5 * 10^{4} N/C }[/math]
Difficult
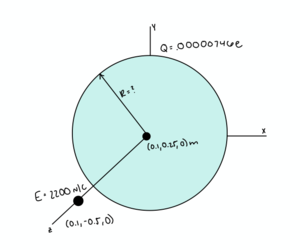
A thin plastic disk located with a center at [math]\displaystyle{ \lt 0.1, 0.25, 0\gt }[/math] m is uniformly charged with an excess of [math]\displaystyle{ 7.46 * 10^{-6} }[/math] electrons. Find the radius of the disk if it generates an electric field of [math]\displaystyle{ E = 2.2 * 10^{3} N/C }[/math] at a location of [math]\displaystyle{ \lt 0.1, -0.5, 0\gt }[/math] m?
Since we don't know the radius of the disk, we cannot be sure that using the approximation would be accurate, because we don't know if [math]\displaystyle{ z \lt \lt R }[/math]. We must use the full formula,
[math]\displaystyle{ E = \frac{1}{2\epsilon_0}\frac{Q}{πR^2}[1 - \frac{z}{(R^2+z^2)^{1/2}}] }[/math]
We start by calculating Q, knowing that [math]\displaystyle{ Q = e * -1.602 * 10^{-19} = -1.2 * 10^{-6} C }[/math]
Next, we find z, which is essentially the distance from the center of the disk to the observation point.
[math]\displaystyle{ z = mag( \lt 0.1, -0.5, 0\gt - \lt 0.1, 0.25, 0\gt ) = 0.75 }[/math]
Finally, we use the original equation for electric field to solve for R. [math]\displaystyle{ R = 2.6 }[/math] m. If we solve it using the approximated formula,
[math]\displaystyle{ E = \frac{Q}{2\epsilon_0A} }[/math]
We calculate [math]\displaystyle{ R = 3.13 }[/math], which has a significant amount of error from the original formula calculation. This indicates that using the approximation in this scenario would not have been appropriate.
Connectedness
Uniformly charged disks are a fundamental component to capacitors (which is two disks placed parallel to each other), which are found everywhere in physics courses as well as the real world. They are key parts of LC circuits, RC circuits, batteries, signal processing, and can even produce light.
Charged Disks in Television
Capacitors and charged plates used to play a heavy role in televisions! Charged plates were used to accelerate electrons, which were then manipulated and directed by magnetic fields to control what area of the television screen they would strike. As they hit the screen, a certain chemical would glow a specific color, generating an image. So every time you woke up early on saturday morning (before the advent of flat screen televisions), your episodes of Spongebob and Fairly OddParents was brought to you by capacitors!
Charged Disks in Chemical Engineering
The electric fields of capacitors may seem completely unrelated to chemical engineering. But actually, there are a surprising number of applications within chemical engineering. For example, much of the instrumentation used in chemical processes rely on capacitors and their ability to generate constant electric fields between two charged plates.
Industrial Applications
One of the primary careers in chemical engineering focuses on operating, maintaining, and optimizing a chemical plant or refinery. In a refinery, there are thousands of things you have to monitor throughout the plant. Every pipe and vessel holding liquid or gas is susceptible to corrosion, and any breach in containment could jeapordize thousands of lives. One of the most common causes of corrosion is ionic contaminants in water. Before a method was found to monitor and troubleshoot the ion concentrations in water, there were numerous dangerous corrosion events that put people's lives in danger.
Now, we monitor the conductivity of water in a refinery. This is done using CAPACITORS. Essentially, capacitors are used to monitor the changing electric field and dielectric properties of the water running through it. This data is then analyzed to find the amount of ionic contaminant in the water, allowing the chemical engineer to prevent corrosion at the source.
History
The first capacitor was invented in 1746. It was called the Leyden Jar, and it was essentially a glass jar wrapped in aluminum on both sides. They were used initially to store charge, almost as a battery. With the advent of radio technologies, capacitors played a key role in producing and receiving radio signals. Thus, they were heavily improved due to the demand from the radio industry.
As technology progressed, capacitors were developed that were smaller and more compact, allowing broad uses and applications. These ranged from diverse circuits to incredibly powerful transmitters.
See also
Further reading
External links
References
- Note: all images were created by author