Applying Magnetic Force to Currents
Claimed by Adam Zhang
Magnetic forces are forces that are exerted by a magnetic field on a moving charge, relative to the observation point. Because of this, currents exhibit magnetic forces on each other as they propogate moving charges.
The Main Idea
Given an understanding of the basics of how a magnetic field can exert a force on a moving charge, we can expand that to model how a magnetic field may affect a current as well as how multiple currents or moving charges may affect each other.
A Mathematical Model
First, we must determine the force exerted on a long, straight wire carrying current I by a uniform magnetic field. Given the equation for magnetic force, as per the following:
[math]\displaystyle{ {\vec{F} = q\vec{v}\times\vec{B}} }[/math]
We can assume that the wire will not experience any force if the current, or moving charge, is parallel to the magnetic field; however, if the magnetic field were perpendicular, or any orientation that were not parallel, a force on the wire or current may be expected. It is important to note that any current within the magnetic field may experience a force, but current outside the field may not.
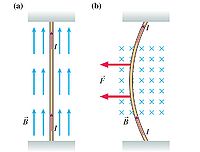
In deriving the exact equation relating magnetic force to current, current I can be related to moving charge q as it travels through a wire. By this logic, current can be equated to the amount of moving charge in a length of wire divided by the time the charge travels. This can be denoted by the following equations:
[math]\displaystyle{ {q = Idt = \frac{I\vec{l}}{\vec{v}}} }[/math]
[math]\displaystyle{ { {qv} = {Il} } }[/math]
Therefore, recalling the equation for magnetic force, we can derive the following:
[math]\displaystyle{ {\vec{F} = I\vec{l}\times\vec{B}} = {IlB}{sin\alpha} }[/math]
where [math]\displaystyle{ {\alpha} }[/math] is the angle between the magnetic field and the direction of the moving charges.
Now, we may consider two wires next to each which may create magnetic fields affecting both wires. To do so, we may assume wires with length l and distance d such that the following simplification for the magnetic field of a wire may be used:
[math]\displaystyle{ B = \frac{\mu_0I}{2d\pi} }[/math]
The following diagram will be referenced and modeled:
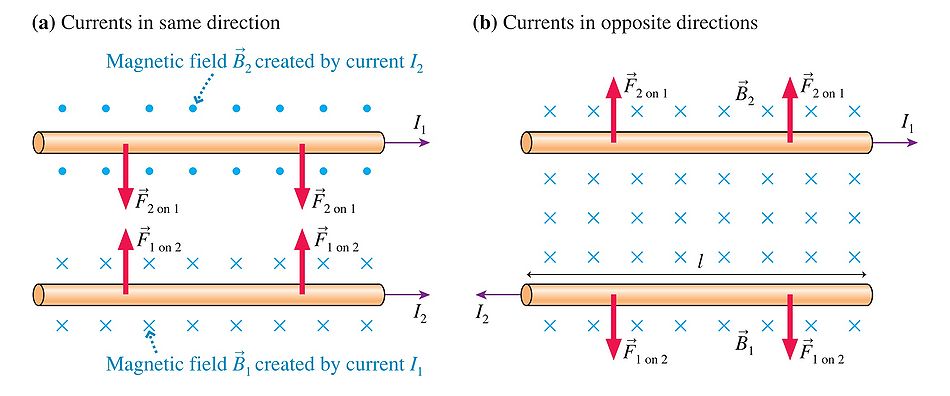
If it is first assumed that two wires have parallel currents running in the same direction. It can be observed that, due to the right hand rule, both wires cause a magnetic force toward each other. The bottom wire, I_2, causes a magnetic field, B_2, that exerts a downward force on the upper wire, I_1, and vice-versa.
If it is assumed that the wires have currents running in the opposite direction, the same logic can be used to find that each wire exerts a force away from each other; the wires cause a magnetic field that affects the other wire.
We can use this logic to find the force the bottom wire exerts on the top wire, relating both currents and distance:
[math]\displaystyle{ {\vec{F} = I_1\vec{l}\times\vec{B_2}} }[/math]
[math]\displaystyle{ {\vec{F} = {I_1}{\vec{l}}\frac{\mu_0I}{2d\pi}} }[/math]
It is important to note that this demonstrates only the force of one wire on another; total force between the two must be found by summing both forces from both currents.
Interesting notes can also be made regarding the magnetic field of the system. Observe that, when the currents run in the same direction, there is an effective net magnetic field of zero between the wires. This is because the wires, assuming equal magnitudes of current, cause equally opposing magnetic fields at that point.
See also
Magnetic Force
Magnetic Field of a Long-Straight Wire
Further reading
http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/forwir.html
http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/magcur.html
http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/forwir2.html
External links
References
Physics for Scientists and Engineers, 3rd Ed. By Randall D. Knight