Young's Modulus
This page discusses Young's Modulus, best described as the stiffness of a material, examples/problems involving this concept, and its numerous real-world applications. (Claimed by Sanjana Kapur; Fall 2017)
The Main Idea
Young's Modulus is a macroscopic property of a material that measures the stiffness of a solid material. It is independent of size or weight of the material, and it will change depending on the type of material for which the Young's Modulus is being measured. The uses of Young's modulus extend to two main sets of relationships, macroscopic springs and microscopic springs. In the case of macroscopic springs, Young's modulus is a measure of the stretchiness of a solid material outside of considerations of size and shape. In microscopic strings, when a solid object is modeled as a system of balls (atoms) connected by springs (an image of which can be seen as the cover image of the physics textbook Matter and Interactions I 3rd Edition), the Young's modulus constant of the material can be used to determine the 'interatomic spring stiffness' constant Ksi of a material in order to determine the stiffness and stretchiness of interatomic bonds. The SI unit of Young's Modulus is the pascal (Pa or N/m^2 or kg. m. s^−2).
A Mathematical Model
Mathematically, the Young's Modulus is the ratio of the stress placed upon a material to the strain that it endures. The definition of Young's Modulus can be expressed as: [math]\displaystyle{ {Y = \frac{stress}{strain}} = \frac{\frac{{F}_{T}}{A}}{\frac{{ΔL}}{L_o}} }[/math] where [math]\displaystyle{ {F}_{T} }[/math] is equal to the tension force, [math]\displaystyle{ A }[/math] is equal to the cross sectional area, [math]\displaystyle{ ΔL }[/math] is equal to the change in length due to the tension force, and [math]\displaystyle{ L_o }[/math] is equal to the initial length of the material.
Young's Modulus can also be expressed as: [math]\displaystyle{ {Y = \frac{Ksi}{d}} }[/math] where Y is the Young's modulus of the material being examined, Ksi is the value that represents the interatomic bond stiffness (how much a bond between two atoms will stretch), and d is the distance from the center of one atom to the center of another atom.
A Computational Model
- The following program calculates the microscopic and macroscopic Young's Modulus of a material. The source of this model is: https://trinket.io/python/8f0b71cda5
import math
element =raw_input("What element are you investigating? This will calcuate macro and microscopic Young's Modulus based on an example in Matter & Interactions 3rd Ed")
print element
print "mol=" ,6.02e23, "atoms"
ma = raw_input("What is the hanging mass in kilograms?")
print "ma=", ma,"kg"
ma=float(ma)
rho = raw_input("What is the density in kg/meters-cubed?")
print "rho=", rho, "kg/m^3"
rho=float(rho)
ama=raw_input("what is the atomic mass in kilograms?")
ama=float(ama)
print "ama=atomic mass", ama ,"kg"
mol =6.02e23
print
print "calculations"
vol=(ma/rho)
print "ma/rho=volume=",vol, "m^3"
print "total number atoms = N = rho*(mol/ama)", rho*(mol/ama)
N=rho*(mol/ama)
print "edge of 1m cube, number of atoms=", math.pow(N, 1/3)
atoms= math.pow(N, 1/3)
print
print "in one meter of atoms there are =", math.pow(N, 1/3), "atoms"
diam=1/atoms
print "the diameter of one copper atom =", diam,"m"
print
#print "one atom =", atoms/1, "meters"
print "Finding the spring constant of an interatomic bond"
print
print "data"
L =raw_input("how long is the wire in meters?")
L =float(L)
print "L=length of original wire", L, "m" #length of the wire originally
S=raw_input("what is the change in length in mm")
S=float(S)
print "S=change in length when weight is hung from the wire", S, "mm" #length of stretch
Sm=(S/1000)
print "S in meters", Sm, "m"
print
print "cacluations"
print "Ks= macro spring constant for wire=weight/distance"
M=10
print "M= mass placed on the wire =", M,"kg"
weight=M*9.8
print "weight =", M*9.8, "N"
print "Ks = Weight/change in length", (M*9.8)/S,"N/m"
Ks=(M*9.8)/S
print "NL=Number of Atoms in one chain length", L/(1/atoms), "atoms"
NL=L/(1/atoms)
w=raw_input("width of the wire in millimeters?")
w =float(w)
d=raw_input("depthof the wire in millimeters?")
d = float(d)
print "w=width of rectangular wire=", (w/1000), "m"
wm=w/1000
print "d=depth of rectangular wire=", (d/1000), "m"
dm=d/1000
A=wm*dm
print "A = area of the wire", A, "m^2"
Aa=diam*diam
print "Aa = area of an atom", Aa, "m^2"
NA=(A/Aa)
print "NA=Number of atoms in a cross-sectional area of wire",NA,"atoms"
print "Km= interatomic spring constant for copper"
print "Ks=((Km*NA)/NL)"
Km=(Ks*NL)/NA
print "Km =((Ks*NL)/NA)",Km ,"N/m"
YMmac=((weight/A)*(L/S))
print "Young's Modulus: Macroscopic = (Force tension*wire length)/(wire area*change in length due to wieght", YMmac, "Pa"
YMmicro=Km/diam
print "YMmicro=Microscopic Spring Constant/atomic diameter"
print "Young's Modulus:Microscopic", YMmicro, "Pa"
The following image demonstrates the concept of Young's Modulus. A force causes a solid material to stretch by a constant certain amount. This relationship is named Young's Modulus and is independent of mass of the object, and varies based on material.
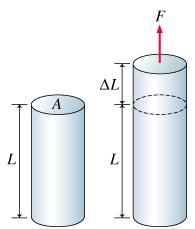
Examples
Simple
Example 1. A cylinder of wood has a stress of 800 and a strain of [math]\displaystyle{ 8*10^-7 }[/math]. What is Young's modulus for wood?
First we lay out the equation for the problem:
[math]\displaystyle{ Y = \frac{stress}{strain} }[/math]
We then plug in using the numbers given to us.
[math]\displaystyle{ Y = \frac{800}{8*10^-7} }[/math]
and so Y = 10^9 N/m^2
Example 2.
The Young's Modulus of Collagen in Bone is about 6 GPa [1]. Given this, determine the force applied to a cylindrical segment of collagen of radius 1 cm and length 0.75 m to cause it to deform (stretch) 1 mm.
First, consider the equation of Young's modulus most useful for this problem:
[math]\displaystyle{ {Y = \frac{stress}{strain}} = \frac{\frac{{F}_{T}}{A}}{\frac{{ΔL}}{L_o}} }[/math]
Substitute the appropriate values:
[math]\displaystyle{ 6000000000 = \frac{\frac{{F}_{T}}{3.14*0.01^2}}{\frac{{0.001}}{0.75}} }[/math]
Solve for F:
[math]\displaystyle{ {F = 2.55*10^{10} Newtons} }[/math]
Does this seem reasonable? Yes! Collagen that makes up bone is a very hard material and does not stretch easily. Making bone stretch 1 mm longitudinally (using the bone as a vertical spring system) will take a lot of force.
Middling
Example 1.
A flan created by Dr. Schatz has a strawberry placed on it, stretching the flan from a length of 0.15 m to 0.2 m. The flan has a cross sectional area of .01. With the knowledge that flan has a Young’s modulus of ~ 1.6e4 in tension, what force was used to stretch the flan?
First we would write out the equation for Youngs modulus: [math]\displaystyle{ {Y = \frac{stress}{strain}} = \frac{\frac{{F}_{T}}{A}}{\frac{{ΔL}}{L_o}} }[/math]
Next we would fill in the equation for Young's Modulus: [math]\displaystyle{ {1.6e4 = \frac{\frac{{F}_{T}}{.01}}{\frac{{.05}}{.15}}} }[/math]
We can then fill in every thing that we know: [math]\displaystyle{ {16000 = 300*F_T} }[/math]
And so,[math]\displaystyle{ {F_T} }[/math] is equal to 53.3!
Example 2.
A man of weight 100 kg gets onto a bungee jump ride at a carnival. He is suspended in air by one rubber band (Young's Modulus of 0.01 GPa [2] of diameter 5 cm and original length of 10 m. Calculate the stretch of the band when the man reaches the bottom of the ride.
First, use the appropriate Young's Modulus equation:
[math]\displaystyle{ Y = \frac{\frac{{F}_{T}}{A}}{\frac{{ΔL}}{L_o}} }[/math]
Then, substitute the appropriate values:
[math]\displaystyle{ {1e7 = \frac{{\frac{100*9.8}{3.14*0.05^2}}}{{\frac{ΔL}{10}}}} }[/math]
Solve:
[math]\displaystyle{ {ΔL=.125 m} }[/math]
Difficult
Example 1.
A new cylandrical flan is created by Dr. Schatz which has an orange placed on it which has a mass of .15 kg, compressing the flan a certain amount. Knowing that the initial length of the flan was .15 m and the flan has a diameter of .2 meters. With the knowledge that flan has a Young’s modulus of ~ 2e5 in tension, what length is the flan now?
First we need to write down the equation:
First we would write out the equation for Youngs modulus: [math]\displaystyle{ {Y = \frac{stress}{strain}} = \frac{\frac{{F}_{T}}{A}}{\frac{{ΔL}}{L_o}} }[/math]
Next, let's solve for the unknowns: Cross sectional area:
[math]\displaystyle{ {A} = pi*r^2 }[/math] [math]\displaystyle{ {A} = pi*.1^2 }[/math] [math]\displaystyle{ {A} = .0314 meters^2 }[/math]
Force of the orange:
[math]\displaystyle{ {F}_{T} = m*g }[/math] [math]\displaystyle{ {F}_{T} = .15*-9.8 }[/math] [math]\displaystyle{ {F}_{T} = -1.47 Newtons }[/math]
Next we would write out the equation for Youngs modulus: [math]\displaystyle{ {2e5 = \frac{\frac{-1.47}{.0314}}{\frac{{ΔL}}{.15}}} }[/math]
We can solve the equation for : [math]\displaystyle{ {-7/ΔL = 200000} }[/math]
And so,[math]\displaystyle{ {ΔL } }[/math] is equal to -3.5e-5! It was compressed 3.5e-5 meters!
Example 2.
Using the Young's modulus of Tungsten ([math]\displaystyle{ 4*10^11 }[/math][3]) determine the interatomic "spring" stiffness of Tungsten.
First, find the center-to-center distance between 2 tungsten atoms.
[math]\displaystyle{ \frac{\frac{184 grams/mole}{6.022*10^23 atoms/mol}}{d^3}=19.25 g/cm^3 }[/math] where d is the interatomic distance between Tungsten atoms. (19.25 g/cm^3 is the density of Tungsten[4]).
Solving, we get:
[math]\displaystyle{ d = 2.51e-8 }[/math]
Using the appropriate formula:
[math]\displaystyle{ {Y = \frac{Ksi}{d}} }[/math]
[math]\displaystyle{ {4*10^11 = \frac{Ksi}{2.51e-8}} }[/math]
[math]\displaystyle{ {Ksi = 10040 N/m} }[/math]
Connectedness
- 1. How is this topic connected to something that you are interested in?
I am interested in engineering, and Young’s Modulus is directly relevant to this field. Young’s Modulus is used to calculate the stiffness of materials, which is useful in structural engineering applications. In high school, I partook in scientific competitions and had to construct certain structures with a partner in a time limit. The stiffness of different materials available determined whether or not they would adequately hold up other parts of the structure and allow the entire structure to remain intact. Therefore, the Young’s Modulus was directly relevant to my interests.
- 2. How is it connected to your major?
I am majoring in Computer Science. If I worked for an architectural firm, I could write code to calculate the Young’s Modulus of different building materials that the firm wanted to use to construct its buildings. The code could also determine whether or not the material was safe to use for a specific building design based on the value of the Young’s Modulus.
- 3. Is there an interesting industrial application?
- a. Engineers and architects use the Young’s Modulus to determine whether or not the material that they are using to construct a particular structure can withstand a certain amount of force (based on the structure they are building, i.e. a bridge vs. a skyscraper).
- b. Scientists (including physicists) use Young’s Modulus to see how strong the materials that they plan to use in experiments are. (This is especially important in experiments in which a lot of pressure or force is applied to the material in question.)
- c. Doctors and scientists, such as biomedical engineers, need to use Young’s Modulus to determine whether certain materials are appropriate to use to construct prosthetics for people (i.e. how rigid or flexible the materials will be).
- Young's modulus is connected to all solid material, and it highlights the slight impression given to everything showing that things do push down ever so slightly on stuff that seems stationary.
- Young's modulus is used all the time in civil engineering and it is often used to help determine structural integrity of certain materials when deciding on a building.
- Young's modulus has several biomedical applications in prosthetics and in human disease. It is used to determine the structural characteristics of prosthetic material used for implants. Young's modulus of tissues changes with aging and is being studied as a factor to evaluate mortality related to vascular stiffness from aging.
History
Young's Modulus was first developed in 1727 by the famous Leonhard Euler in Switzerland, but it was further expanded upon by Italian scientist Giordano Riccati in 1782. Finally, it was given a name by the British Scientist Thomas Young who finished work on it in the 1800s. It is used in order to discover the elasticity of solid materials and shows the stress per strain of a solid material.
Young’s Modulus is named for Thomas Young (1773-1829), an Englishman who worked as a medical practitioner. Young conducted a great deal of research on the workings of the human eye, writing papers such as “The Mechanism of the Eye” and “On the Theory of Light and Colors,” which laid the foundations for what we now know about how the eye works and processes light that it receives from its surroundings. He also translated a solid portion of the demotic script of the Rosetta Stone and found a connection between the script and Egyptian hieroglyphics. He later created a dictionary filled with hieroglyphic vocabulary.
He made his famous discovery of the Young’s Modulus while working as a lecturer at the Royal Institution. He explained that the stiffness of any elasticity could be expressed as a modulus of its elasticity. He correctly calculated the stress distribution upon a bar, leading to the discovery of the Young’s Modulus formula (which is “stress” divided by “strain”). His newly discovered equation did have practical applications, as London engineers (i.e. one company was Chapman and Buhagiar) used it to construct steel columns and other building designs.
See also
Further reading
The VERY in-depth wiki page which goes for beyond applications in physics 1.[5]
That resource is especially useful if you are pursuing a degree in Materials Science and Engineering (MSE) or any other related fields.
External links
HyperPhysics[6], which is a great tool for just about any entry-level physics curriculum.
References
Image: [7]
History: [8]