Young's Modulus

This page discusses Young's Modulus and examples of how it is used.

Claimed by Jlafiandra6

The Main Idea

Young's Modulus is a macroscopic property of a material that measures how stretchy a solid material is. It is independent of size or weight, and it will change depending on the material.

A Mathematical Model

The definition of Young's Modulus can be expressed as: [math]\displaystyle{ {Y = \frac{stress}{strain}} = \frac{\frac{{F}_{T}}{A}}{\frac{{ΔL}}{L_o}} }[/math] where [math]\displaystyle{ {F}_{T} }[/math] is equal to the tension force, [math]\displaystyle{ A }[/math] is equal to the cross sectional area, [math]\displaystyle{ ΔL }[/math] is equal to the change in length due to the tension force, and [math]\displaystyle{ L_o }[/math] is equal to the initial length of the material.

A Computational Model

It's hard to demonstrate Young's Modulus through programming, but this photo does a great job of demonstrating the concept. A force causes a solid material to stretch by a constant certain amount. This relationship is named Young's Modulus and is independent of mass of the object, and varies based on material.

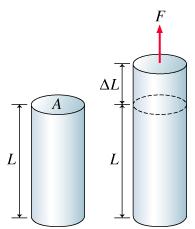
Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

A cylinder of wood has a stress of 800 and a strain of [math]\displaystyle{ 8*10^-7 }[/math]. What is Young's modulus for wood?

First we lay out the equation for the problem:

[math]\displaystyle{ {Y = \frac{stress}{strain}} }[/math]

We then plug in using the numbers given to us.

[math]\displaystyle{ {Y = \frac{800}{8*10^-7}} }[/math]

and so Y = 10^9 N/m^2

Middling

A flan created by Dr. Schatz has a strawberry placed on it, stretching the flan from a length of 0.15 m to 0.2 m. The flan has a cross sectional area of .01. With the knowledge that flan has a Young’s modulus of ~ 1.6e4 in tension, what force was used to stretch the flan?

First we would write out the equation for Youngs modulus: [math]\displaystyle{ {Y = \frac{stress}{strain}} = \frac{\frac{{F}_{T}}{A}}{\frac{{ΔL}}{L_o}} }[/math]

Next we would fill in the equation for Young's Modulus: [math]\displaystyle{ {1.6e4 = \frac{\frac{{F}_{T}}{.01}}{\frac{{.05}}{.15}}} }[/math]

We can then fill in every thing that we know: [math]\displaystyle{ {16000 = 300*F_T} }[/math]

And so,[math]\displaystyle{ {F_T} }[/math] is equal to 53.3!

Difficult

A new cylandrical flan is created by Dr. Schatz which has an orange placed on it which has a mass of .15 kg, compressing the flan a certain amount. Knowing that the initial length of the flan was .15 m and the flan has a diameter of .2 meters. With the knowledge that flan has a Young’s modulus of ~ 2e5 in tension, what length is the flan now?

First we need to write down the equation:

First we would write out the equation for Youngs modulus: [math]\displaystyle{ {Y = \frac{stress}{strain}} = \frac{\frac{{F}_{T}}{A}}{\frac{{ΔL}}{L_o}} }[/math]

Next, let's solve for the unknowns: Cross sectional area:

[math]\displaystyle{ {A} = pi*r^2 }[/math] [math]\displaystyle{ {A} = pi*.1^2 }[/math] [math]\displaystyle{ {A} = .0314 meters^2 }[/math]

Force of the orange:

[math]\displaystyle{ {F}_{T} = m*g }[/math] [math]\displaystyle{ {F}_{T} = .15*-9.8 }[/math] [math]\displaystyle{ {F}_{T} = -1.47 Newtons }[/math]

Next we would write out the equation for Youngs modulus: [math]\displaystyle{ {2e5 = \frac{\frac{-1.47}{.0314}}{\frac{{ΔL}}{.15}}} }[/math]

We can solve the equation for : [math]\displaystyle{ {-7/ΔL = 200000} }[/math]

And so,[math]\displaystyle{ {ΔL } }[/math] is equal to -3.5e-5! It was compressed 3.5e-5 meters!

Connectedness

1. Young's modulus is connected to all solid material, and it highlights the slight impression given to everything showing that things do push down ever so slightly on stuff that seems stationary.
2. My major is CS, so not a ton in physics directly applies to it, but Young's modulus is guaranteed to be in every physics simulation built which attempts to simulate the building integrity and usage of materials.
3. Young's modulus is used all the time in civil engineering and it is often used to help determine structural integrity of certain materials when deciding on a building.

History

Young's Modulus was first developed in 1727 by the famous Leonhard Euler in Switzerland, but it was further expanded upon by Italian scientist Giordano Riccati in 1782. Finally, it was given a name by the British Scientist Thomas Young who finished work on it in the 1800s. It is used in order to discover the elasticity of solid materials and shows the stress per strain of a solid material.

See also

Leonhard Euler

Thomas Young

Further reading

The VERY in-depth wiki page which goes for beyond applications in physics 1.[1]

External links

HyperPhysics[2] which is a great tool for just about any entry level physics.

References

Image: [3]

History: [4]