Translational, Rotational and Vibrational Energy

Main Idea

In many cases, analyzing the kinetic energy of an object is in fact more difficult than just applying the formula [math]\displaystyle{ K = \cfrac{1}{2}mv^2 }[/math]. When you throw a ball, for example, the ball is traveling through the air, but will also rotate around its own axis. When analyzing more complicated movements like this one, it is necessary to break kinetic energy into different parts and analyze each one separately.

The kinetic energy associated to the movement of the center of mass of the object is called the translational kinetic energy. In terms of the example above, this would be the kinetic energy of the movement of the center of mass of the ball through the air.

The kinetic energy associated to the rotation or vibration of the atoms of the object around its center or axis is called the relative kinetic energy. This kinetic energy is the energy of the ball rotating on its own axis. If this is difficult to visualize, think about how an american football rotates about its center axis when you throw it correctly.

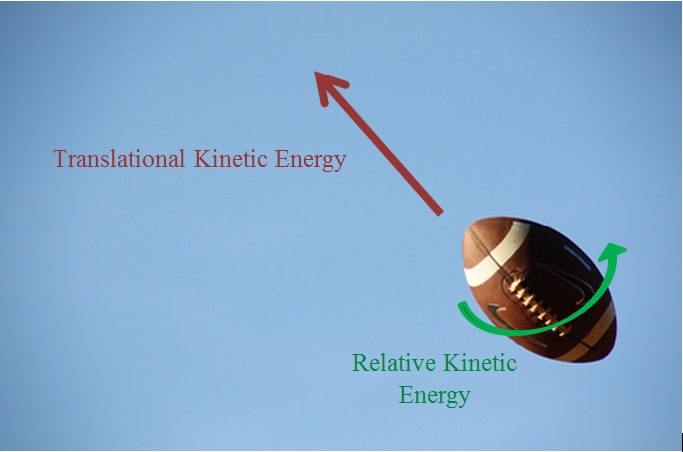
A Mathematical Model

Total Kinetic Energy

As we just saw, kinetic energy can be divided into two energies: translational kinetic energy and rotational kinetic energy. Therefore, the total kinetic energy of a system is equal to the sum of those two kinetic energies:

[math]\displaystyle{ K_{total} = K_{translational} + K_{relative} }[/math]

The relative kinetic energy term can itself be divided into two other terms. The energy of the atoms of the object relative to its center or axis can either be rotational (this is the case of the football thrown in the air) or vibrational. Therefore, we have:

[math]\displaystyle{ K_{total} = K_{translational} + K_{relative} = K_{translational} + K_{rotational} + K_{vibrational} }[/math]

Calculating Translational Kinetic Energy

Because the translational kinetic energy is associated to the movement of the center of mass of the object, it is important to know how to calculate the location of the center of mass.

[math]\displaystyle{ r_{CM} = \cfrac{m_1r_1 + m_2r_2+m_3r_3 + ...}{Mass} }[/math]

The velocity of the center of mass is given by the equation:

[math]\displaystyle{ v_{CM} = \cfrac{m_1v_1 + m_2v_2+m_3v_3 + ...}{Mass} }[/math]

Using the total mass and the velocity of the center of mass, we can thus calculate the translational energy of an object:

[math]\displaystyle{ K_{translational} = \cfrac{1}{2}M_{total}v_{CM}^2 }[/math]

Calculating Rotational Kinetic Energy

Similarly, we can calculate rotational kinetic energy with the following formula:

[math]\displaystyle{ K_{rotational} = \cfrac{1}{2}M_{total}v{CM}^2 }[/math]

Moment of Inertia

But rotational kinetic energy can also be calculated with the moment of inertia and the angular speed of an object. The moment of inertia of an object is the sum of the products of the mass of each particle in the object with the square of their distance from the axis of rotation. The general formula for calculating the moment of inertia of an object is:

[math]\displaystyle{ I = m_1r_{\perp,1}^2 + m_2r_2{\perp,2}^2 + m_3r_{\perp,3}^2 +... }[/math] [math]\displaystyle{ kg.m^2 }[/math]

Some examples of moments of inertia:

For a ring, the moment of inertia formula leads to [math]\displaystyle{ I = MR^2 }[/math] because all of the atoms in the ring are at equal distance from the center.

For a long thin rod, we get [math]\displaystyle{ I = \cfrac{1}{12}ML^2 }[/math], where L is the length of the rod.

For a cylinder of length L and radius R, the formula leads us to [math]\displaystyle{ \cfrac{1}{12}ML^2 + \cfrac{1}{4}MR^2 }[/math]

For a disk, [math]\displaystyle{ I = \cfrac{1}{2}MR^2 }[/math]

For a sphere , [math]\displaystyle{ I = \cfrac{2}{5}MR^2 }[/math]

Angular Speed

The angular speed is a calculation of how fast the object is rotating. It can be calculated from the period, T, with the following formula : [math]\displaystyle{ \omega = \cfrac{2\pi}{T} }[/math]

The rotational kinetic energy can thus be calculated using these two variables: [math]\displaystyle{ K_{rotational} = \cfrac{1}{2}I\omega^2 }[/math].

Point Particle System VS Extended System

Why is it useful to divide the kinetic energy into two different elements? When calculating the total energy of a system, depending on how it is modeled, it will contain one or more types of kinetic energies. Let's think about a system modeled as a point particle system. In this model of a system, we think of the object as one point, located at its center of mass. With this way of thinking, it becomes clear that there can only be one type of kinetic energy: translational kinetic energy. There cannot be any rotational kinetic energy because there are no atoms rotating about the center of mass, since we are thinking of the center of mass as the entire object. Our general energy equation thus boils down to this:

[math]\displaystyle{ \triangle E_{system} = W }[/math] where [math]\displaystyle{ W = F_{net} . \triangle r_{CM} }[/math] and [math]\displaystyle{ \triangle E_{system} = \triangle K_{translational} }[/math] since there is only translational kinetic energy.

We end up with [math]\displaystyle{ \triangle K_{translational} = F_{net} . \triangle r_{CM} }[/math]

Note: There may also be spring potential energy and rest energy depending on the example.

Therefore, viewing a system as a point particle system allows us to easily calculate the translational kinetic energy. This translational kinetic energy will be the same in the extended system.

After having calculated the translational kinetic energy of the system using the point particle system, we can use this value to calculate other terms in the general equation in the extended system.

We start with the general energy equation: [math]\displaystyle{ \triangle E_{system} = W }[/math] where [math]\displaystyle{ W = F_{net} . displacement }[/math]

In this extended system, we consider all the atoms and their rotation about the axis as well as the general movement of the center of mass. We end up with [math]\displaystyle{ \triangle K_{translational} + \triangle K_{rotational} + \triangle K_{vibrational} = F_{net} . displacement }[/math]

Note: Here again, there may be spring potential energy and rest energy included in this equation depending on the example.

A Computational Model

How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

Problem statement:

Calculate the rotational kinetic energy of a wheel of radius 100cm, mass 10kg, with and angular velocity of 22 radians/s.

Solution:

We know how to calculate the moment of inertia for a disk, and the moment of inertia for a wheel will be the same since all the atoms are at the same distance from the center. Therefore, [math]\displaystyle{ I = MR^2 = (10)(1)^2 = 10 kgm^2 }[/math]

From there, we can easily calculate the rotational kinetic energy: [math]\displaystyle{ K_{rotational} = \cfrac{1}{2}I\omega^2 = \cfrac{1}{2}(10)(22)^2 = 2420 }[/math] Joules

Middling

Difficult

Connectedness

How is this topic connected to something that you are interested in?

In the book, this topic is very much related to sports. It uses countless examples from diving, ice skating or frisbee to demonstrate why kinetic energy can be separated into two terms. I have always been interested in sports and they were always a big part of my life. Therefore when I read the book, this was one of the most interesting sections to me because I felt some kind of connection to it, like it applied to my life, since I had ice-skated and dove when I was young.

How is it connected to your major?

Some biomedical engineers go on to work with sports stars on smart clothes or even prosthetics, in which case they have to deal with rotation and vibration, in addition to regular kinetic energy.

Is there an interesting industrial application?

When designing a ball for example, one needs to think about design choices that enable it to be thrown far.

History

Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.