Translational, Rotational and Vibrational Energy: Difference between revisions
Epourchet3 (talk | contribs) No edit summary |
Epourchet3 (talk | contribs) No edit summary |
||
| Line 44: | Line 44: | ||
'''Some examples of moments of inertia:''' | '''Some examples of moments of inertia:''' | ||
For a ring, the moment of inertia formula leads to <math> I = MR^2 </math> because all of the atoms in the ring are at equal distance from the center. | For a ring, the moment of inertia formula leads to <math> I = MR^2 </math> because all of the atoms in the ring are at equal distance from the center. | ||
For a long thin rod, we get <math> I = \cfrac{1}{12}ML^2 </math>, where L is the length of the rod. | For a long thin rod, we get <math> I = \cfrac{1}{12}ML^2 </math>, where L is the length of the rod. | ||
For a cylinder of length L and radius R, the formula leads us to <math> \cfrac{1}{12}ML^2 + \cfrac{1}{4}MR^2 </math> | |||
For a disk, <math> I = \cfrac{1}{2}MR^2 </math> | |||
For a sphere , <math> I = \cfrac{2}{5}MR^2 </math> | |||
===A Computational Model=== | ===A Computational Model=== | ||
Revision as of 17:02, 27 November 2015
Main Idea
In many cases, analyzing the kinetic energy of an object is in fact more difficult than just applying the formula [math]\displaystyle{ K = \cfrac{1}{2}mv^2 }[/math]. When you throw a ball, for example, the ball is traveling through the air, but will also rotate around its own axis. When analyzing more complicated movements like this one, it is necessary to break kinetic energy into different parts and analyze each one separately.
The kinetic energy associated to the movement of the center of mass of the object is called the translational kinetic energy. In terms of the example above, this would be the kinetic energy of the movement of the center of mass of the ball through the air.
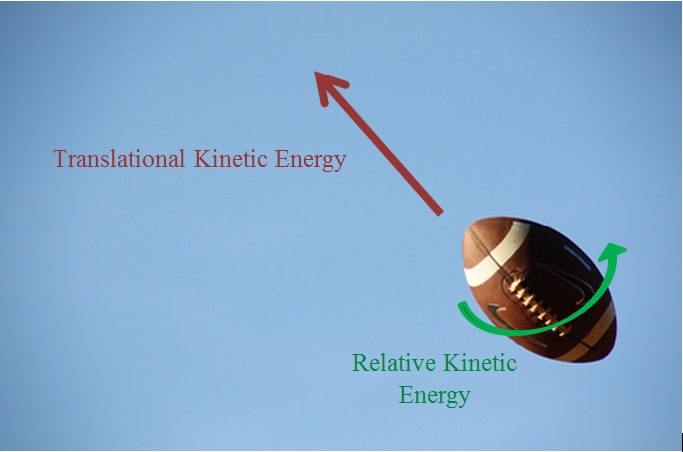
The kinetic energy associated to the rotation or vibration of the atoms of the object around its center or axis is called the relative kinetic energy. This kinetic energy is the energy of the ball rotating on its own axis. If this is difficult to visualize, think about how an american football rotates about its center axis when you throw it correctly.
A Mathematical Model
As we just saw, kinetic energy can be divided into two energies: translational kinetic energy and rotational kinetic energy. Therefore, the total kinetic energy of a system is equal to the sum of those two kinetic energies:
[math]\displaystyle{ K_{total} = K_{translational} + K_{relative} }[/math]
The relative kinetic energy term can itself be divided into two other terms. The energy of the atoms of the object relative to its center or axis can either be rotational (this is the case of the football thrown in the air) or vibrational. Therefore, we have:
[math]\displaystyle{ K_{total} = K_{translational} + K_{relative} = K_{translational} + K_{rotational} + K_{vibrational} }[/math]
Because the translational kinetic energy is associated to the movement of the center of mass of the object, it is important to know how to calculate the location of the center of mass.
[math]\displaystyle{ r_{CM} = \cfrac{m_1r_1 + m_2r_2+m_3r_3 + ...}{Mass} }[/math]
The velocity of the center of mass is given by the equation:
[math]\displaystyle{ v_{CM} = \cfrac{m_1v_1 + m_2v_2+m_3v_3 + ...}{Mass} }[/math]
Using the total mass and the velocity of the center of mass, we can thus calculate the translational energy of an object:
[math]\displaystyle{ K_{translational} = \cfrac{1}{2}M_{total}v_{CM}^2 }[/math]
Similarly, we can calculate rotational kinetic energy with the following formula:
[math]\displaystyle{ K_{rotational} = \cfrac{1}{2}M_{total}v{CM}^2 }[/math]
But rotational kinetic energy can also be calculated with the moment of inertia and the angular momentum of an object. The moment of inertia of an object is the sum of the products of the mass of each particle in the object with the square of their distance from the axis of rotation. The general formula for calculating the moment of inertia of an object is:
[math]\displaystyle{ I = m_1r_{\perp,1}^2 + m_2r_2{\perp,2}^2 + m_3r_{\perp,3}^2 +... }[/math] [math]\displaystyle{ kg.m^2 }[/math]
Some examples of moments of inertia:
For a ring, the moment of inertia formula leads to [math]\displaystyle{ I = MR^2 }[/math] because all of the atoms in the ring are at equal distance from the center. For a long thin rod, we get [math]\displaystyle{ I = \cfrac{1}{12}ML^2 }[/math], where L is the length of the rod. For a cylinder of length L and radius R, the formula leads us to [math]\displaystyle{ \cfrac{1}{12}ML^2 + \cfrac{1}{4}MR^2 }[/math] For a disk, [math]\displaystyle{ I = \cfrac{1}{2}MR^2 }[/math] For a sphere , [math]\displaystyle{ I = \cfrac{2}{5}MR^2 }[/math]
A Computational Model
How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript
Examples
Be sure to show all steps in your solution and include diagrams whenever possible
Simple
Middling
Difficult
Connectedness
- How is this topic connected to something that you are interested in?
- How is it connected to your major?
- Is there an interesting industrial application?
History
Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
See also
Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
Further reading
Books, Articles or other print media on this topic
External links
Internet resources on this topic
References
This section contains the the references you used while writing this page