Torque vs Work: Difference between revisions
| Line 213: | Line 213: | ||
[http://physics.stackexchange.com/ Physics Stack Exchange]<div></div> | [http://physics.stackexchange.com/ Physics Stack Exchange]<div></div> | ||
[https://en.wikipedia.org/wiki/Torque Wikipedia Torque]<div></div> | [https://en.wikipedia.org/wiki/Torque Wikipedia Torque]<div></div> | ||
[[Category: Angular Momentum]] | [[Category: Angular Momentum]] | ||
Latest revision as of 12:33, 25 July 2019

When it comes to our universe, there still remains much that we do not understand. That we we do know and understand, we measure in relation to other ideas or subjects, in terms of abstracts we call units. In modern physics, and most mathematical applications we relate and measure matter and interactions in terms of these units. However, two such descriptions having the same units does necessarily connotate a representation of the same idea or measurement. Here, we will examine one such occurrence in modern physics, specifically the difference between torque and work when both are expressed as Newton*meters.
The Newton-Meter --> Vector vs Scaler
In modern physics, there a two concepts that, while describing different ideas, happen to utilize the same units, these units being:
[math]\displaystyle{ Newton * meters }[/math] [math]\displaystyle{ (N * m) }[/math]
Mathematical Model: The Concepts
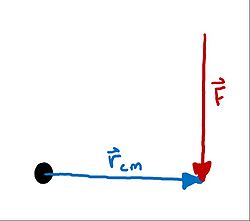
The first of these concepts is torque, which is a measurement of the moment that a force causes in a system. A moment is also known as a system's tendency of a force to cause rotation.
[math]\displaystyle{ \vec{\tau} = \vec{r_{cm}} \times \vec{F} }[/math]
Torque can also be represented through rotational kinematics, whereby the rotational acceleration and the moment of inertia are multiplied together to equal torque: [math]\displaystyle{ \vec{\tau} = \vec{I} \cdot \vec{\alpha} }[/math]
where [math]\displaystyle{ \tau }[/math] is the vector cross product of the force vector and position vector relative to the center of mass
The second concept is work, which is the measurement of a force acting over a distance on a given system.
[math]\displaystyle{ W = \vec{F} \cdot \vec{r} }[/math]
where W is the scalar dot product of the force vector and change in position vector
Both of these concepts are measured using the units of [math]\displaystyle{ Newton * meters }[/math] , however torque is a vector value while work is a scalar value. This is a key point to keep in mind.
Previously, in Physics, when we addressed the energy principle and energy in general, we describe the measurement of energy and change in energy using the units:
[math]\displaystyle{ Joules }[/math] [math]\displaystyle{ (J) }[/math]
As it happens, work on a system is also equivalent to the change in kinetic energy of a system and therefore can also be expressed in joules. Positive work will add kinetic energy to a system whereas negative work will subtract kinetic energy from a system.
[math]\displaystyle{ W = \Delta K = K_{final} - K_{initial} }[/math]
where W is the work done and K is the kinetic energy of the system.
So, work can be expressed in terms of joules, which means that torque can be expressed in terms of joules too, right? Well, it's not quite as straightforward as changing units. Remember, work is a scalar measurement, while torque is a vector representation. The two quantities must be measured individually because while work effects the linear momentum of a system, torque effects the angular momentum of a system. To put it in common terms, work relates to the movement of a system from one position to another while torque relates to the twisting of the system itself. So in fact, they represent very different concepts.
Nuances in Work
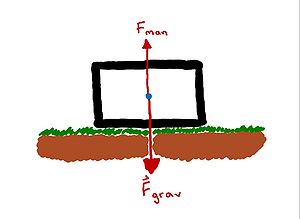
According to it's definition, work is a force acting over a given distance. So what about forces acting on an object that does not move? Let's look at an example. Take this block sitting on the earth and being acted on by a man who tries to lift it.
Let the mass of the block be [math]\displaystyle{ 5 kg }[/math] and the force of the man pulling up be [math]\displaystyle{ 20 N }[/math].
We know: [math]\displaystyle{ F = mg }[/math] where F is the force of gravity, m is the mass of the object, and g is the acceleration due to gravity
Force due to man: [math]\displaystyle{ F_{man} = 20 N }[/math]
Force due to gravity: [math]\displaystyle{ F_{grav} = (5 kg) * (-9.8 m/(s^{2}) = -49 N }[/math]
Net force: [math]\displaystyle{ F_{net} = 20 N + (-49 N) = -29 N }[/math]
However, we know that the block will not move through the earth due to the force of the earth acting on it, and so the block will stay in place. Since the block does not move there is no change in position. Applying this to our formula for work:
Work by man: [math]\displaystyle{ W_{man} = \vec{F}_{man} * \vec{r}_{block} = \lt 0, 20, 0\gt N * \lt 0, 0, 0\gt m = (0*0)Nm + (20*0)Nm + (0*0)Nm = 0 Nm }[/math]
So even though the man applied a force to the block, no work was done because the block did not move. It a very important to realize that it doesn't matter how large the force applied to an object is, if the object does not move, no work is done.
In this situation: [math]\displaystyle{ W = ∆K = 0Nm }[/math]
Nuances in Torque
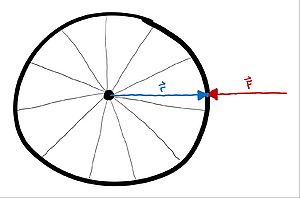
Like work, torque also has some interesting situations that are important to take note of. Consider the following example where a wheel is being acted on by a force that is directly toward the center of mass of the wheel.
Let the radius of the wheel be [math]\displaystyle{ 2 m }[/math] and the force applied be [math]\displaystyle{ 15 N }[/math].
Using these values, let's take the cross product of position cross force to find the torque cause by the force on the wheel.
Torque: [math]\displaystyle{ \vec{\tau} = \vec{r}_{cm} \times \vec{F} = \lt 2, 0, 0\gt m \times \lt -15, 0, 0\gt N }[/math]
[math]\displaystyle{ \vec{\tau} = (2 m * -15 N)(iXi) + (2 m * 0 N)(iXj) + (2 m * 0 N)(iXk) + (0 m * -15 N)(jXi) + (0 m * 0 N)(jXj) + (0 m * 0 N)(jXk) + (0 m * 0 N)(kXi) + (0 m * 0 N)(kXj) + (0 m * 0 N)(kXk) }[/math]
[math]\displaystyle{ \vec{\tau} = (-30 Nm)(0) + (0 Nm)(k) + (0 Nm)(-j) + (0 Nm)(-k) + (0 Nm)(0) + (0 Nm)(i) + (0 Nm)(j) + (0 Nm)(-i) + (0 Nm)(0) }[/math]
[math]\displaystyle{ \vec{\tau} = \lt 0, 0, 0\gt Nm }[/math]
So, even though a force was applied at a distance relative to the center of mass of the wheel, there was no net torque because the force was acting straight through the center of mass of the wheel. This is important to remember as any force acting through an objects center of mass may be disregarded as having any effect on the torque and therefore does not change the angular momentum of the object.
Example Problems
Simple Torque
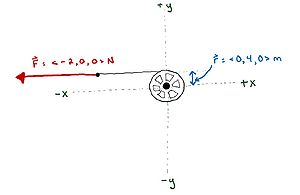
If the center of mass of the spool of thread is at the origin, determine the torque caused by the force as shown below.
Solution:
[math]\displaystyle{ \vec{\tau} = \vec{r}_{cm} \times \vec{F} }[/math]
[math]\displaystyle{ \vec{\tau} = \lt 0, 4, 0\gt m \times \lt -2, 0, 0\gt N }[/math]
[math]\displaystyle{ \vec{\tau} = (0 m * -2 N)(iXi) + (0 m * 0 N)(iXj) + (0 m * 0 N)(iXk) + (4 m * -2 N)(jXi) + (4 m * 0 N)(jXj) + (4 m * 0 N)(jXk) + (0 m * -2 N)(kXi) + (0 m * 0 N)(kXj) + (0 m * 0 N)(kXk) }[/math]
[math]\displaystyle{ \vec{\tau} = (0 Nm)(0) + (0 Nm)(k) + (0 Nm)(-j) + (-8 Nm)(-k) + (0 Nm)(0) + (0 Nm)(i) + (0 Nm)(j) + (0 Nm)(-i) + (0 Nm)(0) }[/math]
[math]\displaystyle{ \vec{\tau} = \lt 0, 0, 8\gt N*m }[/math]
Middling Work
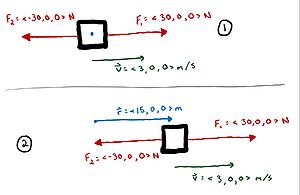
In the system below, determine the net work that is accomplished by the two forces:
Solution:
[math]\displaystyle{ W = \vec{F} \cdot \vec{r} }[/math]
[math]\displaystyle{ W_{1} = \lt 30, 0, 0\gt N \cdot \lt 15, 0, 0\gt m }[/math]
[math]\displaystyle{ W_{1} = (30 N)(15 m) + (0 N)(0 m) + (0 N)(0 m) }[/math]
[math]\displaystyle{ W_{1} = 450 Nm + 0 Nm + 0 Nm }[/math]
[math]\displaystyle{ W_{1} = 450 Nm }[/math]
[math]\displaystyle{ W_{2} = \lt -30, 0, 0\gt N \cdot \lt 15, 0, 0\gt m }[/math]
[math]\displaystyle{ W_{2} = (-30 N)(15 m) + (0 N)(0 m) + (0 N)(0 m) }[/math]
[math]\displaystyle{ W_{2} = -450 Nm + 0 Nm + 0 Nm }[/math]
[math]\displaystyle{ W_{2} = -450 Nm }[/math]
[math]\displaystyle{ W_{net} = W_{1} + W_{2} }[/math]
[math]\displaystyle{ W_{net} = 450 Nm - 450 Nm }[/math]
[math]\displaystyle{ W_{net} = 0 N \cdot m }[/math]
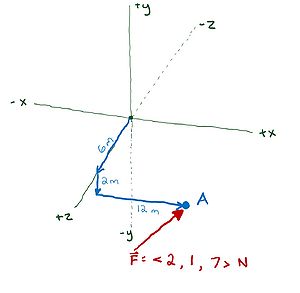
Difficult Torque
In the complex system below, determine the given force is applied at point A. Determine the net torque about the origin due to the force.
Solution:
[math]\displaystyle{ \vec{r} = \lt 12, -2, 6\gt m }[/math]
[math]\displaystyle{ \vec{\tau} = \vec{r}_{cm} \times \vec{F} }[/math]
[math]\displaystyle{ \vec{\tau} = \lt 12, -2, 6\gt m \times \lt 2, 1, 7\gt N }[/math]
[math]\displaystyle{ \vec{\tau} = (12 m * 2 N)(iXi) + (12 m * 1 N)(iXj) + (12 m * 7 N)(iXk) + (-2 m * 2 N)(jXi) + (-2 m * 1 N)(jXj) + (-2 m * 7 N)(jXk) + (6 m * 2 N)(kXi) + (6 m * 1 N)(kXj) + (6 m * 7 N)(kXk) }[/math]
[math]\displaystyle{ \vec{\tau} = (24 Nm)(0) + (12 Nm)(k) + (84 Nm)(-j) + (-4 Nm)(-k) + (-2 Nm)(0) + (-14 Nm)(i) + (12 Nm)(j) + (6 Nm)(-i) + (42 Nm)(0) }[/math]
[math]\displaystyle{ \vec{\tau} = \lt -20, -72, 16\gt N \cdot m }[/math]
For these types of problems, it is best to split the problem into smaller pieces, identify the lever arms where torques are applied, and work your way back up.
Connectedness
Connected to My Own Interests?
While I am more interested in digital and electronic designs, I love to tinker and create with mechanical devices. In order to make a device efficient and able to function without breaking, you must understand how work is done and the strain that torque can put on a device.
Connected to Electrical Engineering?
While torque and work are not integral parts of electrical engineering, it is very important to understand the two concepts because they do have the potential to alter the design of something I might construct. In this day and age, everything is electronic and most modern tools even use digital instructions. It's important when designing a mechanical tool to understand torque in order to determine the best avenue through which to run wire and to know how much extra give to allow to wire to move if the tools workload necessitates movement.
Connected to Industry
The industrial applications for both torque and work are enormous. From power tools, to vehicles, to simple machines. If one can do more wore with less energy, or apply greater torque with smaller forces, it greatly increases the workload that an individual can accomplish. So, yes, torque and work are quite important in industry.
Origin
Torque
The idea of torque first originated with Aristotle and his work with levers.
Work
Energy was also initially a notion put forth by Aristotle, but the concept of work was something later derived by several scientists and mathematicians, including Joule and Carnot.