Potential Difference in a Uniform Field: Difference between revisions

From Physics Book
Jump to navigation Jump to search
 
(36 intermediate revisions by 2 users not shown)
Line 1: Line 1:
By: dachtani3
By: dachtani3


'''CLAIMED BY SHAN SUEN (FALL 2016)'''
Claimed by SeongEun Park April, 2017
 


Electric potential is a scalar quantity that is used to describe the change in electric potential energy per unit charge. This page will elaborate on the change in electric potential in a uniform field.  
Electric potential is a scalar quantity that is used to describe the change in electric potential energy per unit charge. This page will elaborate on the change in electric potential in a uniform field.  
Line 7: Line 9:
==The Main Idea==
==The Main Idea==


Potential difference is the change in electric potential between a final and initial location when work is done on a charge to to affect its potential energy. The unit for electric potential is a volt (which is also joule/coulomb).
Potential difference is the change in electric potential between a final and initial location when work is done on a charge to affect its potential energy. The unit for electric potential is a volt (which is also joule/coulomb). Approximation of uniform field is useful for simple calculation.
It is important to remember that since energy is stored in a form of electric field, there will be no potential energy for a single point charge alone; potential energy, thus the potential difference, exists only when there are pairs of interacting particles.  


===A Mathematical Model===
===A Mathematical Model===


This equation represents potential difference, where V is electric potential, U is electric potential energy, and q is unit charge.
This equation represents potential difference, where V is electric potential, U is electric potential energy, and q is unit charge.
The unit for electric potential is 'V' (volt), where it takes 1 Joules of work to move 1 Coulomb of unit charge per 1 volt.
:<math>\Delta V</math> = <math>\frac{dU}{q} </math>  
:<math>\Delta V</math> = <math>\frac{dU}{q} </math>  


You can rearrange this equation to also show that electric potential energy is electric potential times unit charge.  
You can rearrange this equation to also show that electric potential energy is electric potential times unit charge.  
:Hence, <math>\Delta U</math> = <math>q \Delta V</math>  
:<math>\Delta U</math> = <math>q \Delta V</math>  
 


In addition, you can express electric potential as the sum of the dot product of electric field and displacement in each dimension. This expression is as follows:
In addition, you can express electric potential as the sum of the dot product of electric field and displacement in each dimension. This expression is as follows:
:<math>\Delta V</math> = -<math>\vec{E}</math>●<math>\Delta \vec{l}</math> = = -(Ex●<math>\Delta x</math> + Ey●<math>\Delta y</math> + Ez●<math>\Delta z</math>), units = Volts (V)
:<math>\Delta V</math> = -<math>\vec{E}</math>●<math>\Delta \vec{l}</math> = -(<math>E_{x}</math>●<math>\Delta x</math> + <math>E_{y}</math>●<math>\Delta y</math> + <math>E_{z}</math>●<math>\Delta z</math>)
You can also use dot product notation:
:<math>\Delta V</math> = -<math>\vec{E}</math>●<math>\Delta \vec{l}</math> = <math> (E_{x},E_{y},E_{z})●(dX, dY, dZ) </math>




Within this expression, you can also note that the units for the electric field are V/m. We originally learned that units for electric field are N/c, but V/m is also an appropriate unit.
Potential difference can be either positive or negative because each component of electric field and displacement can be positive or negative. Within this expression, you can also note that the units for the electric field are V/m. We originally learned that units for electric field are N/c, but V/m is also an appropriate unit.


===A Computational Model===
===A Computational Model===


-A good video that showcases 3D-models of the interaction of charges with electric potential and electric potential energy can be found here:
This video showcases 3D-models of the interaction of charges with electric potential and electric potential energy. This video is especially helpful if you want to learn these topics conceptually.
 
https://www.youtube.com/watch?v=-Rb9guSEeVE
https://www.youtube.com/watch?v=-Rb9guSEeVE


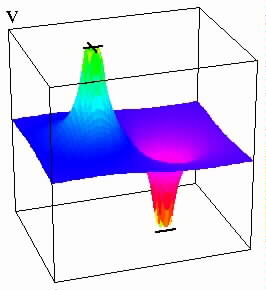
-In addition, this image showcases the relationship between electric fields and electric potential. If you take the negative gradient of electric potential, the result is the electric field. The gradient is the direction of the hills seen in the graph representing electric potential.
 
In addition, this image showcases the relationship between electric fields and electric potential. If you take the negative gradient of electric potential, the result is the electric field. The gradient is the direction of the hills seen in the graph representing electric potential.


[[File:3-d_model.jpg]]
[[File:3-d_model.jpg]]
Line 39: Line 46:
Questions 1 and 2 are based on the following situation:
Questions 1 and 2 are based on the following situation:


A path consists of two locations. Location 1 is at <.1,0,0>m and Location 2 is at <.5,0,0>m. A uniform electric field of <300,0,0> N/C exists in this region pointing from Location 1 to Location 2.  
A path consists of two locations. Location 1 is at <0.1,0,0>m and Location 2 is at <0.5,0,0>m. A uniform electric field of <300,0,0> N/C exists in this region pointing from Location 1 to Location 2.  


Question 1: What is the difference in electric potential between the two points?  
Question 1: What is the difference in electric potential between the two points?  


:dl = final location - initial location = <.5,0,0> - <.1,0,0> = <.4,0,0> m
:<math>\Delta{L}</math> = final location - initial location = <0.5, 0,0 > - <0.1, 0, 0> = <0.4, 0, 0> m
:dV = -(Exdx + Eydy + Ezdz) = -(300 N/C*.4 + 0*0 + 0*0) = -120 V
:<math>\Delta{V}</math> = -<math>\vec{E}</math>●<math>\Delta \vec{l}</math> = -(<math>E_{x}</math>●<math>\Delta x</math> + <math>E_{y}</math>●<math>\Delta y</math> + <math>E_{z}</math>●<math>\Delta z</math>)
= -(300 N/C*.4 + 0*0 + 0*0)
= -120


Answer: -120 V
Answer: -120 V
Line 56: Line 65:


===Middling===
===Middling===
figure 1:
[[File:Slide1.jpg]]


Key Point to remember about signs:
Key Point to remember about signs:


-If the path is going in the direction of the electric field, electric potential is decreasing.
1) If the path is going in the direction of the electric field, electric potential is decreasing.


:Ex: Refer to Simple Example
:Ex: Refer to Simple Example
:Ex 2: Figure 1
    - Consider the path going from point A to point B. The path is in the same direction as the electric field (red arrow).
      Because ΔV = -E●Δl = -E●Δr(A->B) = -E●d. This then refers ΔV = Vb-Va < 0, meaning that the electric potential is decreasing.


-If the path is going in the opposite direction of the electric field, electric potential is increasing.
2) If the path is going in the opposite direction of the electric field, electric potential is increasing.


:Question: Location 1 is at <.1,0,0> and Location 2 is at <.5,0,0>. The uniform electric field is <300,0,0> N/C. The charge travels from Location 2 to Location 1.
:Question: Location 1 is at <.1,0,0> and Location 2 is at <.5,0,0>. The uniform electric field is <300,0,0> N/C. The charge travels from Location 2 to Location 1.
Line 72: Line 86:
:Answer: + 120 V
:Answer: + 120 V


-If the path is perpendicular to the electric field, electric potential does not change.
:Ex 2: Figure 1
    - Refer back to the figure 1 above. If the path from point C to D was taken, it is going in the opposite direction of the electric field, which means that ΔV > 0;
      therefore, the potential is increasing.
 
3) If the path is perpendicular to the electric field, electric potential does not change.


:Question: Location 1 is at <.1,0,0> and Location 2 is at <.5,0,0>. The uniform electric field is <0,300,0> N/C. The charge travels from Location 1 to Location 2.
:Question: Location 1 is at <.1,0,0> and Location 2 is at <.5,0,0>. The uniform electric field is <0,300,0> N/C. The charge travels from Location 1 to Location 2.
Line 80: Line 98:


:Answer: 0V
:Answer: 0V
:Ex 2: Figure 1
      - Refer back to the figure 1 above. If the path is going from point B to C, or (point A to D), these points are perpendicular to the electric field. Because no work is required to move a
      a charge between them, all points that are perpendicular to same electric field share same electric potential.


===Difficult===
===Difficult===
Line 96: Line 118:
'''How is this topic connected to something that you are interested in?'''
'''How is this topic connected to something that you are interested in?'''


:Electric potential is related to something that I am interested in because of an internship I had dealing with circuit boards. Recently, I interned in the electronics systems lab at the Georgia Tech Research Institute. Our project was to build a integrated circuit board that acting as a no-parking zone sign for illegal parking areas. My particular board sensed the car, held the signal, and then transferred the electric signal to the audio board to display noise. On my board, I had many electronic components, including capacitors. During my internship, I placed the appropriate pieces on the board where deemed necessary, but I never really understood the physics of electricity behind the components. Hence, learning about electric potential now gives me a greater scope as to understand how electric charge and potential difference affects capacitors.  
:Potential difference is extremely applicable and interesting to me because I am a computer engineer and as a computer engineer, I deal with many things regarding electricity. I am particularly interested in building electric guitar pedals. In addition to the digital signal processing and programming aspect of guitar pedals, there is a lot of physics involved with how they work. Potential difference and electric potential kick in because in addition to the signals that are transmitted throughout the TRS cables, current also runs through them. Obviously, energy and charge are also very prominent in this so they are directly applied to the construction of guitar pedals.  


'''How is it connected to your major?'''
'''How is it connected to your major?'''


:I am an Industrial & Systems engineering major. My major is all about understanding high level processes in order to identify areas for improvement. In particular, we have the opportunity to take intro to Electrical & Computer Engineering courses to understand the ins and outs of computers and electricity processes. We learn the basics of electricity, including the history of electric scientists like Volta, as well as the definitions of electric potential and electric potential energy. These intro level classes give us a strong foundation for upper-level classes where processes we encounter become very mathematically complex.  
:As a computer engineer, in class and ideally in my job after college, I will be dealing with electronics and electricity in action. I am constantly dealing with breadboards, semiconductors, microprocessors, cables, etc. All of these things essentially require a basic understanding of physics topics especially related to electromagnetism.  


'''Is there an interesting industrial application?'''
'''Is there an interesting industrial application?'''
Line 138: Line 160:
This video that walks through examples on potential difference in a uniform field:  
This video that walks through examples on potential difference in a uniform field:  
:https://www.youtube.com/watch?v=mF3VAjcjvOA  
:https://www.youtube.com/watch?v=mF3VAjcjvOA  
This video further discusses electric potential and its concepts:
:https://www.youtube.com/watch?v=wT9AsY79f1k


This video on electric potential energy gives a good background on solving problems before learning specifically about electric potential:  
This video on electric potential energy gives a good background on solving problems before learning specifically about electric potential:  

Latest revision as of 16:35, 21 November 2020

By: dachtani3

Claimed by SeongEun Park April, 2017


Electric potential is a scalar quantity that is used to describe the change in electric potential energy per unit charge. This page will elaborate on the change in electric potential in a uniform field.

The Main Idea

Potential difference is the change in electric potential between a final and initial location when work is done on a charge to affect its potential energy. The unit for electric potential is a volt (which is also joule/coulomb). Approximation of uniform field is useful for simple calculation. It is important to remember that since energy is stored in a form of electric field, there will be no potential energy for a single point charge alone; potential energy, thus the potential difference, exists only when there are pairs of interacting particles.

A Mathematical Model

This equation represents potential difference, where V is electric potential, U is electric potential energy, and q is unit charge. The unit for electric potential is 'V' (volt), where it takes 1 Joules of work to move 1 Coulomb of unit charge per 1 volt.

[math]\displaystyle{ \Delta V }[/math] = [math]\displaystyle{ \frac{dU}{q} }[/math]

You can rearrange this equation to also show that electric potential energy is electric potential times unit charge.

[math]\displaystyle{ \Delta U }[/math] = [math]\displaystyle{ q \Delta V }[/math]

In addition, you can express electric potential as the sum of the dot product of electric field and displacement in each dimension. This expression is as follows:

[math]\displaystyle{ \Delta V }[/math] = -[math]\displaystyle{ \vec{E} }[/math]●[math]\displaystyle{ \Delta \vec{l} }[/math] = -([math]\displaystyle{ E_{x} }[/math]●[math]\displaystyle{ \Delta x }[/math] + [math]\displaystyle{ E_{y} }[/math]●[math]\displaystyle{ \Delta y }[/math] + [math]\displaystyle{ E_{z} }[/math]●[math]\displaystyle{ \Delta z }[/math])

You can also use dot product notation:

[math]\displaystyle{ \Delta V }[/math] = -[math]\displaystyle{ \vec{E} }[/math]●[math]\displaystyle{ \Delta \vec{l} }[/math] = [math]\displaystyle{ (E_{x},E_{y},E_{z})●(dX, dY, dZ) }[/math]


Potential difference can be either positive or negative because each component of electric field and displacement can be positive or negative. Within this expression, you can also note that the units for the electric field are V/m. We originally learned that units for electric field are N/c, but V/m is also an appropriate unit.

A Computational Model

This video showcases 3D-models of the interaction of charges with electric potential and electric potential energy. This video is especially helpful if you want to learn these topics conceptually.

https://www.youtube.com/watch?v=-Rb9guSEeVE


In addition, this image showcases the relationship between electric fields and electric potential. If you take the negative gradient of electric potential, the result is the electric field. The gradient is the direction of the hills seen in the graph representing electric potential.

Examples

Simple

Questions 1 and 2 are based on the following situation:

A path consists of two locations. Location 1 is at <0.1,0,0>m and Location 2 is at <0.5,0,0>m. A uniform electric field of <300,0,0> N/C exists in this region pointing from Location 1 to Location 2.

Question 1: What is the difference in electric potential between the two points?

[math]\displaystyle{ \Delta{L} }[/math] = final location - initial location = <0.5, 0,0 > - <0.1, 0, 0> = <0.4, 0, 0> m
[math]\displaystyle{ \Delta{V} }[/math] = -[math]\displaystyle{ \vec{E} }[/math]●[math]\displaystyle{ \Delta \vec{l} }[/math] = -([math]\displaystyle{ E_{x} }[/math]●[math]\displaystyle{ \Delta x }[/math] + [math]\displaystyle{ E_{y} }[/math]●[math]\displaystyle{ \Delta y }[/math] + [math]\displaystyle{ E_{z} }[/math]●[math]\displaystyle{ \Delta z }[/math])

= -(300 N/C*.4 + 0*0 + 0*0) = -120

Answer: -120 V


Question 2: What is the change in electric potential energy for a proton on this path?

dU = dV*q = -120 V * 1.6e-19 C = -1.92e-17 J

Answer: - 1.92e-17 J

Middling

figure 1:

Key Point to remember about signs:

1) If the path is going in the direction of the electric field, electric potential is decreasing.

Ex: Refer to Simple Example
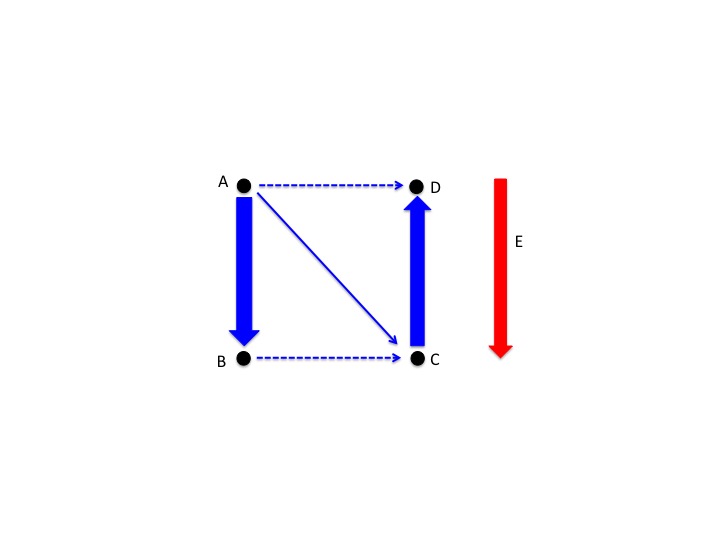
Ex 2: Figure 1
    - Consider the path going from point A to point B. The path is in the same direction as the electric field (red arrow). 
      Because ΔV = -E●Δl = -E●Δr(A->B) = -E●d. This then refers ΔV = Vb-Va < 0, meaning that the electric potential is decreasing.

2) If the path is going in the opposite direction of the electric field, electric potential is increasing.

Question: Location 1 is at <.1,0,0> and Location 2 is at <.5,0,0>. The uniform electric field is <300,0,0> N/C. The charge travels from Location 2 to Location 1.
new dl = <.1,0,0> - <.5,0,0> = <-.4,0,0>m
dV = -Exdx = -(-.4*300) = +120V
Answer: + 120 V
Ex 2: Figure 1
   - Refer back to the figure 1 above. If the path from point C to D was taken, it is going in the opposite direction of the electric field, which means that ΔV > 0;
     therefore, the potential is increasing.

3) If the path is perpendicular to the electric field, electric potential does not change.

Question: Location 1 is at <.1,0,0> and Location 2 is at <.5,0,0>. The uniform electric field is <0,300,0> N/C. The charge travels from Location 1 to Location 2.
new dL = <.5,0,0> - <.1,0,0> = <.4,0,0>m
dV = -(Exdx + Eydy + Exdz) = -(.4*0 + 0*300 +0*0) = 0 V
Answer: 0V
Ex 2: Figure 1
     - Refer back to the figure 1 above. If the path is going from point B to C, or (point A to D), these points are perpendicular to the electric field. Because no work is required to move a 
     a charge between them, all points that are perpendicular to same electric field share same electric potential.

Difficult

The difficult example will refer to using a path that is not directly parallel to the electric field.

Question: Assume an electric field that has a magnitude of 300 N/C. The electric field is uniform. The path chosen is 5 m, 50 degrees away from the field. What is the difference in electric potential in this situation?

dV = -E*dl = -E*l*cos(theta)
dV = -(300 N/C)*(5 m)*cos(50) = -964 V

Answer: -964 V

Connectedness

How is this topic connected to something that you are interested in?

Potential difference is extremely applicable and interesting to me because I am a computer engineer and as a computer engineer, I deal with many things regarding electricity. I am particularly interested in building electric guitar pedals. In addition to the digital signal processing and programming aspect of guitar pedals, there is a lot of physics involved with how they work. Potential difference and electric potential kick in because in addition to the signals that are transmitted throughout the TRS cables, current also runs through them. Obviously, energy and charge are also very prominent in this so they are directly applied to the construction of guitar pedals.

How is it connected to your major?

As a computer engineer, in class and ideally in my job after college, I will be dealing with electronics and electricity in action. I am constantly dealing with breadboards, semiconductors, microprocessors, cables, etc. All of these things essentially require a basic understanding of physics topics especially related to electromagnetism.

Is there an interesting industrial application?

An interested industrial application of electric potential is the ability to use electric potential sensors in human body electrophysiology. In a study conducted by the Center for Physical Electronics and Quantum Technology, the team utilized these sensors to detect electric signals in the human body. The sensors were mainly built with electrometer amplifiers. Specific to electric potential, the senors focus on displacement current rather than electric current at certain locations. The following signals were detected: electrocardiograms, electroencephalograms, and electro-oculograms, and the sensors were able to find the three signals without directly touching the human body. With these findings, the scientists are able to create "spatio-temporal array imaging" of different areas of the human body, including the heart and brain!

History

-Alessandro Volta, and Italian physicist, contributed many ideas and inventions to the field of electricity. He invented the first electric battery, the first electromotive series, and most notably, contributed to the idea of electric potential and its unit, the volt.

-In 1745, Volta was born. He spent most of his childhood experimenting with electricity in his friend's physics lab. When he was 18, he started communicating with physicists, Jean-Antonie Nollet and Giambatista Beccaria, who encouraged him to continue with his experiments.

-In 1775, Volta began teaching physics. He soon was able to isolate methane gas, which he discovered could produce electric sparks. In 1776, Volta put the two ideas together to conclude that he could send electric signals across Italy with the sparking machine.

-In 1778, Volta discovered electric potential, or voltage. He realized that the electric potential in a capacitor is directly proportional to the electric charge in that capacitor.

-In 1800, Volta combined all of his findings to create the voltaic pile, or the first electrochemical cell. This battery made of zinc and copper was able to produce a steady and constant electric current.

-Batteries today serve as the major practical application of electric potential. The unit for electric potential, the Volt, is named after Alessandro Volta and his contributions to the field of electricity.

See also

Further reading

Books, Articles or other print media on this topic

-Electric Potential Difference across a cell membrane:

https://www.google.com/webhp?sourceid=chrome-instant&ion=1&espv=2&ie=UTF-8#q=electric+potential+difference+journal+articles

-Electric Potential Difference between ion phases:

http://pubs.acs.org/doi/abs/10.1021/j150300a003

External links

Internet resources on this topic

This video that walks through examples on potential difference in a uniform field:

https://www.youtube.com/watch?v=mF3VAjcjvOA

This video further discusses electric potential and its concepts:

https://www.youtube.com/watch?v=wT9AsY79f1k

This video on electric potential energy gives a good background on solving problems before learning specifically about electric potential:

https://www.khanacademy.org/science/physics/electric-charge-electric-force-and-voltage/electric-potential-voltage/v/electric-potential-energy

References

-http://study.com/academy/lesson/what-is-electric-potential-definition-formula-quiz.html

-http://www.famousscientists.org/alessandro-volta/

-http://www.isipt.org/world-congress/3/269.html

-http://maxwell.ucdavis.edu/~electro/potential/overview.html

-Matter & Interactions Vol II: Electric and Magnetic Interactions textbook

Retrieved from "http://www.physicsbook.gatech.edu/index.php?title=Potential_Difference_in_a_Uniform_Field&oldid=39082"