Magnetic Flux

Claimed by Rahul Singi (Spring 2017)

Claimed by Vansh Kareer (Fall 2017)

Claimed by Patricia Estrada (Spring 2018)

The Main Idea

A Mathematical Model

Recall that according to Gauss's law, the electric flux through any closed surface is directly proportional to the net electric charge enclosed by that surface. Given the very direct analogy which exists between an electric charge and a magnetic 'monopoles', we would expect to be able to formulate a second law which states that the magnetic flux through any closed surface is directly proportional to the number of magnetic monopoles enclosed by that surface. But the problem is that magnetic monopoles don't exist. It follows that the equivalent of Gauss's law for magnetic fields reduces to:

[math]\displaystyle{ \Phi_B = \oint B \cdot dA = 0 }[/math]

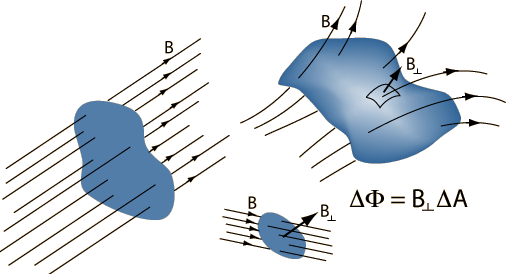
Realistically, the magnetic flux though any CLOSED surface is zero. The magnetic flux through an area will be its own individual value. This rule is useful when solving for a an unknown magnetic field that's coming from a side of a surface when the other fields from the other sides are known. Magnetic flux is measured in SI units of Weber (Wb), named after German physicist and co-inventor of the telegraph Wilhelm Weber.

This is the Gauss's law general form for finding magnetic flux through an area (not closed surface).

[math]\displaystyle{ \Phi_B = \oint B \cdot dA }[/math]

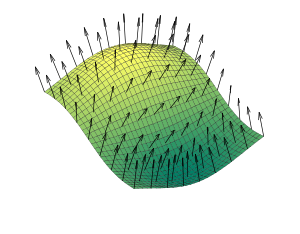
To fully understand the meaning of this equation, an understanding of normal vectors and dot products is required. Relative to a surface, a normal vector runs perpendicular to the surface at a certain point. For currved surfaces, such as the one shown below, there are many different normal vectors for each plane of the surface.

Thus Gauss's law for magnetic flux can be expanded via the dot product definition, where theta is the angle between the plane of the surface area and the vector of magnetic field at that location.

[math]\displaystyle{ \Phi_B = \oint B \cdot dA =\oint B * dA * cos(\theta) }[/math]

A Computational Model

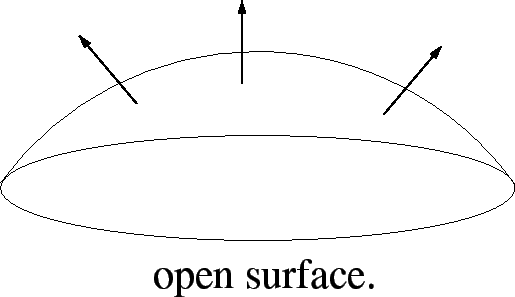
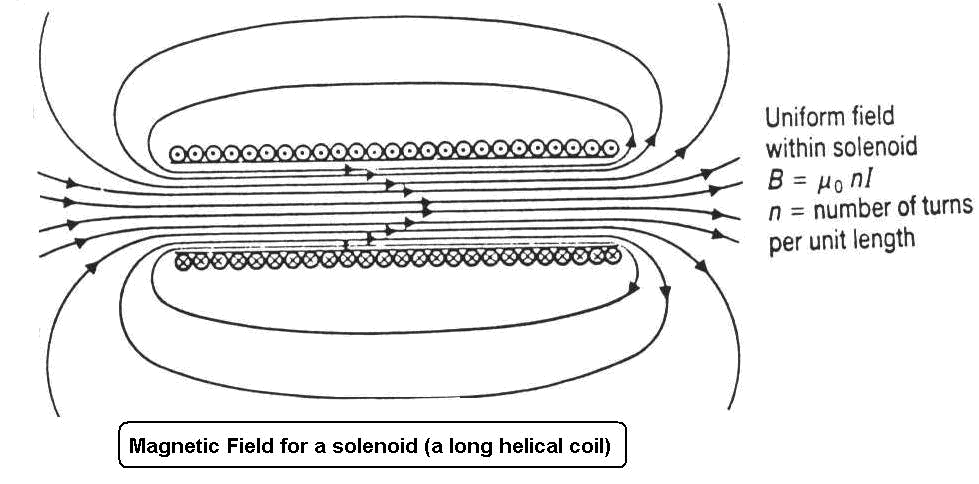
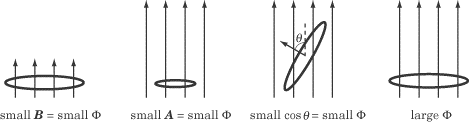
As seen on the formula described on the section above, the magnetic flux of an object depends on the size and shape of the object. Therefore, it is hard to show one specific computational model that can correctly illustrate magnetic flux. However, below are some images that show the magnetic flux of three common types of surfaces: closed, open, and solenoid.

A closed surface:

An open surface:

Solenoid:

Further Description

Gauss's Law for magnetism tells us that magnetic monopoles do not exist. If magnetic monopoles existed, they would be sources and sinks of the magnetic field, and therefore the right-hand side could differ from zero. Gauss's Law for magnetism is one of the four Maxwell's equations, which form the foundation for the entire theory of classical electrodynamics.

The magnitude of the magnetic flux depends on the strength of the magnetic field, the size of the surface area, and the angle between the direction in which the surface area points and the direction of the magnetic field (the definition of a dot-product; only the component of the magnetic field nromal to the surface is considered).

As stated before, another of Maxwell's equations, Gauss's Law for electric fields, concerns electric field flux.

[math]\displaystyle{ \Phi_E = \iint_S E \cdot dS = \dfrac{Q}{\epsilon_0} }[/math]

Here, [math]\displaystyle{ \Phi_E }[/math] represents electric field flux, E represent the electric field present, S represents the closed surface area being considered, Q is the total electric charge encompassed by the surface area, and [math]\displaystyle{ \epsilon_0 }[/math] is the electric constant (known as the permittivity of free space). Thus, the electric field through a closed surface area is not always zero, unlike the magnetic flux through a closed surface, which is zero due to the lack of existence of magnetic monopoles. This electric field flux equation is the opposite of Gauss's law for magnetic flux, indicating the importance of electric monopoles (free positive and negative charges) to electric field flux.

Applications

Magnetic flux is very closely related to electric flux using Gauss's law for electric fields (one of the four Maxwell equations).

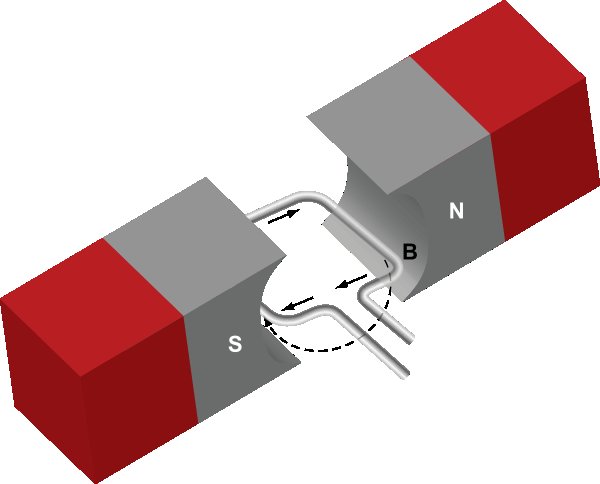
There are a few important real-world applications of magnetic flux. As described by Faraday's Law, when a coiled wire moves through a magnetic field, a voltage is produced. This voltage is dependent on the magnetic flux (due to the surrounding magnetic field) through the area of the coiled wire, as seen below.

Via the Faraday-Lenz law, engineers can easily calculate the voltage generated by a coiled wire in a magnetic field. The relationship is electro-motive force equals the negative rate of change of magnetic flux over time.

[math]\displaystyle{ \epsilon = -\dfrac{d\Phi}{dt} }[/math]

Practice Problems

Walkthroughs

Simple Walthrough:[1]

Middling Walkthrough: [2]

Advanced Walkthrough: [3]

Once you get the hang of the process of solving magnetic flux problems using the walkthroughs, try some of the basic questions, then move on to the more advanced questions below.

Basic

1) As shown below, there a current-carrying wire alongside a coil of wire. Using Gauss's Law, calculate the magnitude of magnetic flux through the coil of wire. [Question from Khan Academy; solution through link below]

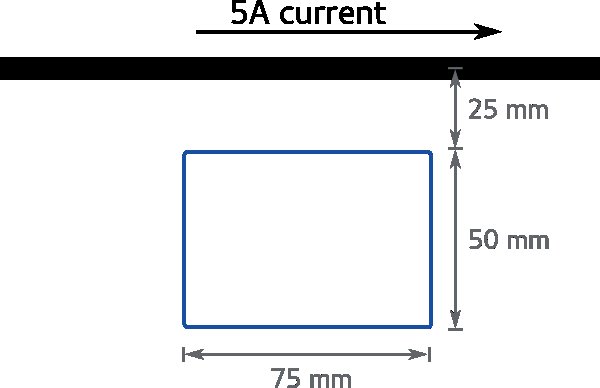
2) Calculate the magnetic flux through the coiled wire given the magnetic field present.

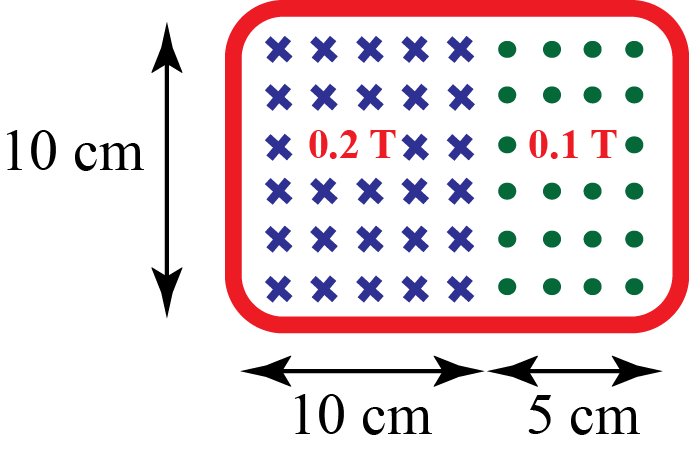
3) Calculate the magnetic flux through the coiled wire given the magnetic fields present.

4) A wire of resistance 7 ohms and length 3.8 m is bent into a circle and is concentric with a solenoid in which the magnetic flux changes from 5 T·m2 to 3 T·m2 in 0.2 seconds. What is the emf in the wire?

Advanced

1) There is a small bar magnet with a magnetic dipole D located at the origin (0,0,0). It's aligned with the y-axis. There is a circular disk with a radius of R facing perpendicular to the yz plane and its center is 4 meters away on the +x axis from the bar magnet. What is the magnetic flux going through the disk in terms of the given variable? (Consult with your professor for the solution).

2) Referring back to the previous problem, the disk is now tilted so that the angle between the yz plane and the surface is 30 degrees. Find the new magnetic flux in terms of the given variables.

3) A square with side length T is directly facing the xy plane 3 meters away from a current carrying 1 meter wire (from a portion of a nearby circuit powered by a battery with an emf of U). The wire is aligned with the y axis. The magnetic flux going through the square is G. Find the resistance of the wire.

Solutions

Basic

1) Khan Academy: [4]

2) Use the base form of Gauss's Law of magnetic flux.

[math]\displaystyle{ \Phi_B = \oint B \cdot dA }[/math]

[math]\displaystyle{ dA=0.02 m *0.04 m= 0.0008 m^2 }[/math]

[math]\displaystyle{ \Phi_B = \oint B \cdot dA=0.2 T * 0.0008 m^2= 0.00016 T*m^2=0.00016 Wb }[/math]

3) Here, employ the same method as the last problem, but remember that the two magnetic fields run in opposite directions.

[math]\displaystyle{ \Phi_B = \oint B \cdot dA }[/math]

[math]\displaystyle{ dA=0.1 m *0.15 m= 0.015 m^2 }[/math]

[math]\displaystyle{ \Phi_B = \oint B \cdot dA=(0.2-0.1) T * 0.015 m^2= 0.0015 T*m^2=0.0015 Wb }[/math]

4) Recall that magnitude of electro-motive force equals the change in magnetic flux over time.

[math]\displaystyle{ \epsilon = \dfrac{d\Phi}{dt} }[/math]

[math]\displaystyle{ \epsilon = \dfrac{(5 T*m^2-3 T*m^2)}{(0.2 s)} = 10 V }[/math]

History

A major part of the history of magnetic flux is tied to Carl Freidrich Gauss. Gauss was a 19th century German physicist and mathematician that had notable contributions in not only the world of physics but across the fields of algebra, astronomy, and geometry. However, in this course, he is mainly known for the introduction of one of the four Maxwell's Laws(partial differential equations), titled Gauss's Law which describes the equation used to calculate magnetic flux.

Prior to Gauss's study on the subject however, Joseph-Louis Lagrange (famous Italian mathematician) had studied the subject. However, Gauss completed the formulation of the theory and published it in 1813.

Lagrange:

Gauss:

Further Reading

What is Magnetic Flux?: [5]

Overview: [6]

In-Depth Tutorial: [7]

Helpful Links/Videos

Khan Academy: [8]

Quick Explanation: [9]

In-Depth Explanation: [10]

Another Problem: [11]

References

Pictures: [12]

Pictures: [13]

Pictures: [14]

Pictures: [15]

Pictures: [16]

Picture: [17]

Picture: [18]

Picture: [19]

Picture: [20]

WebAssign Instructional Application for PHYS 2212, Georgia Institute of Technology.

Resource : [21]

Resource: [22]

Picture: [23]