Gravitational Force Near Earth: Difference between revisions
No edit summary |
|||
| Line 1: | Line 1: | ||
'''[William Beard Fall 2021]''' This section describes gravitational force near Earth's surface, including applications and relevant derivations. | |||
==Main Idea== | |||
=== A Mathematical Model === | Near Earth's surface, the magnitude of acceleration due gravity is approximately constant. Newton's Law of Universal Gravitation states that any two bodies attract each other with a force directly proportional to the product of the masses and inversely proportional to the square of the distance between the objects. If we approximate the Earth as a point mass, we find that the distance to the surface is simply the radius of the Earth. We now want to apply Newton's Law of Universal Gravitation to our approximation and see if we can calculate the acceleration due to gravity near Earth's surface. Generally this is only acceptable because the distance between the object of interest and Earth's surface is <math> << </math> the distance from the center of the Earth to Earth's surface. Thus the difference in distances is so small that the result is well-approximated using only Earth's radius. | ||
===A Mathematical Model=== | |||
From Newton's Law of Universal Gravitation we know: | |||
::<math> {F}_{grav}=G \frac{m_1 m_2}{r^2}\ </math> | ::<math> {F}_{grav}=G \frac{m_1 m_2}{r^2}\ </math> | ||
| Line 13: | Line 13: | ||
::* ''m''<sub>1</sub> is the mass of the first object; | ::* ''m''<sub>1</sub> is the mass of the first object; | ||
::* ''m''<sub>2</sub> is the mass of the second object; | ::* ''m''<sub>2</sub> is the mass of the second object; | ||
::* ''r'' is the distance between the | ::* ''r'' is the distance between the objects. | ||
Near Earth's surface, however, <math> \frac{GM_{Earth}}{R_{Earth}^2}</math> is | Near Earth's surface, however, <math> \frac{GM_{Earth}}{R_{Earth}^2}</math> is unchanging. As such, we define it as the gravitational constant near Earth's surface, ''g'', which is approximately <math>9.8 \frac{m}{s^2} </math>. This calculation is shown below: | ||
::<math> g = \frac{GM_{Earth}}{R_{Earth}^2}= \frac{(6.67*10^{-11} \frac{m^3}{kgs})(5.972*10^{24} kg)}{(6.378*10^{6} m)^2} = 9.8 \frac{m}{s^2}</math> | ::<math> g = \frac{GM_{Earth}}{R_{Earth}^2}= \frac{(6.67*10^{-11} \frac{m^3}{kgs})(5.972*10^{24} kg)}{(6.378*10^{6} m)^2} = 9.8 \frac{m}{s^2}</math> | ||
| Line 24: | Line 24: | ||
::* ''g'' is the near-Earth gravitational constant, as defined above to be <math>9.8 \frac{m}{s^2} </math> | ::* ''g'' is the near-Earth gravitational constant, as defined above to be <math>9.8 \frac{m}{s^2} </math> | ||
::* ''m'' is the mass of the object whose behavior we are interested in | ::* ''m'' is the mass of the object whose behavior we are interested in | ||
===A Computational Model=== | |||
Using the approximation derived above, we can create a computational model for the force of gravity near Earth's surface by applying Newton's second law in an iterative fashion to update acceleration, velocity, and finally position. This allows us to simulate the motion of an object near Earth's surface using only its mass. Seen below is a GlowScript code snippet accomplishing this iterative update technique. | |||
<code> | |||
::Fnet = vector(0, -g, 0) | |||
::ball.vel = ball.vel + Fnet / ball.m * deltat | |||
::ball.pos = ball.pos + ball.vel * deltat | |||
</code> | |||
==Examples== | ==Examples== | ||
=== | ===Introductory=== | ||
''Suppose a 50 kg man | ''Suppose a 50 kg man stands on the Earth's surface. What is the magnitude of the gravitational force experienced by the man?'' | ||
First notice that since we are near Earth's surface, it is appropriate to use our approximation of gravitational force rather than Newton's Law of Universal Gravitation. As such, recall <math>|\vec{\mathbf{F}}_{grav}|= mg </math>. Here, ''m'' is equal to 50 kg, and ''g'' is equal to <math> 9.8 \frac{m}{s^2}</math>. This means that: | |||
:: <math>|\vec{\mathbf{F}}_{grav}|= mg = (50 kg)(9.8 \frac{m}{s^2}) = 490 N </math> | :: <math>|\vec{\mathbf{F}}_{grav}|= mg = (50 kg)(9.8 \frac{m}{s^2}) = 490 N </math> | ||
=== | ===Intermediate=== | ||
''A person is laying on their back and pushing a 20 kg weight straight up (they're bench pressing the weight). What is the magnitude of the force they must be exerting on the weight if the weight is moving straight up without any acceleration?'' | ''A person is laying on their back and pushing a 20 kg weight straight up (they're bench pressing the weight). What is the magnitude of the force they must be exerting on the weight if the weight is moving straight up without any acceleration?'' | ||
We know from Newton's Second Law that force is directly proportional to acceleration. Thus if acceleration is zero, net force must also be zero and the weight will move at a constant velocity. This means that the force exerted by the person must be equal in magnitude to the force of gravity on the object (since they act in exactly opposite directions). | |||
::<math>F_{g}=F_{person}=mg</math> | ::<math>F_{g}=F_{person}=mg</math> | ||
::<math>F_{person}=(20 kg)(9.8 \frac{m}{s^2})=196 N</math> | ::<math>F_{person}=(20 kg)(9.8 \frac{m}{s^2})=196 N</math> | ||
=== | ===Advanced=== | ||
''Suppose a 60 kg person is standing in an elevator that is accelerating upwards at <math> 1 \frac{m}{s^2}</math>. If they are standing on a scale, what does that scale read while the elevator accelerates upwards? A picture illustrating the situation is attached.'' | ''Suppose a 60 kg person is standing in an elevator that is accelerating upwards at <math> 1 \frac{m}{s^2}</math>. If they are standing on a scale, what does that scale read while the elevator accelerates upwards? A picture illustrating the situation is attached.'' | ||
[[File:Elevator_near_earth.png|200px|thumb|right|This diagram illustrates the | [[File:Elevator_near_earth.png|200px|thumb|right|This diagram illustrates the situation, where F sub n is the normal force.]] | ||
Here, the net acceleration is the same as that of the elevator, which is <math> 1 \frac{m}{s^2} </math>. The mass is | Here, the net acceleration is the same as that of the elevator, which is <math> 1 \frac{m}{s^2} </math>. The mass is 60 kg. In order to determine the weight that the scale reads, we must look at the normal force exerted by the scale. | ||
The above means that the net force is in the upwards direction. | The above means that the net force is in the upwards direction. | ||
| Line 53: | Line 62: | ||
::<math>F_{N}=(60 kg)(1 \frac{m}{s^2} +9.8 \frac{m}{s^2}) = 648 N </math> | ::<math>F_{N}=(60 kg)(1 \frac{m}{s^2} +9.8 \frac{m}{s^2}) = 648 N </math> | ||
== | ==Importance== | ||
Understanding gravity and its applications is fundamental to building intuition for our universe. On a small scale, we can use our knowledge of Earth's intrinsic qualities to simplify many basic physics problems and better understand the world around us, but the approximation scheme described here can be used for any (relatively uniform) bodies, including other planets in our solar system, extending its usefulness to beyond just Earth's surface. In particular, the ideas in this article help to show why a scale would show different values depending upon the planet on which it's placed (try calculating your weight on the moon, for instance). | |||
From an industrial perspective, understanding gravitational force near Earth's surface is important because it may affect the design process for various products. When designing a bridge, for instance, one must verify that the force on the bridge due to gravity will not be strong enough to undermine the bridge's stability. Even when making a lamp it's important to check that a joint is powerful enough to withstand the torque experienced by the object due to the force of gravity near Earth's surface. | |||
==History== | ==History== | ||
Prior to | Prior to the age of Newton, gravity as a force was a totally foreign concept. During the 17th century, Galileo realized that all objects, regardless of mass, fall with the same acceleration towards Earth. It was in 1687 when Newton published his ''Principia'' that he hypothesized that gravity acts as a force whose magnitude is inversely proportional to the square of distance between objects. This description was incomplete, however, and remained unfinished until Cavendish determined the value of ''G'', the universal gravitational constant. | ||
==See Also== | ==See Also== | ||
===Further Reading=== | ===Further Reading=== | ||
::* [https://phys.libretexts.org/Bookshelves/University_Physics/Book%3A_University_Physics_(OpenStax)/Map%3A_University_Physics_I_-_Mechanics%2C_Sound%2C_Oscillations%2C_and_Waves_(OpenStax)/13%3A_Gravitation/13.2%3A_Gravitation_Near_Earth's_Surface Gravitation Near Earth's Surface] | |||
===External Links=== | |||
::* [https://en.wikipedia.org/wiki/History_of_gravitational_theory History of Gravitational Theory] | ::* [https://en.wikipedia.org/wiki/History_of_gravitational_theory History of Gravitational Theory] | ||
::* [http://hyperphysics.phy-astr.gsu.edu/hbase/grav.html#grav Hyperphysics Gravity] | ::* [http://hyperphysics.phy-astr.gsu.edu/hbase/grav.html#grav Hyperphysics Gravity] | ||
==References== | |||
Revision as of 23:40, 5 December 2021
[William Beard Fall 2021] This section describes gravitational force near Earth's surface, including applications and relevant derivations.
Main Idea
Near Earth's surface, the magnitude of acceleration due gravity is approximately constant. Newton's Law of Universal Gravitation states that any two bodies attract each other with a force directly proportional to the product of the masses and inversely proportional to the square of the distance between the objects. If we approximate the Earth as a point mass, we find that the distance to the surface is simply the radius of the Earth. We now want to apply Newton's Law of Universal Gravitation to our approximation and see if we can calculate the acceleration due to gravity near Earth's surface. Generally this is only acceptable because the distance between the object of interest and Earth's surface is [math]\displaystyle{ \lt \lt }[/math] the distance from the center of the Earth to Earth's surface. Thus the difference in distances is so small that the result is well-approximated using only Earth's radius.
A Mathematical Model
From Newton's Law of Universal Gravitation we know:
- [math]\displaystyle{ {F}_{grav}=G \frac{m_1 m_2}{r^2}\ }[/math]
- where,
- F is the gravitational force between the masses;
- G is the gravitational constant, [math]\displaystyle{ 6.674×10^{−11} \frac{N m^2}{kg^2}\ }[/math];
- m1 is the mass of the first object;
- m2 is the mass of the second object;
- r is the distance between the objects.
Near Earth's surface, however, [math]\displaystyle{ \frac{GM_{Earth}}{R_{Earth}^2} }[/math] is unchanging. As such, we define it as the gravitational constant near Earth's surface, g, which is approximately [math]\displaystyle{ 9.8 \frac{m}{s^2} }[/math]. This calculation is shown below:
- [math]\displaystyle{ g = \frac{GM_{Earth}}{R_{Earth}^2}= \frac{(6.67*10^{-11} \frac{m^3}{kgs})(5.972*10^{24} kg)}{(6.378*10^{6} m)^2} = 9.8 \frac{m}{s^2} }[/math]
This then puts the force near Earth due to gravity into a much simpler form:
- [math]\displaystyle{ |\vec{\mathbf{F}}_{grav}|= mg }[/math]
- where,
- g is the near-Earth gravitational constant, as defined above to be [math]\displaystyle{ 9.8 \frac{m}{s^2} }[/math]
- m is the mass of the object whose behavior we are interested in
A Computational Model
Using the approximation derived above, we can create a computational model for the force of gravity near Earth's surface by applying Newton's second law in an iterative fashion to update acceleration, velocity, and finally position. This allows us to simulate the motion of an object near Earth's surface using only its mass. Seen below is a GlowScript code snippet accomplishing this iterative update technique.
- Fnet = vector(0, -g, 0)
- ball.vel = ball.vel + Fnet / ball.m * deltat
- ball.pos = ball.pos + ball.vel * deltat
Examples
Introductory
Suppose a 50 kg man stands on the Earth's surface. What is the magnitude of the gravitational force experienced by the man?
First notice that since we are near Earth's surface, it is appropriate to use our approximation of gravitational force rather than Newton's Law of Universal Gravitation. As such, recall [math]\displaystyle{ |\vec{\mathbf{F}}_{grav}|= mg }[/math]. Here, m is equal to 50 kg, and g is equal to [math]\displaystyle{ 9.8 \frac{m}{s^2} }[/math]. This means that:
- [math]\displaystyle{ |\vec{\mathbf{F}}_{grav}|= mg = (50 kg)(9.8 \frac{m}{s^2}) = 490 N }[/math]
Intermediate
A person is laying on their back and pushing a 20 kg weight straight up (they're bench pressing the weight). What is the magnitude of the force they must be exerting on the weight if the weight is moving straight up without any acceleration?
We know from Newton's Second Law that force is directly proportional to acceleration. Thus if acceleration is zero, net force must also be zero and the weight will move at a constant velocity. This means that the force exerted by the person must be equal in magnitude to the force of gravity on the object (since they act in exactly opposite directions).
- [math]\displaystyle{ F_{g}=F_{person}=mg }[/math]
- [math]\displaystyle{ F_{person}=(20 kg)(9.8 \frac{m}{s^2})=196 N }[/math]
Advanced
Suppose a 60 kg person is standing in an elevator that is accelerating upwards at [math]\displaystyle{ 1 \frac{m}{s^2} }[/math]. If they are standing on a scale, what does that scale read while the elevator accelerates upwards? A picture illustrating the situation is attached.
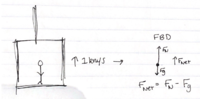
Here, the net acceleration is the same as that of the elevator, which is [math]\displaystyle{ 1 \frac{m}{s^2} }[/math]. The mass is 60 kg. In order to determine the weight that the scale reads, we must look at the normal force exerted by the scale.
The above means that the net force is in the upwards direction.
- [math]\displaystyle{ |\vec{\mathbf{F}}_{net}|=F_{N}-mg=ma }[/math]
- [math]\displaystyle{ F_{N}=m(a+g) }[/math]
- [math]\displaystyle{ F_{N}=(60 kg)(1 \frac{m}{s^2} +9.8 \frac{m}{s^2}) = 648 N }[/math]
Importance
Understanding gravity and its applications is fundamental to building intuition for our universe. On a small scale, we can use our knowledge of Earth's intrinsic qualities to simplify many basic physics problems and better understand the world around us, but the approximation scheme described here can be used for any (relatively uniform) bodies, including other planets in our solar system, extending its usefulness to beyond just Earth's surface. In particular, the ideas in this article help to show why a scale would show different values depending upon the planet on which it's placed (try calculating your weight on the moon, for instance).
From an industrial perspective, understanding gravitational force near Earth's surface is important because it may affect the design process for various products. When designing a bridge, for instance, one must verify that the force on the bridge due to gravity will not be strong enough to undermine the bridge's stability. Even when making a lamp it's important to check that a joint is powerful enough to withstand the torque experienced by the object due to the force of gravity near Earth's surface.
History
Prior to the age of Newton, gravity as a force was a totally foreign concept. During the 17th century, Galileo realized that all objects, regardless of mass, fall with the same acceleration towards Earth. It was in 1687 when Newton published his Principia that he hypothesized that gravity acts as a force whose magnitude is inversely proportional to the square of distance between objects. This description was incomplete, however, and remained unfinished until Cavendish determined the value of G, the universal gravitational constant.