Fourier Series and Transform: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
A Fourier | A Fourier Series is an expansion of trigonometric functions to model periodic functions. This method proves useful in the study of harmonic systems as the analysis in a more familiar domain is much simpler than in its original domain. It has a variety of applications ranging from signal processing to quantum mechanics. The Fourier Series is defined as: <br><math>f(x)=\sum_{n=1}^{\infty}{a_n\cos{(\frac{n\pi x}{L}})}+\sum_{n=1}^{\infty}{b_n\sin{(\frac{n\pi x}{L}})}</math><br> for <math>x\in[-L,L]</math> | ||
==Intuition== | ==Intuition== | ||
Many physical systems can be modeled by square waves. Consider systems with on-off behavior, similar to an on-and-off switch. A sine wave and square wave looks like this respectively:<br> | Many physical systems can be modeled by square waves. Consider systems with on-off behavior, similar to an on-and-off switch. A sine wave and square wave looks like this respectively:<br> | ||
[[File:sinewave.png|400px|]][[File:Arrow.png|200px|]][[File:squarewave.png|300px|]]<br> | [[File:sinewave.png|400px|]][[File:Arrow.png|200px|]][[File:squarewave.png|300px|]]<br> | ||
As the diagram hints, we can use the Fourier Series to get from the sine wave to the square wave. Consider this progression of solely sine functions. We know what <math>f(x)=\sin(x)</math> looks like. If we keep adding a term in the partial sum for all odd integers of <math>f(x)=\frac{\sin(nx)}{n}</math>, the development of the square wave is noticeable as n increases:<br> | As the diagram hints, we can use the Fourier Series to get from the sine wave to the square wave. Consider this progression of solely sine functions. We know what <math>f(x)=\sin(x)</math> looks like. If we keep adding a term in the partial sum for all odd integers of <math>f(x)=\frac{\sin(nx)}{n}</math>, the development of the square wave is noticeable as n increases:<br> | ||
[[File:Squarewavee_(3).png|300px|]] <br>The darker function is <math>f(x)=\sin(x)</math> and the lighter function is the partial sum of the series to the fifth term. As you can see, the series function is beginning to look more like a square as <math>n \to \infty</math>. In using a | [[File:Squarewavee_(3).png|300px|]] <br>The darker function is <math>f(x)=\sin(x)</math> and the lighter function is the partial sum of the series to the fifth term. As you can see, the series function is beginning to look more like a square wave as <math>n \to \infty</math>. In using a summation of sines (and\or cosines), we can eventually reach the square wave. | ||
==Finding Coefficients== | |||
If we take the formula for a general Fourier Series, we can manipulate it to derive the formulas for <math> a_1, a_n, </math> and <math>b_n</math><br> | |||
We have <math>f(x)=\sum_{n=1}^{\infty}{a_n\cos{(\frac{n\pi x}{L}})}+\sum_{n=1}^{\infty}{b_n\sin{(\frac{n\pi x}{L}})}</math><br> for <math>x\in[-L,L]</math><br> | |||
<br>Multiply both sides by <math>\cos{(\frac{m\pi x}{L})}</math> and integrate both sides for <math> x\in[-L,L] </math>: | |||
<br><br><math>\int_{-L}^{L}{f(x)\cos{(\frac{m\pi x}{L})}}dx=\sum_{n=1}^{\infty}{a_n\int_{-L}^{L}{\cos{(\frac{n\pi x}{L}})\cos{(\frac{m\pi x}{L}})}}dx+\sum_{n=1}^{\infty}{b_n\int_{-L}^{L}{\sin{(\frac{n\pi x}{L}})\cos{(\frac{m\pi x}{L})}}}dx</math> | |||
Revision as of 01:37, 6 December 2022
A Fourier Series is an expansion of trigonometric functions to model periodic functions. This method proves useful in the study of harmonic systems as the analysis in a more familiar domain is much simpler than in its original domain. It has a variety of applications ranging from signal processing to quantum mechanics. The Fourier Series is defined as:
[math]\displaystyle{ f(x)=\sum_{n=1}^{\infty}{a_n\cos{(\frac{n\pi x}{L}})}+\sum_{n=1}^{\infty}{b_n\sin{(\frac{n\pi x}{L}})} }[/math]
for [math]\displaystyle{ x\in[-L,L] }[/math]
Intuition
Many physical systems can be modeled by square waves. Consider systems with on-off behavior, similar to an on-and-off switch. A sine wave and square wave looks like this respectively:
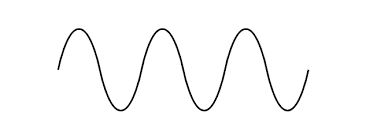

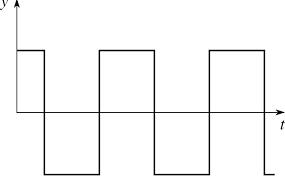
As the diagram hints, we can use the Fourier Series to get from the sine wave to the square wave. Consider this progression of solely sine functions. We know what [math]\displaystyle{ f(x)=\sin(x) }[/math] looks like. If we keep adding a term in the partial sum for all odd integers of [math]\displaystyle{ f(x)=\frac{\sin(nx)}{n} }[/math], the development of the square wave is noticeable as n increases:
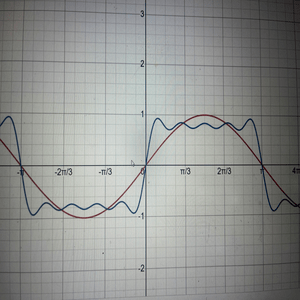
The darker function is [math]\displaystyle{ f(x)=\sin(x) }[/math] and the lighter function is the partial sum of the series to the fifth term. As you can see, the series function is beginning to look more like a square wave as [math]\displaystyle{ n \to \infty }[/math]. In using a summation of sines (and\or cosines), we can eventually reach the square wave.
Finding Coefficients
If we take the formula for a general Fourier Series, we can manipulate it to derive the formulas for [math]\displaystyle{ a_1, a_n, }[/math] and [math]\displaystyle{ b_n }[/math]
We have [math]\displaystyle{ f(x)=\sum_{n=1}^{\infty}{a_n\cos{(\frac{n\pi x}{L}})}+\sum_{n=1}^{\infty}{b_n\sin{(\frac{n\pi x}{L}})} }[/math]
for [math]\displaystyle{ x\in[-L,L] }[/math]
Multiply both sides by [math]\displaystyle{ \cos{(\frac{m\pi x}{L})} }[/math] and integrate both sides for [math]\displaystyle{ x\in[-L,L] }[/math]:
[math]\displaystyle{ \int_{-L}^{L}{f(x)\cos{(\frac{m\pi x}{L})}}dx=\sum_{n=1}^{\infty}{a_n\int_{-L}^{L}{\cos{(\frac{n\pi x}{L}})\cos{(\frac{m\pi x}{L}})}}dx+\sum_{n=1}^{\infty}{b_n\int_{-L}^{L}{\sin{(\frac{n\pi x}{L}})\cos{(\frac{m\pi x}{L})}}}dx }[/math]