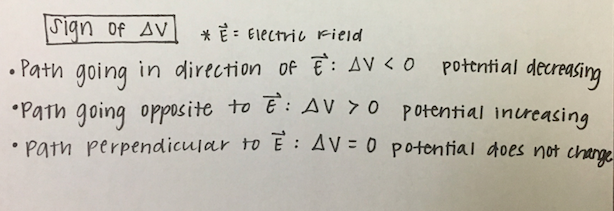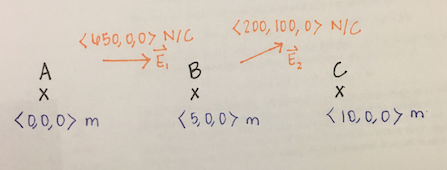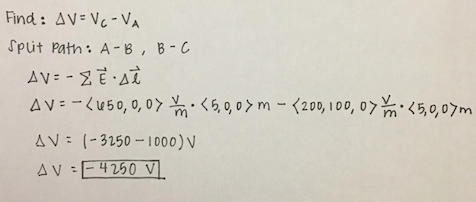Electric Field and Electric Potential
Claimed by Emily Dunford, Fall 2017 The concepts of electric field and electric potential stem from the broader ideas of electricity and electric charge. Introduced by renowned scientist Michael Faraday, the physics of electricity is all around us. We experience the abstract notion of electricity every single day and in every part of the world. The science behind electricity is more than just flipping a switch on and off; it involves the concepts of electric charge, electric field, and electric potential. There are so many calculations, patterns, and ideas that come about from those concepts, but of those electric field and electric potential will allow us to dig deeper into the science behind the most useful physical phenomena of today, electricity.
The Main Idea
In physics, many phenomena that we observe are interrelated in some capacity. In the study of electricity and magnetism, several important physical quantities that play a crucial role in understanding physical interactions are derived from one another. Electric field is a concept that is discussed early in most Electricity and Magnetism curricula, but it has an enormous impact once we discover that it tells us information about electric potential, and from that, potential energy. This helps physicists to understand both the mechanics of a system and the quantized nature of that system.
Electricity is undoubtedly one of the most prominent physical phenomena that we see and use today. This major phenomena stems from the presence of electric charges. An electric charge is a basic property behind the physics of matter and it gives rise to the science of electric and magnetic fields and forces. The two types of electric charge are negative and positive, which come from electrons and protons, respectively. It is the presence of these negative and positive electric charges that causes an electric field to be produced. According to Chabay and Sherwood's Matter and Interactions: Electric and Magnetic Interactions, "the electric field created by a charge is present throughout space at all times, whether or not there is another charge around to feel its effects." Electric potential, which is also known as voltage, is the difference in potential energy per unit charge between two locations in an electric field (Khan Academy). If you recall from earlier physics courses, potential energy is the energy that is stored based on the position of the object. The two concepts of electric field and electric potential are connected because the flow of the electric field is caused by the difference in electric potential.
The electric field is the force field that surrounds electric charges. It attracts or repels other electric charges. Electric fields are created by electric charges and by time dependent magnetic fields. The electric field exerts either an attractive or repulsive force on anything containing an electric charge that is close by. It has units of Newtons per Coulomb. The electric potential is the amount of work required to move a positive charge from a point of reference to another point inside the field without producing acceleration. It has units of Joules per Coulomb.
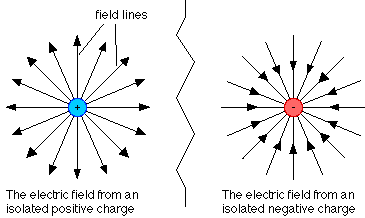
These videos will provide you with more information on Electric Field and Electric Potential:
https://www.youtube.com/watch?v=0YOGrTNgGhE
https://www.youtube.com/watch?v=elJUghWSVh4
A Mathematical Model
We know that the electric force, given by Coulomb's Law, is [math]\displaystyle{ {\vec{F}=q\vec{E}} }[/math]. We also know that electric field and electric force are closely related, the electric field being equal to the electric force divided by the amount of charge [math]\displaystyle{ {\vec{E}=\frac{\vec{F}}{q}} }[/math].
If we think back to the study of conservation of energy, we know that the change in potential energy of a system is work, which is a force being applied over a distance. Since force and distance are vectors, integrating up over the distance of applied force, we obtain: [math]\displaystyle{ {\Delta U=-\int_i^f {\vec{F} • \vec{ds}}} }[/math]. By analogy, we define the electric potential as the energy per coulomb or potential energy divided by charge: [math]\displaystyle{ {\Delta V=-\int_i^f {\vec{E} • \vec{ds}}} }[/math].
Observe both sets of equations: the two for Electric Field and Electric Force, and the two for Electric Potential and Potential Energy. We see that they are all related mathematically. If we integrate the electric force, that is, sum the contributions of force over a finite distance, we obtain the change in potential energy. Dividing by the charge, we obtain the potential difference or electric potential, which we see is simply the integral of the electric field applied over a distance.
Pictured below is an alternative method to write the mathematical formulations for Electric potential. Instead of approaching a problem based on the calculus-based formulations presented above, the calculations below are performed by dot product, a more algebraic approach.
The sign of potential difference is a very critical part of electric potential calculations. The sign depends on the direction of the path relative to the electric field. The rules for the sign of potential difference is presented below.
A Computational Model
We can model how a system will change in electric potential and potential energy as we move, for example, through a uniform electric field in programs like VPython. One could visualize the electric field, electric force, and quantitatively determine the potential and potential energy as, for instance, a system as simple as a single particle moves through space.
Examples
EXAMPLE 1: Potential Difference in Uniform Field
The electric field is uniform in this region and
equal to < 0, –300, 0> N/C. B is at < 2, 2, 0> m and
C is at < 2, 0, 0> m. What is ΔV along a path from B to
C?
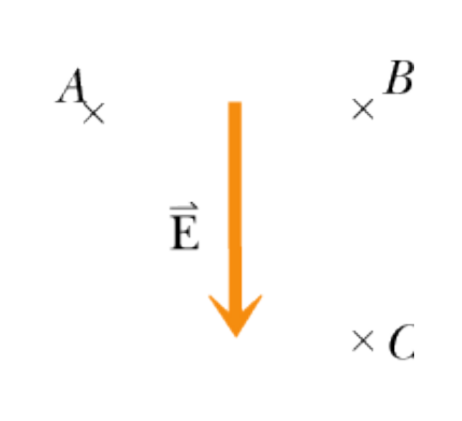
Example 1 Solution
In this problem, we are given the electric field and asked to find the change in potential between those two points. The formula that we must apply here is [math]\displaystyle{ \Delta V = -\int_i^f \vec{E} • d\vec{s} }[/math], where the initial point is B and the final point is C, making the distance <2,0,0> m - <2,2,0> m = <0,-2,0> m.
The change in potential therefore is the dot product of the electric field and the change in distance:
-<0,-300,0> N/C • <0,-2,0> m = -600 V
EXAMPLE 2: Potential Difference in Nonuniform Field
From location A to location B, the electric field is uniform and is <650,0,0> N/C. From location B to location C, the electric field is uniform and is <200,100,0> N/C. What is the potential difference between location A and C? Look at the picture below to get a better visual of the problem.
Example 2 Solution
The best way to approach this problem is to split the path into 2 parts: part 1 - Location A to Location B and part 2 - Location B to Location C. You have to do this because the electric field differs in those 2 regions.
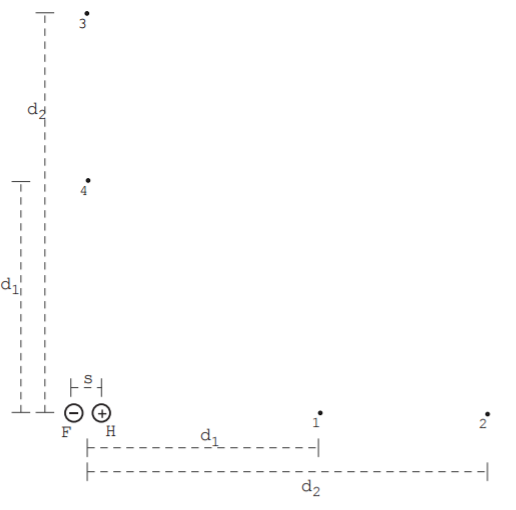
EXAMPLE 3: Potential Difference on Electric Dipole Axis
An HF molecule in the gas phase has an internuclear separation s. We can consider the molecule to be composed of two oppositely charged point charges, H with a positive charge, and F with a negative charge. Calculate the potential difference between points 1 and 2, assuming the distances are much larger than the internuclear separation.
Example 3 Solution
Here we are asked to find the potential difference between two points on the axis of an electric dipole, as we can determine from the diagram. Since we are told that d>>s, we can approximate the magnitude of the electric field as [math]\displaystyle{ \vec{E}=\frac{1}{4\pi\epsilon_{0}}\frac{2p}{r^3} }[/math].
Therefore, we have:
[math]\displaystyle{ V_2 - V_1 = -\int_1^2 \frac{1}{4\pi\epsilon_{0}}\frac{2p}{x^3} dx = -\frac{1}{4\pi\epsilon_{0}}2p \int_1^2\frac{1}{x^3} dx }[/math]
where 1 and 2 are the distances d_1 and d_2 respectively. Integrating, we obtain:
[math]\displaystyle{ \frac {p}{4\pi\epsilon_{0}}(\frac{1}{d_{2}^2}-\frac{1}{d_{1}^2}) }[/math].
We know that p is equivalent to [math]\displaystyle{ \rho s }[/math], so our final answer is [math]\displaystyle{ V_2 - V_1 = \frac{\rho s}{4\pi\epsilon_{0}}(\frac{1}{d_{2}^2}-\frac{1}{d_{1}^2}) }[/math].
EXAMPLE 4: Electric Field Magnitude and Direction
What is the magnitude and direction of the electric field 1 cm above a 24e-6 C charge?
Answer: [math]\displaystyle{ E = ( \frac{1}{4\pi\varepsilon_0} )*(\frac{Q}{r^2}) }[/math]
[math]\displaystyle{ E = ( \frac{9e9*24e-6}{.01^2} ) }[/math]
= 2.16e9 N/C
EXAMPLE 5: Electric Field and Force
What is the electric field 1 mm away from a 38e-6 C charge? If a 2e-6 charge is placed in this field at this distance, what will the force be on it?
Answer:
[math]\displaystyle{ E = ( \frac{1}{4\pi\varepsilon_0} )*(\frac{Q}{r^2}) }[/math]
[math]\displaystyle{ E = ( \frac{9e9*38e-6}{.001^2} ) }[/math]
= 3.42e11 N/C
F = qE = 2e-6 * 3.42e11 N
EXAMPLE 6: Electron Traveling with Velocity
An electron is traveling at 1.8e6 m/s when it enters an electric field that slows it down. The field has a magnitude of 6200 N/C. How far does the electron go in the field before it stops?
Answer:
[math]\displaystyle{ KE = ( \frac{1}{2} ) * mv^2 }[/math]
[math]\displaystyle{ = ( \frac{1}{2} \right ) * 9.11e-31*1.8e6^2 }[/math]
= 1.476e-18 J
[math]\displaystyle{ F = qE = 1.6e-19 * 6200 = 9.92e-16 N }[/math]
[math]\displaystyle{ d = ( \frac{work}{F}) }[/math]
[math]\displaystyle{ d = ( \frac{1.476e-18}{9.92e-16} ) }[/math]
d = .0015 m
Connectedness
The abstract topics of electric field and electric potential are fascinating because they give physicists vast insight into the systems they are researching. Modeling the electric fields and electric forces of objects gives a more in-depth understanding of the underlying mechanics of the system, thus enabling scientists to better model the motion of the system and understand the energy that the system gains or loses. I find this topic quite interesting because we experience electric forces and electric fields everyday, and I never really understood the depth of that topic until I took this course. The relativity it has to everyday life is intriguing and worth learning about in my opinion.
Although the use of electric fields in Industrial Engineering is not too common, electric fields are used quite widely in other types of Engineering such as Biomedical Engineering, which sometimes has similar concepts to Industrial Engineering. Electric fields are used heavily in tissue engineering for measuring the properties of cells and tissues. The usage of electric fields concentrates mainly on the assembly of artificial tissues from its component cells. As a former Biomedical Engineering major, I find that very interesting; a physics discovery made centuries ago is still helpful in progressing the world of science and biomedicine today.
Today, we are able to see many interesting industrial applications of electric field and electric potential. One such application is the use of induced electric fields in the separation process of chromatography, which is used to draw compounds out of a mixture by capitalizing on their polarity, solubility, and with the use of electric fields, charge and magnetic affinity. Another application of electric fields is the removal of water by electroosmosis, which is a method that dates back to 1809 but has recently become useful for large-scale industrial operations.
Another great application of electric fields is in tissue engineering. This is done by assembling artificial tissues from their component cells using electrokinetics by assisting in the formation of the artificial extracellular matrix or by manipulating the cells themselves. There is also research on the effect on the biology of the cells when using electric fields.
History

In the early to mid 18th century, scores of scientists performed countless experiments where they passed electric currents through metal objects and tried to observe the effects that it had. It wasn't until 1831 that the relationship between electric field, potential and magnetism was determined by Michael Faraday, which is summed up in his principle of electromagnetic induction.
What Faraday discovered in 1831 by performing a series of experiments was that a changing magnetic field induced a current. His experiment consisted of wrapping two insulated coils of wire around an iron ring. The experiment showed that when a current is passed through one coil, another current is induced momentarily in the other coil. (this is now known as mutual induction, you can see the iron ring-coil at the Royal Institution if you're interested). In his next experiments, he moved a magnet through a loop of wire and found that an electric current flowed in that wire as well. He proved that a current even flowed if the loop was moving or over a non-moving magnet. Joseph Henry discovered the same thing, independently, a year later. Faraday explained electromagnetic induction (what this phenomena was soon named) using what he called "lines of force". At the time, most scientists rejected his theory because he could not back it up with mathematical equations. It wasn't until James Maxwell modeled his findings with math, known today as Faraday's Law, that scientists accepted his findings. These experiments, along with a few others, demonstrated that a changing magnetic field produced an electric field. Faraday's famous discovery was truly a breakthrough in science back then, and it continues to be very useful in the enhancement of science today. Since Faraday's experiment and Maxwell's mathematical model, these equations have changed slightly and people have used them to discover more great things in physics.
See also
For more information on Electric Field and Electric Potential or related topics, more resources are available to explore below.
Further Reading
Chabay, Ruth W., and Bruce A. Sherwood. Matter and Interactions: Electric and Magnetic Interactions. 4th ed. Vol. II. Place of Publication Not Identified: John Wiley, 2015. Print. Chapter 16. Section 16.5.
"Electric Field Applications: In Chromatography, Industrial and Chemical Processes." Electric Field Applications: In Chromatography, Industrial and Chemical Processes - Wiley Online Library. N.p., n.d. Web.
External links
Chemical Potential and Gibbs Distribution
Electric Field and Electric Potential
Electric Fields in Tissue Engineering
References
Georgia Institute of Technology. PHYS 2212. Intro Physics II. Lecture Notes. Darnton, Nicholas; Greco, Edwin.
Matter and Interactions. Vol II: Electric and Magnetic Interactions. Ruth W. Chabay. Bruce A. Sherwood.
https://www.khanacademy.org/test-prep/mcat/physical-processes/electrostatics-1/a/electric-potential
http://hyperphysics.phy-astr.gsu.edu/hbase/electric/efromv.html