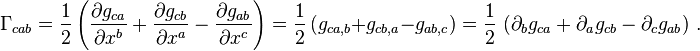Einstein's Theory of General Relativity

(Created by William Xia)

Einstein's Theory of General Relativity described gravity in the most detailed and accurate way that has ever been described. Multiple observations of the theory has been tested and experimentally verified, and new predictions have been observed through solving the equations in this theory.

The Main Idea

Gravity is the result of energy and matter distorting spacetime. The reason why one follows a curved trajectory when encountering an object in space is because the trajectory follows a least energy path through spacetime. In other words, if the smallest distance between two points in a plane is a straight line, then the smallest distance between two points in spacetime is described by how the object bends spacetime.

Mathematical Framework

Einstein developed a generalized coordinate system and summation notation to simplify his work and create a much more elegant system to describe his ideas. There are four important quantities to understand before tackling the Einstein Field Equations: metric tensor, christoffel symbols, geodesic equation, and the reimann tensor.

Metric Tensor

The metric tensor is a very important mathematical object in general relativity. Much of the information that describes a space is encoded in this object.

A tensor is a multidimensional quantity that describes direction and magnitude in a much more detailed way than a vector. For example, stress in an object is complex and contains many directions of forces at one single point, but by using a stress tensor one may compactly describe a point or even a collection of points. Writing equations in terms of tensors provides a very important quality: a tensor equation that equals zero in one frame of reference will equal zero in all frames of reference. This property provides a means for the study of physical phenomena in any system of coordinates imaginable.

The metric tensor is a subset of a tensor, in that the metric tensor is a generalization of the pythagorean theorem; a differential length is described by the metric tensor using generalized differential coordinates.

A basic example of the metric tensor is the Schwarzschild metric, which was one of the first metrics to be solved from Einstein's equations. The metric describes a simple sphere in spacetime, but despite the relative simplicity of the metric, it presents an interesting topic to study. By using the Schwarzschild metric, one may arrive at singularities, or mathematical points that explode to infinity. At these singularities, black holes are created, and these such points are still the subject of intense research.

Christoffel Symbols

Christoffel symbols can be loosely thought of as a residual when taking the derivative in a nonlinear coordinate system. If the coordinate system itself depends on a set of parameters, then taking the derivative of a function will not result in a simple derivative. Because of the product rule, there remains a correction term that must be required, and such term is the christoffel symbol. With respect to the metric tensor, the christoffel symbol has a concrete description of the tensor, and represents the correction quantity that must be used to describe geodesics, or shortest paths.

Geodesic Equation

The geodesic equation describes the path a particle takes in a general coordinate system, and it is a generalization of acceleration equations. For flat space, or simple cartesian coordinates, if a particle moves then it must move in a straight line disregarding any external forces, and indeed the geodesic equation resembles newton's second law. However, for curved space, say for example a sphere, the shortest path between to points is actually curved. When massive objects distort spacetime, the geodesic equation is helpful in describing paths particles must take in the distorted coordinate frame. Within the mathematical framework, the geodesic equation employs the christoffel symbol to correct for distortions in spacetime.

Reimann Tensor

Although the geodesic equation can describe motion in curved spacetime, the equation itself is insufficient in describing space. For such a description, one must turn to the Reimann Curvature Tensor. This tensor is one of the most common objects used to describe curved manifolds, and it plays a very important role in the Einstein Field Equations. The Einstein tensor itself contains a derivation of the reimann tensor, the ricci curvature tensor, and is what results from energy and mass tensor quantities.

The tensor is constructed by taking covariant derivatives of the metric, but it can also be rewritten in terms of the christoffel symbol.

An important idea that can be taken from the Reimann Tensor is parallel transport. Imagine one is on a hill and facing one direction. Move a certain distance, then move in another path, but this time, remain perpendicular to the surface. Repeat the movement until one ends up in the same point one started at. If one is facing a different direction than when one initially started, then there exists curvature inherent in the manifold. Parallel transport provides an effective means through which to describe the curvature of spacetime.

Experimental Verifications

Orbit of Mercury

In a classical two-body system, one object orbits another in a predictable manner. However, the observation of Mercury's orbit demonstrated a precession, which can be visualized as the orbit itself rotating around the Sun. It was only until Einstein introduced his theory that the precession was accurately accounted for.

Gravitational Lensing

When light passes through an object, it follows the geodesic trajectory described by Einstein's equations, and as a result bends. The first confirmation of gravitational lensing of light resulted from the measurement of a star's location during a solar eclipse. On May 1919 Arthur Eddington and his team observed stars near the sun and concluded that Einstein's predictions were consistent with empirical results.

Gravitational Redshift

The effect was only accurately measured in 1959 with the Pound-Rebka Experiment.

Connectedness

How is this topic connected to something that you are interested in?

I have always been fascinated by how gravity can be described in a rigorous mathematical sense, and the revolutionary nature of Einstein's work.

How is it connected to your major?

Electrical Engineers, when designing satellites, have to take into account the effects of GR in order to produce accurate time measurements. Recent experiments have also sought to measure minuscule changes in length and time due to gravitational waves and high velocities.

Is there an interesting industrial application?

For now, GR is restricted to mostly space applications. Away from the Earth's gravity, residents or machines orbiting the earth or traveling through space experience different effects on time and space due to fluctuating gravitational fields.

History

Einstein spent nearly 10 years refining his theory, from 1907 to 1915. After he published his results on Special Relativity, Einstein wanted to incorporate gravity into his theory, but did not realize how to do so until he stumbled upon differential geometric methods.

When the theory was first introduced, the empirical evidence for the theory did not exist, and many scientists around the world were eager to test Einstein's theories. Because of the counter-intuitive nature of Einstein's works, many doubted the validity of the theory, but with the the verification of the precession of mercury and gravitational lensing phenomena, relativity was all but confirmed.

References

Einstein, Albert. Relativity: The Special and General Theory. Methuen & Co Ltd, 1916. Print.

Pound, R. V.; Rebka, Jr. G. A. (November 1, 1959). "Gravitational Red-Shift in Nuclear Resonance". Physical Review Letters 3 (9): 439–441.

Rosenthal-Schneider, Ilse: Reality and Scientific Truth. Detroit: Wayne State University Press, 1980. p 74