Derivation of Average Velocity: Difference between revisions
Jump to navigation
Jump to search
mNo edit summary |
No edit summary |
||
| (12 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
Claimed by Gahan Wang (Fall 2016) | Claimed by Gahan Wang (Fall 2016) | ||
:The basic formula for average velocity is easy to understand, but how exactly can you prove this formula? This reference aims to show how using derivation through geometric, algebraic, and computer models proves the formula for average velocity. | |||
==The Main Idea== | ==The Main Idea== | ||
The main idea is to provide proof of the universal equation for average velocity. | The main idea is to provide proof of the universal equation for average velocity using derivation. The purpose is also to validate the derivation with fundamental concepts in science and in math. | ||
===A Mathematical Model=== | ===A Mathematical Model=== | ||
:T=Time | :<math> T </math> = Time | ||
: | :<math> p </math> = Momentum | ||
'''Geometric Derivation''' | '''Geometric Derivation''' | ||
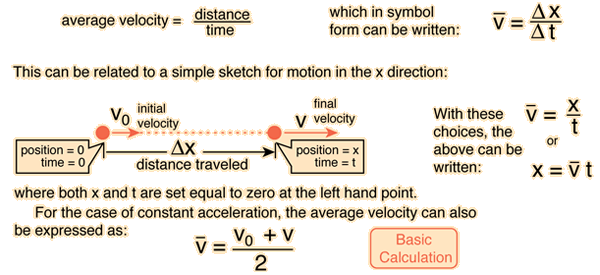
:The equation for average velocity is | :The equation for average velocity is <math> v_{avg} = {\frac{v_{ix} + v_{fx}}{2}} </math> when velocity in any direction is changing at a constant rate. | ||
When using geometry as proof, the area of a trapezoid can be used to support the derivation of average velocity. | :When using geometry as proof, the area of a trapezoid can be used to support the derivation of average velocity. <math> A_{trap} = {\frac{top + bottom}{2}} * altitude = x_f - x_i = {\frac{v_{ix} + v_{fx}}{2}} * (T_f - T_i) </math> | ||
:By dividing the change in time, we get the widely recognized formula for average velocity, | :By dividing the change in time, we get the widely recognized formula for average velocity, <math> {\frac{\Delta x}{\Delta t}} = {\frac{v_{ix} + v_{fx}}{2}} </math> | ||
'''Algebraic Derivation''' | '''Algebraic Derivation''' | ||
: | :Change in momentum is <math> \Delta p = F_{net} * \Delta t </math> which is also equal to <math> F_{net} = {\frac{\Delta p}{\Delta t}} </math>. | ||
:When evaluating the change in momentum as time approaches zero, | :When evaluating the change in momentum as time approaches zero, <math> F_{net} </math> becomes constant. When the change in time with respect to momentum is 0, <math> p = p_i </math>. | ||
: | :<math> v_x = {\frac{dx}{dt}} = {\frac{F_{net}}{m}}t + v_{ix} </math> | ||
: | :<math> v_{avg} = {\frac{x_f - x_i}{t}} = {\frac{1}{2}}{\frac{F_{net}}{m}}t + v_{ix} = {\frac{1}{2}}(v_{fx} - v_{ix}) + v_{ix} </math> | ||
: | :<math> v_{fx} = v_x = {\frac{F_{net}}{m}}t + v_{ix} </math> | ||
: | :After simplifying, <math> v_{avg} = {\frac{v_{ix} + v_{fx}}{2}} </math> where <math> v_x </math> changes at a constant rate. | ||
:Another way to look at it is where you start from the formula, <math> \frac{v_f + v_i}{2} </math>, and do: | |||
:<math> v_{avg} = {\frac{\Delta x}{\Delta t}} = {\frac{1}{t_f-t_i}}\int_{t_i}^{t_f}v(t), dt </math>, where <math> v(t) = a(t - t_i) + v_0 </math> | |||
:Plugging in <math> v(t) </math> into the integral would result in: | |||
:<math> {\frac{1}{t_f-t_i}}\int_{t_i}^{t_f}a(t - t_i) + v_0, dt </math> | |||
:Integrating separately, | |||
:<math> \frac{1}{t_f-t_i} * \int a(t_f - t_i) + v_0 - \int a(t_i - t_i) </math> | |||
:<math>= \frac{1}{t_f-t_i} * \int v_0 + \int at_f - at_i - \int v_0 </math> | |||
:<math>= \frac{1}{t_f-t_i} * \int at_f - at_i </math> | |||
:<math>= \frac{1}{t_f-t_i} * \frac{at_f^2}{2} - \frac{at_i^2}{2} </math> | |||
:<math>= \frac{1}{t_f-t_i} * \frac{at_f^2at_i^2}{2}, (t_f^2-t_i^2) = (t_f-t_i)(t_f+t-i) </math> | |||
:<math>= \frac{1}{t_f-t_i} * \frac{a(t_f-t_i)(t_f+t_i)}{2} </math> | |||
:<math>= \frac{a(t_f+t_i)}{2}, a = \frac{v(t)}{t} </math> | |||
:<math>= \frac{v_f+v_i}{2} </math> | |||
:Solving the integral results in the original equation, <math> \frac{v_f + v_i}{2} </math> | |||
==Examples== | ==Examples== | ||
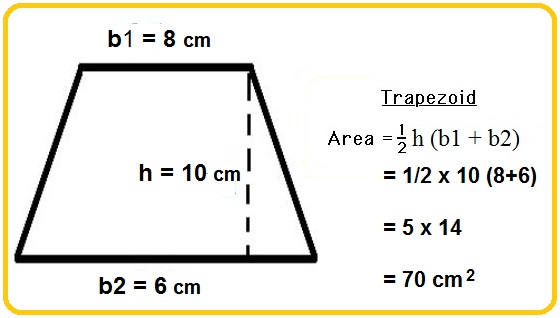
Geometric | '''Geometric Model Example''' | ||
[[File:TrapezoidExample.jpg]] | :[[File:TrapezoidExample.jpg]] | ||
*Area of the trapezoid = | *Area of the trapezoid = <math> x_{tot} </math> | ||
*Altitude = | *Altitude = <math> \Delta t </math> | ||
*Top side of trapezoid= | *Top side of trapezoid = <math> v_{xi} </math> | ||
*Bottom side of trapezoid= | *Bottom side of trapezoid = <math> v_{xf} </math> | ||
Algebraic | '''Algebraic Model Example''' | ||
:[[File:Avgvelocity.gif]] | |||
==Connectedness== | ==Connectedness== | ||
:Using basic, fundamental mathematical variables to prove physics equations shows the connection between math and science and how the same concept of limits and derivatives applies to an important, primary scientific principle in average velocity. | :Using basic, fundamental mathematical variables to prove physics equations shows the connection between math and science and how the same concept of limits and derivatives applies to an important, primary scientific principle in average velocity. One could also use Computer Science to create a program that could derive the average velocity formula. | ||
===Further Reading=== | |||
:https://www.youtube.com/watch?v=T_RjQAInWBc | |||
:https://www.boundless.com/physics/textbooks/boundless-physics-textbook/kinematics-2/speed-and-velocity-36/average-velocity-a-graphical-interpretation-210-6244/ | |||
===External links=== | ===External links=== | ||
| Line 52: | Line 74: | ||
:http://www.physicsclassroom.com/class/1DKin/Lesson-1/Speed-and-Velocity | :http://www.physicsclassroom.com/class/1DKin/Lesson-1/Speed-and-Velocity | ||
:http://hyperphysics.phy-astr.gsu.edu/hbase/mot.html | :http://hyperphysics.phy-astr.gsu.edu/hbase/mot.html | ||
http://www.luc.edu/faculty/dslavsk/courses/ntsc395/classnotes/ntsc395equations.pdf | |||
==References== | ==References== | ||
| Line 59: | Line 82: | ||
:Description of Motion. N.p., n.d. Web. 5 Dec. 2015. | :Description of Motion. N.p., n.d. Web. 5 Dec. 2015. | ||
:"Speed and Velocity." Speed and Velocity. The Physics Classroom, n.d. Web. 05 Dec. 2015. | :"Speed and Velocity." Speed and Velocity. The Physics Classroom, n.d. Web. 05 Dec. 2015. | ||
:"Derivation Of The Average Velocity Formula With Constant Acceleration (Using Calculus)". Physics.stackexchange.com. N.p., 2016. Web. 27 Nov. 2016. | |||
Latest revision as of 17:35, 8 August 2019
Claimed by Gahan Wang (Fall 2016)
- The basic formula for average velocity is easy to understand, but how exactly can you prove this formula? This reference aims to show how using derivation through geometric, algebraic, and computer models proves the formula for average velocity.
The Main Idea
The main idea is to provide proof of the universal equation for average velocity using derivation. The purpose is also to validate the derivation with fundamental concepts in science and in math.
A Mathematical Model
- [math]\displaystyle{ T }[/math] = Time
- [math]\displaystyle{ p }[/math] = Momentum
Geometric Derivation
- The equation for average velocity is [math]\displaystyle{ v_{avg} = {\frac{v_{ix} + v_{fx}}{2}} }[/math] when velocity in any direction is changing at a constant rate.
- When using geometry as proof, the area of a trapezoid can be used to support the derivation of average velocity. [math]\displaystyle{ A_{trap} = {\frac{top + bottom}{2}} * altitude = x_f - x_i = {\frac{v_{ix} + v_{fx}}{2}} * (T_f - T_i) }[/math]
- By dividing the change in time, we get the widely recognized formula for average velocity, [math]\displaystyle{ {\frac{\Delta x}{\Delta t}} = {\frac{v_{ix} + v_{fx}}{2}} }[/math]
Algebraic Derivation
- Change in momentum is [math]\displaystyle{ \Delta p = F_{net} * \Delta t }[/math] which is also equal to [math]\displaystyle{ F_{net} = {\frac{\Delta p}{\Delta t}} }[/math].
- When evaluating the change in momentum as time approaches zero, [math]\displaystyle{ F_{net} }[/math] becomes constant. When the change in time with respect to momentum is 0, [math]\displaystyle{ p = p_i }[/math].
- [math]\displaystyle{ v_x = {\frac{dx}{dt}} = {\frac{F_{net}}{m}}t + v_{ix} }[/math]
- [math]\displaystyle{ v_{avg} = {\frac{x_f - x_i}{t}} = {\frac{1}{2}}{\frac{F_{net}}{m}}t + v_{ix} = {\frac{1}{2}}(v_{fx} - v_{ix}) + v_{ix} }[/math]
- [math]\displaystyle{ v_{fx} = v_x = {\frac{F_{net}}{m}}t + v_{ix} }[/math]
- After simplifying, [math]\displaystyle{ v_{avg} = {\frac{v_{ix} + v_{fx}}{2}} }[/math] where [math]\displaystyle{ v_x }[/math] changes at a constant rate.
- Another way to look at it is where you start from the formula, [math]\displaystyle{ \frac{v_f + v_i}{2} }[/math], and do:
- [math]\displaystyle{ v_{avg} = {\frac{\Delta x}{\Delta t}} = {\frac{1}{t_f-t_i}}\int_{t_i}^{t_f}v(t), dt }[/math], where [math]\displaystyle{ v(t) = a(t - t_i) + v_0 }[/math]
- Plugging in [math]\displaystyle{ v(t) }[/math] into the integral would result in:
- [math]\displaystyle{ {\frac{1}{t_f-t_i}}\int_{t_i}^{t_f}a(t - t_i) + v_0, dt }[/math]
- Integrating separately,
- [math]\displaystyle{ \frac{1}{t_f-t_i} * \int a(t_f - t_i) + v_0 - \int a(t_i - t_i) }[/math]
- [math]\displaystyle{ = \frac{1}{t_f-t_i} * \int v_0 + \int at_f - at_i - \int v_0 }[/math]
- [math]\displaystyle{ = \frac{1}{t_f-t_i} * \int at_f - at_i }[/math]
- [math]\displaystyle{ = \frac{1}{t_f-t_i} * \frac{at_f^2}{2} - \frac{at_i^2}{2} }[/math]
- [math]\displaystyle{ = \frac{1}{t_f-t_i} * \frac{at_f^2at_i^2}{2}, (t_f^2-t_i^2) = (t_f-t_i)(t_f+t-i) }[/math]
- [math]\displaystyle{ = \frac{1}{t_f-t_i} * \frac{a(t_f-t_i)(t_f+t_i)}{2} }[/math]
- [math]\displaystyle{ = \frac{a(t_f+t_i)}{2}, a = \frac{v(t)}{t} }[/math]
- [math]\displaystyle{ = \frac{v_f+v_i}{2} }[/math]
- Solving the integral results in the original equation, [math]\displaystyle{ \frac{v_f + v_i}{2} }[/math]
Examples
Geometric Model Example
- Area of the trapezoid = [math]\displaystyle{ x_{tot} }[/math]
- Altitude = [math]\displaystyle{ \Delta t }[/math]
- Top side of trapezoid = [math]\displaystyle{ v_{xi} }[/math]
- Bottom side of trapezoid = [math]\displaystyle{ v_{xf} }[/math]
Algebraic Model Example
Connectedness
- Using basic, fundamental mathematical variables to prove physics equations shows the connection between math and science and how the same concept of limits and derivatives applies to an important, primary scientific principle in average velocity. One could also use Computer Science to create a program that could derive the average velocity formula.
Further Reading
- https://www.youtube.com/watch?v=T_RjQAInWBc
- https://www.boundless.com/physics/textbooks/boundless-physics-textbook/kinematics-2/speed-and-velocity-36/average-velocity-a-graphical-interpretation-210-6244/
External links
- http://physics.tutorvista.com/motion/average-velocity.html
- http://www.mathopenref.com/trapezoidarea.html
- http://www.physicsclassroom.com/class/1DKin/Lesson-1/Speed-and-Velocity
- http://hyperphysics.phy-astr.gsu.edu/hbase/mot.html
http://www.luc.edu/faculty/dslavsk/courses/ntsc395/classnotes/ntsc395equations.pdf
References
- "Area of a Trapezoid. Definition and Formula - Math Open Reference." Area of a Trapezoid. Definition and Formula - Math Open Reference. Math Open Reference, n.d. Web. 05 Dec. 2015.
- "Average Velocity." Average Velocity. TutorVista, n.d. Web. 05 Dec. 2015.
- Description of Motion. N.p., n.d. Web. 5 Dec. 2015.
- "Speed and Velocity." Speed and Velocity. The Physics Classroom, n.d. Web. 05 Dec. 2015.
- "Derivation Of The Average Velocity Formula With Constant Acceleration (Using Calculus)". Physics.stackexchange.com. N.p., 2016. Web. 27 Nov. 2016.