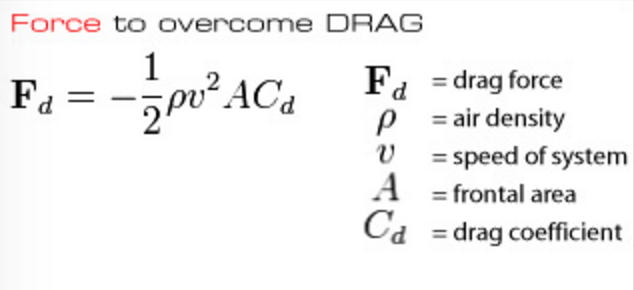Air Resistance

This page is in progress by Jayanth Chintham (jchintham3). 11/29/15

The Main Idea

The forces acting opposite to the direction of motion are called air resistance. Another term for this restraining effect is called "drag." Air resistance is an example of energy dissipation.

You may have noticed that moving objects quickly through any substance is harder than moving objects slowly through a substance. This is due to the air resistance. The magnitude of air resistance directly correlates to the speed of the object. Another aspect that impacts air resistance is the cross sectional area of a system. An example is a skydiver with an open parachute has more air resistance than a closed parachute. Air resistance force has an effect on the shape of an object as well. An example of this is a coffee filter, which is blunt object. A ball with the same cross sectional area as a coffee filter has less air resistance. The last effect that impacts air resistance is air density. An example is at higher altitudes (less air density) where there is less air resistance.

A Mathematical Model

The four factors that impact air resistance are cross sectional area, shape, air density, and speed. As you can see in the formula below, these four factors are included in the formula for the air resistance.

A Computational Model

[Air Resistance Using Glowscript][1]

Examples

Problem 1

You are standing at the top of a 20 building. You throw a ball in the horizontal direction with speed of 10 m/s. If you neglect air resistance, where would you expect the ball to hit on the plain surface below? Do you think your prediction without air resistance is too large or too small?

Solution:

height = (initial velocity in y direction)(time) + .5(acceleration from gravity)(time)^2

Since there is no initial velocity in the y direction, the equation is just:

height = .5(acceleration from gravity)(time)^2

20 = .5(9.8)(t)^2

Solve for t.

t = 2.02 seconds

range = (initial velocity in x direction)(time) + .5(acceleration in x direction)(time)^2

Since there is no acceleration in the x direction, the equation is just:

range = (initial velocity in x direction)(time)

range = (10)(2.02)

range = 20.2 meters

Our prediction without air resistance is too large, because air resistance has a force opposite to motion. This in turn would make the landing distance shorter.

Problem 2

John is going sky diving for the first time. His mass is 70 kg and his terminal speed is 38 m/s. What is the magnitude of the force of the air on John?

Solution:

At the terminal speed, the force of air (air resistance) is equal to the force of gravity.

Force air = Force gravity

Force air = (mass) (acceleration from gravity)

Force air = (70)(9.8)

Force air = 686 Newtons

Problem 3

Sarah is doing an air resistance experiment in class. The experiment requires Sarah to drop a coffee filter from a height of 2 meters. Let's say that the mass of the coffee filter was 2.0 grams, and it reached the ground with a speed of 1.0 m/s. How much kinetic energy did the air gain when Sarah dropped the coffee filter?

Solution:

Potential energy = (mass)(acceleration from gravity)(height)

Potential energy = (.002)(9.8)(2)

Potential energy = .0392 Joules

Kinetic Energy = .5(mass)(velocity)^2

Kinetic Energy = .5(.002)(1.0)^2

Kinetic Energy = .001 Joules

Total Energy = Potential Energy + Kinetic Energy

Total Energy = 0.0392 + 0.001 = 0.0402 Joules

Connectedness

1. How is this topic connected to something that you are interested in?
2. How is it connected to your major?
3. Is there an interesting industrial application?

History

Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.

See also

Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

Further reading

Books, Articles or other print media on this topic

External links

Internet resources on this topic

References

This section contains the the references you used while writing this page