Sound Barrier

Sound Barrier

Sound Barrier is a common term referring to the unusual amounts of drag in a fluid when an object approaches the speed of sound, which is about 1125 ft/s or 767 mph in dry air. First observed during World War II, the sound barrier doesn't exist as a physical limitation but rather represents the difficulty at which objects near the speed of sound experience when trying to accelerate further. The point at which the object does exceed this threshold, a shock wave is produced. The faster the object, the more conical the shock wave.

A common more easily understood example is that of a boat moving through water. The slow boat creates waves both behind and in front of it as the waves propagate faster than the boat can move. However once the boat starts moving faster than the waves can propagate, a wake is formed. Akin to the boat metaphor, an airplane moving through air creates sound waves and the resultant "wake" that is formed when moving supersonic speeds is called a sonic boom.

Shock Waves

These are regions of increased air pressure and temperature that are produced by any object moving through air and the most common example of a shock wave is the sonic boom.

Sonic Boom

The sonic boom is heard once the object passes the speed of sound. It is the result of all the compressible regions or high pressure regions in a wave front reaching the observer all at the same time instead of the usual delayed observed in the Doppler effect.

Overcoming Sound Barrier Limitations

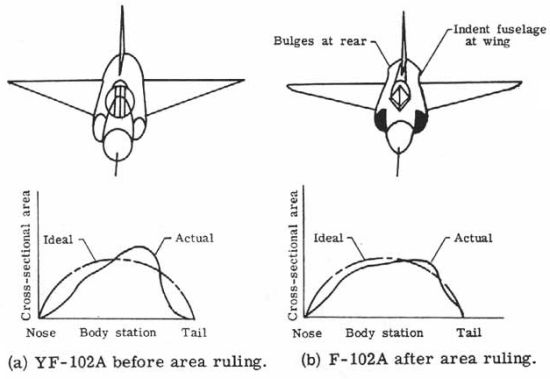
Area Rule

The Whitecomb Area rule (A.K.A transonic area rule) is an innovation in design to reduce the drag of an object at supersonic speeds created by Richard Whitecomb. It was created in attempts to limit the effects of the powerful and sudden drag objects experience when approaching the speed of sound. Relating both the longitudinal and latitude cross section of an object, usually an aircraft, the rule states.

1. Two airplanes with the same longitudinal cross sectional area have the same wave drag completely independent of how area is distributed laterally.
2. To avoid formation of strong shock waves (and thus a decrease in power) the total area distribution must be smooth.

As important as this rule is, it has recently been rendered relatively obsolete with the advent of newer and more powerful engines in airplanes which give the vehicle enough power to render the drag a small factor.

Connectedness

1. The Sound Barrier is a common problem that many commercial vehicles are trying to overcome. As a mechanical engineer, it is my hope that I would do work in improving the efficiency of airplanes and vehicles in moving in supersonic speeds.

History

Despite the relatively recent claim of breaking the sound barrier, it was broken long ago. The tip of a whip, when properly swung, actually breaks the sound barrier creating a shock wave that we hear as the audible crack. However, in terms of vehicles moving the speed of sound, it took much longer. Initial attempts to break the sound barrier often ended in failure due to the difficulty in controlling aircraft at supersonic speeds. While the barrier was often claimed to be broken when a vehicle entered a dive, most of these cases ended in the pilot crashing or were faulty. It wasn't until October 1947 in which Air Force pilot, Chuck Yeager, broke the sound barrier and reached mach .997, which has been argued to actually be a little above mach 1 but measurements were faulty.

See also

http://www.physicsbook.gatech.edu/Doppler_Effect

Further reading

Books, Articles or other print media on this topic

External links

Internet resources on this topic

References

http://science.howstuffworks.com/question73.htm http://www.physicscentral.com/explore/action/shockwaves.cfm http://www.physicsclassroom.com/class/sound/Lesson-3/The-Doppler-Effect-and-Shock-Waves https://en.wikipedia.org/wiki/Swept_wing https://en.wikipedia.org/wiki/Area_rule http://mathforum.org/library/drmath/view/56298.html