Velocity
Claimed by Stacey Nduati. edited by Christian Sewall
Velocity is the distance covered by an object in a specified direction over a time interval. In short, how fast something is moving, and what direction it is moving in. Velocity can be written as a vector, as it has both magnitude and direction. In contrast, speed only refers to how fast something is moving and has no direction.
Main Idea
Velocity is the vector measure of the rate that the position of an object is changing divided by the time that change in position takes. This measure can be used in tandem with ideas such as The Momentum Principle to predict such values as position, momentum, and velocity after a specified time interval.
A Mathematical Model
The primary way that velocity can be modeled is Average velocity can be calculated using the following equation:
- [math]\displaystyle{ \boldsymbol{\bar{v}} = \frac{\Delta\boldsymbol{r}}{\Delta\mathit{t}} }[/math] ,
where [math]\displaystyle{ {\Delta\boldsymbol{r}} }[/math] is the vector change of position of the object and [math]\displaystyle{ {\Delta\mathit{t}} }[/math] is the change of time.
[math]\displaystyle{ {\Delta\boldsymbol{r}} }[/math] can be found by subtracting the vector value of rfinal from the vector value of the original location, rinitial, to obtain a resultant vector that represents the displacement between the two positions over the given time interval
The SI units for velocity are meters per second (m/s).
A Computational Model
This model defines an object and models is displacement arbitrarily with its mass in relation to time,
m=9 g=9.81 t=0 deltat=1 positionInitial=vector(0,0,0) while t<6: positionFinal=vector(0,m*g*t,0) displacement=positionFinal-positionInitial velocity=displacement/deltat t=t+deltat print (velocity ,"is velocity")
Example
A car takes 3 hours to make a 230-mile trip from Point A to Point B.
| Hour 1 | Hour 2 | Hour 3 | |
|---|---|---|---|
| Velocity | 80 mph north | 90 mph north | 60 mph north |
There are two kinds of velocity in which one must consider: instantaneous velocity and average velocity. [1] does a good job explaining the difference between the two types of velocity
Instantaneous Velocity
Instantaneous velocity is the speed and direction of an object at a particular instant. Mathematically, it is the derivative of the position function at a specific point in time.
Given the example: Each hour, and each time point in every hour has a different instantaneous velocity.
Average Velocity
Average velocity is the net displacement of an object, divided by the total travel time. It is the average of all instantaneous velocities. It is important to note that as [math]\displaystyle{ {\Delta\mathit{t}} }[/math] gets very small, the average velocity approaches the instantaneous velocity.
Given the example: The average velocity would be (230 miles/3 hours) = 76.67 mph north.
Acceleration
Acceleration is the time rate of change of velocity, with the following equation:
- [math]\displaystyle{ \boldsymbol{a} = \frac{\Delta\boldsymbol{v}}{\Delta\mathit{t}} }[/math] ,
where [math]\displaystyle{ {\Delta\boldsymbol{v}} }[/math] is the change of velocity of the object and [math]\displaystyle{ {\Delta\mathit{t}} }[/math] is the change of time.
The SI units for acceleration are meters per second per second (m/s/s). It is also a vector quantity.
Given the example: The acceleration from the 1st hour to the 2nd hour is 10 mph. This indicates a positive acceleration. The acceleration from the 2nd hour to the 3rd hour is -30 mph. This indicates a negative acceleration.
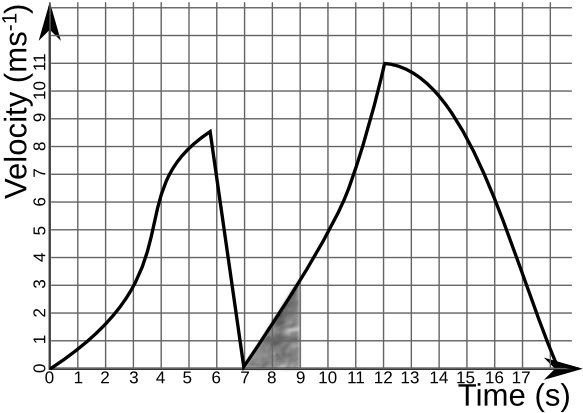
Another Example
Based on what you know about velocity in relation to acceleration. During the time interval of 3-5 seconds is the object accelerating or decelerating? How about from 12-14 seconds? How do you know both of these answers?
Given the Example: From 3-5 seconds, knowing that acceleration is the derivative of velocity, it can be seen that the object is accelerating, as the graph has a positive slopes.From 12-14 seconds, the graph has an increasingly negative slope, signifying deceleration towards zero.
Momentum
Another application of velocity is within the realm of momentum and the Momentum Principle. momentum is defined as the mass of an object multiple by its vector velocity quantity. Like velocity momentum is a vector quantity. This quantity can be used in conjunction with change in time to see the amount of force applied on an object, and by extension its final location and velocity. This can be modeled iteratively through computer programs or be done in one calculation.
A Final Example
If a van has a mass of 1200 kilograms, and it is traveling with a velocity of magnitude 38 m/s, what is its momentum?
Its momentum is 45,600 kg*m/s. This can be obtained by multiplying the mass by the magnitude of the velocity.
Connectedness
Velocity is a very simple yet interesting concept in the way that it can be applied to many different parts of physics from something as simple as displacement. Velocity's sheer versatility as a concept and the number of things that can be derived from it, which include acceleration, momentum, and by extension, force and mass. Also because it can be related to force, it can be used, in conjunction with other types of forces to determine many things about systems.
Velocity relates to my career aspirations in a rather interesting way. Because I plan on trying to become a trauma doctor, its easy to see the difference between high and low velocity impacts of objects of the same mass. If a low mass object is accelerating at a high enough velocity, the ramifications of its impact with the body could be vastly different than an object with a low velocity.
An industrial application of velocity could be seen in cars and the limits of their engines. The limit to which a car engine can perform can be tested in various ways, one of them being velocity. This could be one reason why you don't see normal cars with speed past around 130, the engine simply can't take it. The knowledge of the limit of a car engine can be tested using velocity to help ensure a safe driving experience for many.
See Also
References
1. Chabay, Ruth W., and Bruce A. Sherwood. Matter and Interactions. Hoboken, NJ: Wiley, 2011. Print.
2. "Velocity." Def. 2. Dictionary.com. N.p., n.d. Web. 29 Nov. 2015.
3. Velocity Expression. Digital image. Physics-Formulas. N.p., n.d. Web. 29 Nov. 2015.
4. Velocity vs Time Graph. Digital image. https://upload.wikimedia.org/wikipedia/commons/a/ae/Velocity-time_graph_example.png. N.p., n.d. Web. 29 Nov. 2015.