Vectors
Written by Elizabeth Robelo
Improved by Aparajita Satapathy
Improved by Lichao Tang
In physics, a vector is an object with a magnitude and a direction.
The Main Idea
A vector is an object with a magnitude and a direction. The magnitude of a vector is a scalar which represents the length of the vector. A vector is represented by an arrow. The orientation of the vector represents its direction. When a vector is drawn, the starting point is the tail and the ending point is called the head of the vector. Refer to the image below for a visual representation:

We can also add and subtract vectors. To add two vectors you align them head to tail and make sure that the tails of both vectors coincide with each other. The new added vector is the connecting arrow starting from the tail of one to the head of the other vector.
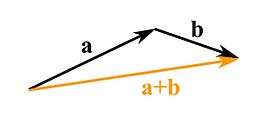
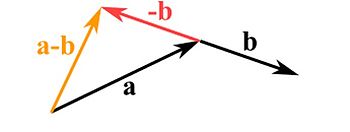
To subtract two vectors reverse the direction of the vector you want to subtract and continue to add them like shown before.
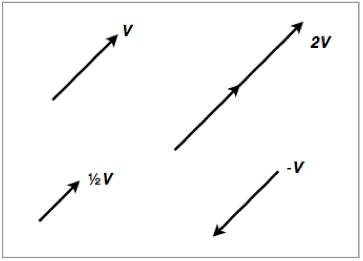
A vector can also be multiplied by a scalar. To multiply a vector by a scalar we can strech, compress or reverse the direction of a vector. If the scalar is between 0 and 1, the vector will be compresseed. If the scalar is greater than 1, the vector will get streched. If the scalar is a negative number, then the vector reverses its direction.
A Mathematical Model
Vectors are given by x, y, and z coordinates. They are written in the form <x, y, z> or (xi + yj - zk). Magnitude: [math]\displaystyle{ |A| = \sqrt{x^2 + y^2 + z^2} }[/math]
Dot Product: [math]\displaystyle{ \mathbf{A}\cdot\mathbf{B}=\sum_{i=1}^n A_iB_i=A_1B_1+A_2B_2+\cdots+A_nB_n }[/math]
Addition of two vectors: <a1, a2, a3> + <b1, b2, b3> = <a1 + b1, a2 + b2, a3 + b3>
Unit Vector: :[math]\displaystyle{ \mathbf{\hat{u}} = \frac{\mathbf{u}}{\|\mathbf{u}\|} }[/math]
Cross Product:a x b =ab*sin(theta)
Multiplication between vectors and scalars: c<a1, a2, a3> = <c*a1, c*a2, c*a3>
A Computational Model
In Physics 1, we have seen vectors in a computational model when we model it in vpython. Here is a sample code that creates a vector from a baseball to a tennis ball. Notice that the tail begins from the baseball and the head points to the tennis ball. vectors
Examples
Simple
Which of the following statements is correct?
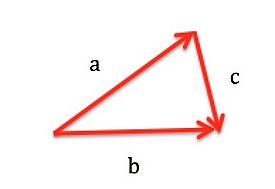
1. [math]\displaystyle{ \overrightarrow{c} = \overrightarrow{a} + \overrightarrow{b} }[/math]
2. [math]\displaystyle{ \overrightarrow{a} = \overrightarrow{b} - \overrightarrow{c} }[/math]
3. [math]\displaystyle{ \overrightarrow{a} = \overrightarrow{c} + \overrightarrow{b} }[/math]
4. [math]\displaystyle{ \overrightarrow{b} = \overrightarrow{c} + \overrightarrow{a} }[/math]
The answer is option number 2.
Middling
What is the magnitude of the vector C = A - B if A = <10, 5, 8> and B = <9, 4, 3>?
First we need to find the vector C: A - B = [math]\displaystyle{ \lt (10-9), (5-4), (8-3)\gt = \lt 1, 1, 5\gt = C }[/math]
[math]\displaystyle{ \sqrt{(1)^2 + 1^2 + 5^2} = 5.196 }[/math]
Difficult
What is the unit vector in the direction of the vector <10, 5, 8>? First you have to find the magnitude of the vector given: [math]\displaystyle{ \sqrt{10^2 + (5)^2 + 8^2} = 13.74 }[/math]
Finally divide the vector by its magnitude to get the unit vector:
[math]\displaystyle{ \tfrac{\lt 10, 5, 8\gt }{13.74} }[/math]
= <.727, .364, .582> Notice that the magnitude of the unit vector is equal to 1
Connectedness
1.Vectors will be used in many applications in physics. These can be two dimenstional or three dimensional vectors. Vectors are used to represent forces, fields and momentum.
2.Vectors has been used in many application problems in engineering majors. In engineering applications, vectors are used to a lot of quantities which have both magnitude and direction. For example in Biomedcial Engineering applications, vectors are used to represent the velocity of a flow to further calculate the flow rate and some other related quantities.
History
The discovery and use of vectors can date back to the ancient philosophers, Aristotle and Heron. The theory can also be found in the first article of Newtons Principia Mathematica. In the early 19th century Caspar Wessel, Jean Robert Argand, Carl Friedrich Gauss, and a few more depicted and worked with complex numbers as points on a 2D plane. in 1827, August Ferdinand published a book introducing line segments labelled with letters. he wrote about vectors without the name "vector".
In 1835, Giusto Bellavitis abstracted the basic idea of a vector while establishing the concept of equipollence. He called any pair of line segments of the same length and orientation equipollent (meaning equal length). He found a relationship and created the first set of vectors. Also in 1835 Hamilton founded "quaternions", which were 4D planes and equations with vectors.
William Rowan Hamilton devised the name "vector" as part of his system of quaternions consisting of three dimensional vectors.
Several other mathematicians developed similar vector systems to those of Bellavitis and Hamilton in the 19th century. The system used by Herman Grassman is the one that is most similar to the one used today.
See also
External links
Here is a link on more mathematical computations on vectors: [1]
Further Reading
Vector Analysis by Josiah Willard Gibbs