Polarization
Short Description of Topic Made By: tkapadia3 aka Tapas Kapadia
The Main Idea
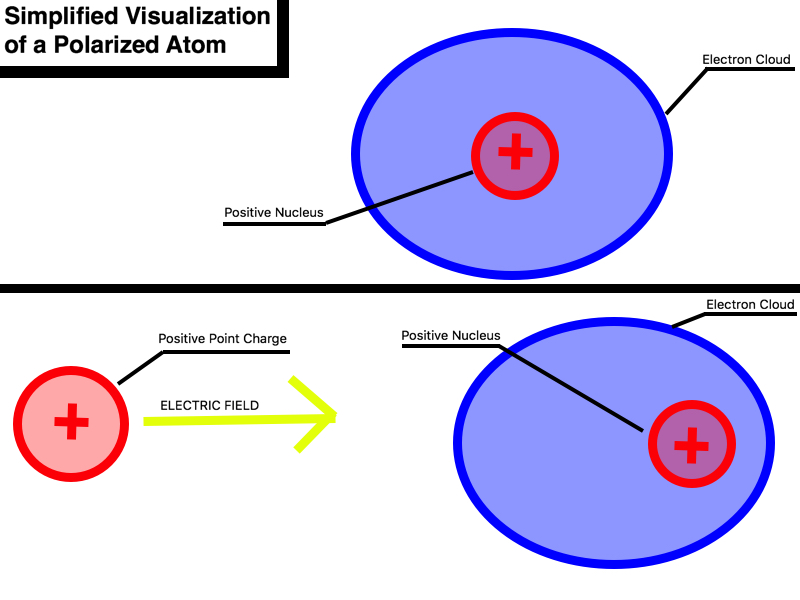
At an atomic level, external charges cause subatomic particles to restructure in way that is can be described as polarization. For example, a positive charge will create an outward field which will move the average electron position closer to the positive charge and the nucleus further away. Through this process of polarization, charges or electric fields effectively make neutral object induced dipoles. Polarization explains the attraction between charged objects and neutral object. A charged object creates an electric field that causes the opposite sign charge closer which in turn causes a net attraction. How readily a charged object can cause a material to polarize or the polarizability is different for different materials. The amount of polarization or the dipole moment is equal to the the polarizability multiplied by the electric field applied. The two main type of material are insulators and conductors and each of these handles polarization in a different way. It is important to understand that polarization itself does not induce charging. Polarization is the redistribution of charges throughout an object; a polarized neutral object is still a neutral object regardless of whether it is an insulator or conductor.
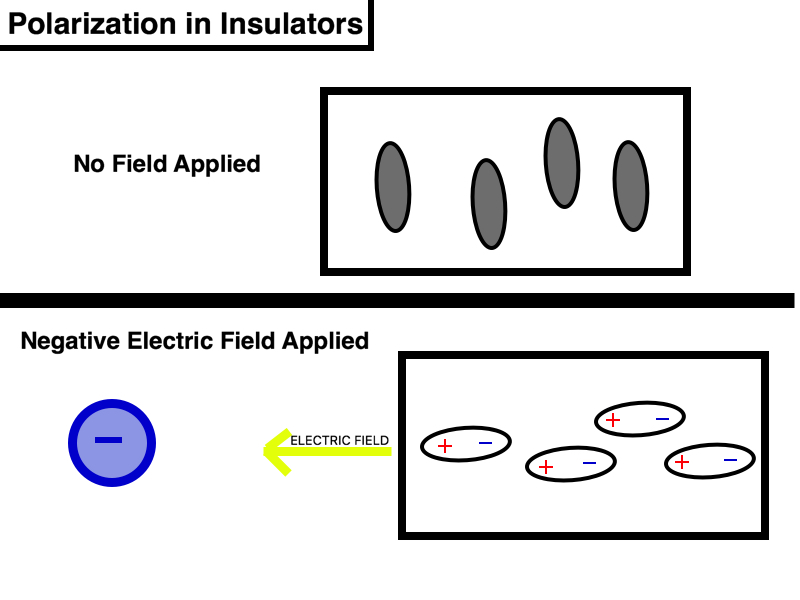
Polarization in Insulator: One main property of insulators is that electrons are tightly bound to the molecules. Therefore, there is no "sea of electrons" and the polarization happens much like what is shown below in which the actual atoms do not move very much but rather just reorient themselves to point correspondingly to the charges on or in the insulator. The net electric field is not equal to zero in the an insulator if there is a net electric field acting upon it.
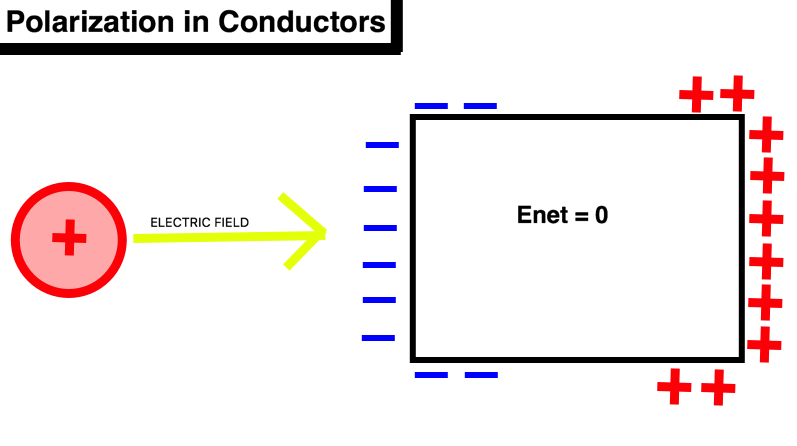
Polarization in Conductors: Polarization in conductors differs from polarization in insulators because conductors have charged particles that can move throughout the object. While insulators have atoms that simply reorient themselves, conductors have charged particles that can move distances due to external charges applied upon the material. The speed in which these mobile charges move due to an applied electric is known formally as drift speed. The drift speed is equal to the the net electric field at the location of the charge multiplied by a the mobility of the mobile charges. Another important property of conductors is that excess charges are always located out the outside on the surface of the conductor. Because the polarization causes the mobile charges to reorient on the surface, the net electric field always goes to zero. This state is known as equilibrium, and it features a electron drift speed equal to 0. The electric field of the polarization of the charges cancels out the electric field applied which which leaves no net electric field inside a conductor when it is at equilibrium.
A Mathematical Model
What are the mathematical equations that allow us to model polarization?
Electric Force: [math]\displaystyle{ \vec{F} = q\vec{E} }[/math] Where "F" is the electric force, "q" is the charge, and "E" is the electric field.
Dipole Moment: [math]\displaystyle{ \vec{P} = \alpha \vec{E} }[/math] Where "P" is the dipole moment, alpha is the polarizability (different for every material), and "E" is the applied electric field.
Drift Speed: [math]\displaystyle{ \vec{v} = \mu E_{net} }[/math] Where "v" is the drift speed, mu is the mobility of the charge, and "Enet" is the magnitude of the net electric field.
Examples
Simple
Determine if the statements below are True or False: 1. There are mobile charges conductors.
2. The net electric field is equal to 0 in both a conductor and insulator when at equilibrium.
3. Excess charge is located only the surface of insulators.
4. The average drift speed is of a mobile charge is proportional to the magnitude of the net electric field the material.
1 is true. There are mobile charges in conductor. It is insulators that do not have mobile charges. 2. False. The net electric field is 0 at equilibrium only in conductors. It is not the case in insulators. 3. False. The excess charges of conductors are located on the surface. In insulators, the excess charges are anywhere on or inside the material. 4. True. This is the formal for drift speed. [math]\displaystyle{ \vec{v} = \mu E_{net} }[/math]
Middling
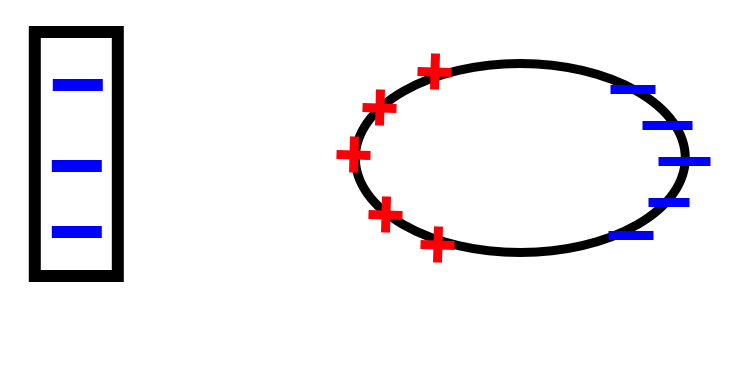
Does a negatively charged rod cause the metal sphere to polarize? If so, show the polarization of the neutral metal sphere, describe the electric field, and electric force caused by the negatively charged rod displayed below.

The electric field is toward the negatively charged rod. The electric force is pointed toward the charged as well. Thus the negative mobile charges are pushed to the surface of the far side of the sphere. The polarization essentially makes one giant dipole which has a net electric field of zero inside the sphere.
Difficult
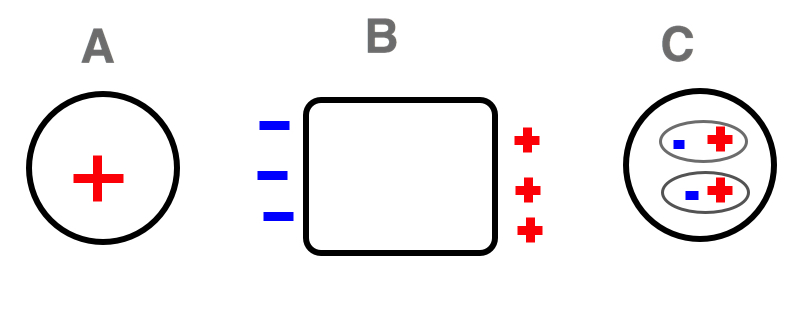
Find and show the polarization on Block B and Sphere C is Sphere A is plastic sphere with a positive charge. Block B is natural metal block while Sphere C is plastic sphere.
The positive charge of Sphere A creates a electric force which drives the positive mobile charges on away while attracting negative surface charges on the block. Due to this electric force the polarization on the block looks as it does below. The polarized block has positive surface charges near sphere C. Sphere C, however, is a conductor which means that there are no surface charges on Sphere C. In sphere C, a reorientation takes places. The negative ends orient close to the positive surface charges.
Connectedness
- How is this topic connected to something that you are interested in?
I have always been fascinated that something that is not charged could be attracted to something that is charged. Polarization explains this at a fundamental level which is something I find interesting. Learning how things at the the subatomic level is always fascinating for me.
- How is it connected to your major?
I am a computer engineering major. Honestly, I am not sure yet what Computer Engineering is all about. However, I am aware the polarization is an important concept in electrical engineering. Polarization of light waves seems to be more connected to my major.
- Is there an interesting industrial application?
The concept of polarization itself has many industrial applications. It is seen in 3D Glasses, Infrared spectroscopy, polarized sunglasses, FM radios, and even laptop screens. There are many, many industrial applications.
History
Polarization was discovered by Etienne Louis Malus. Etienne Louis Malus was a French physicist in the early 1800s who used concept that light is the range of electromagnetic radiation that humans cannot see to discover the concept we now know as polarization.
See also
Electric Field. Electric Force. Charge Density.
Further reading
Matter and Interactions Volume II.
External links
http://www.physicsclassroom.com/class/estatics/Lesson-1/Polarization
http://www.britannica.com/science/electric-polarization
https://www.youtube.com/watch?v=HKgOpmX-OFI
References
http://www.physicsclassroom.com/class/estatics/Lesson-1/Polarization
https://arago.elte.hu/sites/default/files/DSc-Thesis-2003-GaborHorvath-01.pdf
http://www.britannica.com/science/electric-polarization
http://www.innovateus.net/science/what-polarization
Matter and Interactions Volume II.
https://www.youtube.com/watch?v=HKgOpmX-OFI
http://www.physicsclassroom.com/class/light/Lesson-1/Polarization