2-Dimensional Motion
Kseniia Suleimanova Fall 2025
The Main Idea
When objects move in 2-dimensional space, their motion can be described in [math]\displaystyle{ \hat{x},\ \hat{y} }[/math] coordinates. The motion for each of those axes can be viewed independently. Another approach is using vectors (i.e. coordinate (5, 3) can be seen as vector [math]\displaystyle{ \langle 5,\ 3 \rangle }[/math]).
Displacement and distance
Imagine we have 2 points and origin O: A = [math]\displaystyle{ \langle a,\ b \rangle }[/math], B = [math]\displaystyle{ \langle c,\ d \rangle }[/math]
A point particle moves from origin to point A and then to point B. The displacement can be viewed as adding those vectors: [math]\displaystyle{ \langle a,\ b \rangle + \langle c,\ d \rangle = \langle a + c,\ b + d \rangle }[/math].
The distance is the sum of magnitudes of those vectors: [math]\displaystyle{ \sqrt{a^{2} + b^{2}} + \sqrt{c^{2} + d^{2}} }[/math]
Moving with a constant velocity
Velocity is the derivative of the position vector. In 2-dimensional space velocity looks the following: [math]\displaystyle{ \vec{v} = \frac{\Delta \vec{r}}{\Delta t} = \left\langle \frac{\Delta x}{\Delta t},\frac{\Delta y}{\Delta t} \right\rangle }[/math], so moving for [math]\displaystyle{ t }[/math] seconds with velocity [math]\displaystyle{ \vec{r} }[/math] can be represented as [math]\displaystyle{ \vec{v} \cdot t = \left\langle \frac{\Delta x}{\Delta t} \cdot t,\frac{\Delta y}{\Delta t} \cdot t \right\rangle }[/math]
Moving with constant acceleration
In 2-dimensional space acceleration is [math]\displaystyle{ \vec{a} = \frac{\Delta \vec{v}}{\Delta t}= \left\langle \frac{\Delta v_x}{\Delta t},\frac{\Delta v_y}{\Delta t} \right\rangle }[/math].
A standard formula for position update is still applicable for vectors in 2-dimensional space: [math]\displaystyle{ \vec{r}(t)=\vec{r}_0+\vec{v}_0 t+\tfrac{1}{2}\vec{a}\,t^{2}=\langle x_0+v_{0x}t+\tfrac{1}{2}a_x t^{2},\ y_0+v_{0y}t+\tfrac{1}{2}a_y t^{2}\rangle }[/math]
Computational models
Projectile motion
https://www.glowscript.org/#/user/ksuleimanova/folder/MyPrograms/program/projectilemotiondemo - link to execute the code
Web VPython 3.2
scene.range = 10
scene.center = vector(5, 5, 0)
r = vector(0, 10, 0)
v = vector(3, 2, 0)
a = vector(0, -9.8, 0)
dt = 0.05
ball = sphere(pos=r, radius=0.2, color=color.red, make_trail=True)
gx = graph(title="Projectile Motion",
xtitle="Time, s", ytitle="Position, m")
xplot = gcurve(color=color.blue, label="x(t)")
yplot = gcurve(color=color.green, label="y(t)")
t = 0
while r.y >= 0:
rate(100)
v = v + a * dt
r = r + v * dt
ball.pos = r
xplot.plot(t, r.x)
yplot.plot(t, r.y)
t = t + dt
In this code the position is updated every small increment of time, using the position update formula for constant acceleration, involving velocity first, and then position:
v = v + a * dt r = r + v * dt
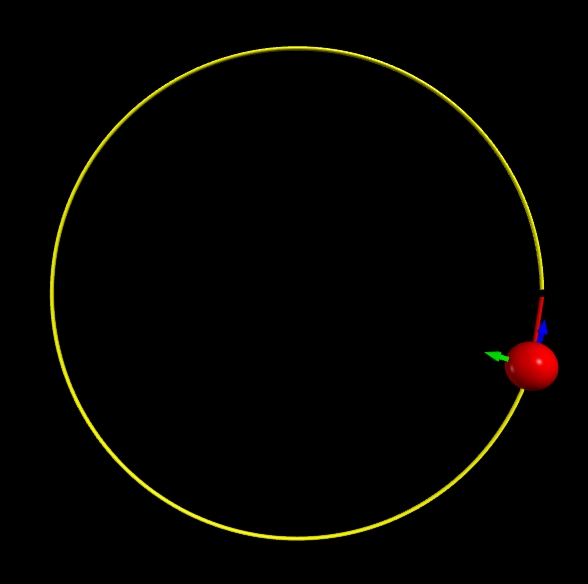
Circular motion
In the circular velocity magnitude is constant, while its direction changes.
https://www.glowscript.org/#/user/ksuleimanova/folder/MyPrograms/program/circularmotion - link to execute the code
Web VPython 3.2
scene.width = 600
scene.height = 600
R = 5
omega = 1
dt = 0.05
particle = sphere(pos=vector(R,0,0), radius=0.5, color=color.red, make_trail=True)
arrow_velocity = arrow(pos=particle.pos, axis=vector(0,1,0), color=color.blue, shaftwidth=0.1)
arrow_accel = arrow(pos=particle.pos, axis=vector(0,1,0), color=color.green, shaftwidth=0.1)
t = 0
v_mag = 3
velocity = vector(0, v_mag, 0)
path = curve(color=color.yellow)
while t < 10:
particle.pos = particle.pos + velocity*dt
accel = - (velocity.mag**2 / R) * particle.pos.norm()
velocity = velocity + accel*dt
arrow_velocity.pos = particle.pos
arrow_velocity.axis = velocity.norm()
arrow_accel.pos = particle.pos
arrow_accel.axis = accel.norm()
path.append(pos=particle.pos)
t += dt
Examples
Easy
Problem: A point particle starts at a point (0, 5)m on a flat surface an moves with a constant velocity [math]\displaystyle{ \langle 4,\ 1 \rangle m }[/math]. Find it's position after 5 seconds.
Solution: Intial position vector is [math]\displaystyle{ \langle 0,\ 5 \rangle m }[/math] As the velocity is constant, acceleration is 0. Insert all the data into the position update formula: [math]\displaystyle{ \vec{r}(t)=\vec{r}_0+\vec{v}_0 t+\tfrac{1}{2}\vec{a}\,t^{2}=\vec{r}_0+\vec{v}_0 t + 0 = \langle 0,\ 5 \rangle + \langle 4,\ 1 \rangle \cdot 5 = \langle 20,\ 10 \rangle m }[/math]
Medium
Problem: A bug on the table travels from point (1, 2)m to point (2, 1)m and then to (2, 2)m. The whole path takes 2 seconds. Find average speed and average velocity.
Solution: Displacement is [math]\displaystyle{ \langle 2,\ 2 \rangle - \langle 1,\ 2 \rangle = \langle 1,\ 0 \rangle m }[/math] Distance is the length of the path: [math]\displaystyle{ \sqrt{(2 - 1)^{2} + (1 - 2)^{2}} + \sqrt{(2 - 2)^{2} + (2 - 1)^{2}} = \sqrt{2} + \sqrt{1} = 2.41 m }[/math]
Average speed: [math]\displaystyle{ 2.41 / 2 = 1.21 m/s }[/math]
Average velocity: [math]\displaystyle{ \langle 1,\ 0 \rangle / 2 = \langle 0.5,\ 0 \rangle m/s }[/math]
Hard
Problem: The ball is thrown from the building with the height 10 meters. The initial velocity of the ball is [math]\displaystyle{ \langle 3,\ 2 \rangle \textit{m/s} }[/math] find the time and position when the ball reaches its maximum height.
Solution: This is the projectile motion problem in 2-dimensional space. The most convenient approach is to view vertical and horizontal motion independently. We know that horizontal component of the velocity stays the same, while [math]\displaystyle{ \vec{v}_{y} = \vec{v}_{y_{init}} - g t }[/math] - the ball moves with a constant acceleration. For the [math]\displaystyle{ \hat{y} }[/math] we can use the position update formula for constant acceleration [math]\displaystyle{ -g }[/math]: [math]\displaystyle{ r_{y}(t)=r_{y_0}+\vec{v_{y_0}} t-\tfrac{1}{2}\vec{g}\,t^{2} }[/math]. This is a parabola that has a maximum value. Insert numerical values and solve the equation: [math]\displaystyle{ r_{y}(t)=10+2 t-\tfrac{1}{2}\cdot 9.8 \cdot t^{2} }[/math]. Maximum value is achieved at [math]\displaystyle{ t = 0.21 s }[/math]. At [math]\displaystyle{ t_{max} = 0.21 s }[/math] x-coordinate is [math]\displaystyle{ r_{x_{init}} = \vec{v_x} \cdot t_{max} = 0 + 3 \cdot 0.21 = 0.63 m }[/math] y-coordinate is [math]\displaystyle{ r_{y}(0.21)=r_{y_0}+\vec{v_{y_0}} \cdot 0.21-\tfrac{1}{2}\vec{g} \cdot 0.21^{2} = 10 + 3 \cdot 0.21 - \tfrac{1}{2} \cdot 9.8 \cdot 0.21 = 10.41 m }[/math]
Links To Other Topics
- 2-dimensional motion relies on vectors most of the time
- Most projectile motion problems are 2-dimensional
- Centripital motion problems are 2-dimensional as well
See Also
https://youtu.be/w3BhzYI6zXU?si=oivAjOifOPBi_5D4 - vectors and 2D motion
https://youtu.be/On5DpeGQ89I?si=7zqYvWx73W3HYwjG - 2D motion problems with solutions