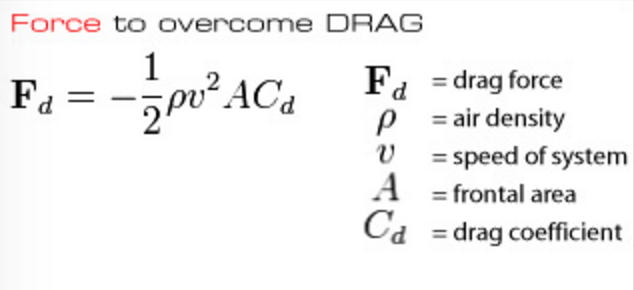Air Resistance

This page is in progress by Jayanth Chintham (jchintham3). 11/29/15

The Main Idea

The forces acting opposite to the direction of motion are called air resistance. Another term for this restraining effect is called "drag." Air resistance is an example of energy dissipation.

You may have noticed that moving objects quickly through any substance is harder than moving objects slowly through a substance. This is due to the air resistance. The magnitude of air resistance directly correlates to the speed of the object. Another aspect that impacts air resistance is the cross sectional area of a system. An example is a skydiver with an open parachute has more air resistance than a closed parachute. Air resistance force has an effect on the shape of an object as well. An example of this is a coffee filter, which is blunt object. A ball with the same cross sectional area as a coffee filter has less air resistance. The last effect that impacts air resistance is air density. An example is at higher altitudes (less air density) where there is less air resistance.

A Mathematical Model

The four factors that impact air resistance are cross sectional area, shape, air density, and speed. As you can see in the formula below, these four factors are included in the formula for the air resistance.

A Computational Model

[Air Resistance Using Glowscript][1]

Rotational Motion on Air Resistance

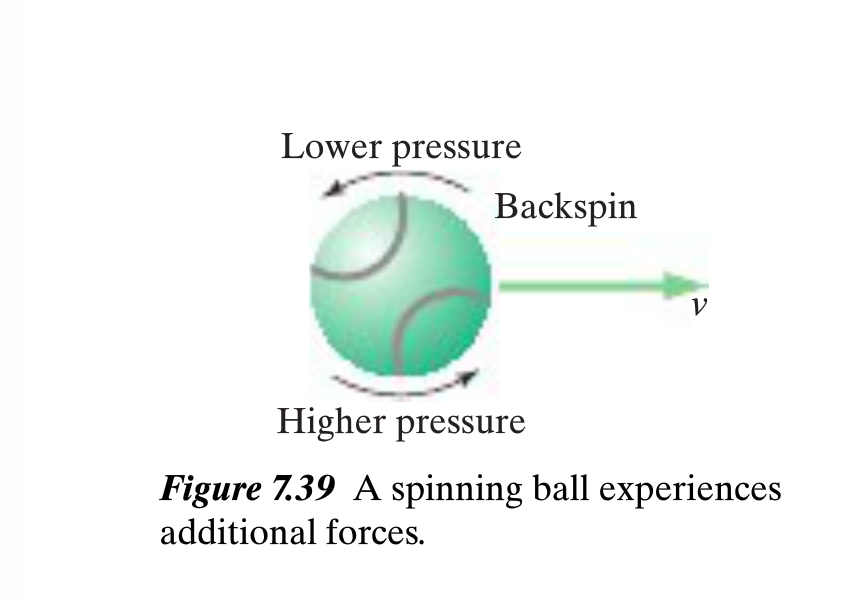
If a ball has spin, there is an effect of fluid flow around the ball that raises the air pressure on the side where the rotational motion is in the same direction as the ball's velocity, and lowers the air pressure on the other side, where the rotational motion is in the opposite direction to the velocity. In the figure above, the force points upward due to "backspin" and lifts the ball extending the range. In the case where there is topspin on the ball, the force is downward decreasing the range. This topic is related to fluid dynamics.

Examples

Problem 1

You are standing at the top of a 20 building. You throw a ball in the horizontal direction with speed of 10 m/s. If you neglect air resistance, where would you expect the ball to hit on the plain surface below? Do you think your prediction without air resistance is too large or too small?

Solution:

height = (initial velocity in y direction)(time) + .5(acceleration from gravity)(time)^2

Since there is no initial velocity in the y direction, the equation is just:

height = .5(acceleration from gravity)(time)^2

20 = .5(9.8)(t)^2

Solve for t.

t = 2.02 seconds

range = (initial velocity in x direction)(time) + .5(acceleration in x direction)(time)^2

Since there is no acceleration in the x direction, the equation is just:

range = (initial velocity in x direction)(time)

range = (10)(2.02)

range = 20.2 meters

Our prediction without air resistance is too large, because air resistance has a force opposite to motion. This in turn would make the landing distance shorter.

Problem 2

John is going sky diving for the first time. His mass is 70 kg and his terminal speed is 38 m/s. What is the magnitude of the force of the air on John?

Solution:

At the terminal speed, the force of air (air resistance) is equal to the force of gravity.

Force air = Force gravity

Force air = (mass) (acceleration from gravity)

Force air = (70)(9.8)

Force air = 686 Newtons

Problem 3

Sarah is doing an air resistance experiment in class. The experiment requires Sarah to drop a coffee filter from a height of 2 meters. Let's say that the mass of the coffee filter was 2.0 grams, and it reached the ground with a speed of 1.0 m/s. How much kinetic energy did the air gain when Sarah dropped the coffee filter?

Solution:

Potential energy = (mass)(acceleration from gravity)(height)

Potential energy = (.002)(9.8)(2)

Potential energy = .0392 Joules

Kinetic Energy = .5(mass)(velocity)^2

Kinetic Energy = .5(.002)(1.0)^2

Kinetic Energy = .001 Joules

Total Energy = Potential Energy + Kinetic Energy

Total Energy = 0.0392 + 0.001 = 0.0402 Joules

Connectedness

How is this topic connected to something that you are interested in?

As an adventurous person, I have always been interested in skydiving. Air resistance is a huge factor in skydiving, as it allows you to reach the ground safely just with a parachute. There are many factors in releasing a parachute to have the safest possible landing. When you release your parachute and how to control your parachute are very important in having a safe landing. Also, there is obviously a lot of air resistance in a parachute because of the large cross sectional area.

Another topic that air resistance plays a factor in is sports. A specific sport that air resistance impacts is tennis. Spin is very important in tennis, because it allows you to control where the ball lands. If there is topspin on a ball, the air resistance is less allowing the ball to come down faster. If there is backspin, the ball stays in the air longer being controlled by the air.

How is it connected to your major?

I am an aerospace engineer, so air resistance has a lot of application in my field. Especially in aircraft design and manufacturing, aerospace engineers must design a aircraft that allows for the least air resistance. This allows for more control over the plane.

Is there an interesting industrial application?

Air resistance has a lot of application in speed sports. Also, air resistance plays a big factor in skydiving and anything with a parachute. Lastly, the aircraft industry factors in air resistance into all of their products, as this force is very important in certain situations.

History

Aristotle was the first to write about air resistance in the 4th century BC. In the 15th century, Leonardo da Vinci published the Codex Leicester, in which he rejected Aristotle's theory and attempted to prove that the only effect of air on a thrown object was to resist its motion. The first equation for air resistance was:

This equation overestimates drag in most cases, and was often used in the 19th century to argue the impossibility of human flight.

Louis Charles Breguet's paper of 1922 began efforts to reduce drag by streamlining. A further major call for streamlining was made by Sir Melvill Jones who provided the theoretical concepts to demonstrate emphatically the importance of streamlining in aircraft design. The aspect of Jones’s paper that most shocked the designers of the time was his plot of the horse power required versus velocity, for an actual and an ideal plane.

Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.

See also

Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

Further reading

http://www.physicsclassroom.com/class/newtlaws/Lesson-3/Free-Fall-and-Air-Resistance[http://www.physicsclassroom.com/class/newtlaws/Lesson-3/Free-Fall-and-Air-Resistance

http://www.forbes.com/sites/chadorzel/2015/09/29/the-annoying-physics-of-air-resistance/[2]

External links

Internet resources on this topic

References

This section contains the the references you used while writing this page