Fourier Series and Transform: Difference between revisions
Jump to navigation
Jump to search
Created page with "A Fourier series is an expansion of trigonometric functions to model periodic functions. This method proves useful in the study of harmonic systems as the analysis in a more familiar domain is much simpler than in its original domain. It has a variety of applications ranging from signal processing to quantum mechanics. The Fourier Series is defined as <math>f(x)=\sum_{n=1}^{\infty}{a_n\cos{(\frac{nx}{L}})}+\sum_{n=1}^{\infty}{b_n\sin{(\frac{nx}{L}})}</math> ==Intuition==..." |
No edit summary |
||
| Line 1: | Line 1: | ||
A Fourier series is an expansion of trigonometric functions to model periodic functions. This method proves useful in the study of harmonic systems as the analysis in a more familiar domain is much simpler than in its original domain. It has a variety of applications ranging from signal processing to quantum mechanics. The Fourier Series is defined as <math>f(x)=\sum_{n=1}^{\infty}{a_n\cos{(\frac{nx}{L}})}+\sum_{n=1}^{\infty}{b_n\sin{(\frac{nx}{L}})}</math> | A Fourier series is an expansion of trigonometric functions to model periodic functions. This method proves useful in the study of harmonic systems as the analysis in a more familiar domain is much simpler than in its original domain. It has a variety of applications ranging from signal processing to quantum mechanics. The Fourier Series is defined as: <br><math>f(x)=\sum_{n=1}^{\infty}{a_n\cos{(\frac{nx}{L}})}+\sum_{n=1}^{\infty}{b_n\sin{(\frac{nx}{L}})}</math> | ||
==Intuition== | ==Intuition== | ||
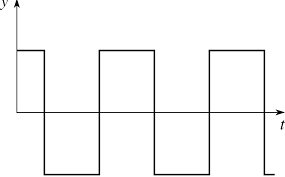
Many physical systems can be modeled by square waves. Consider systems with on-off behavior, similar to an on-and-off switch. A square wave looks like this: | Many physical systems can be modeled by square waves. Consider systems with on-off behavior, similar to an on-and-off switch. A square wave looks like this:<br> | ||
[[File:squarewave.png|500px|]] | |||
Revision as of 23:03, 5 December 2022
A Fourier series is an expansion of trigonometric functions to model periodic functions. This method proves useful in the study of harmonic systems as the analysis in a more familiar domain is much simpler than in its original domain. It has a variety of applications ranging from signal processing to quantum mechanics. The Fourier Series is defined as:
[math]\displaystyle{ f(x)=\sum_{n=1}^{\infty}{a_n\cos{(\frac{nx}{L}})}+\sum_{n=1}^{\infty}{b_n\sin{(\frac{nx}{L}})} }[/math]
Intuition
Many physical systems can be modeled by square waves. Consider systems with on-off behavior, similar to an on-and-off switch. A square wave looks like this: