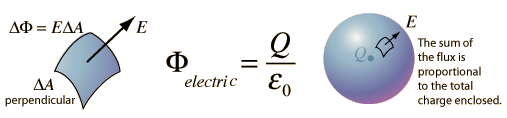Gauss's Law

Claimed by Charu Thomas (SPRING 2017) Claimed by Lin Htet Kyaw FALL 2017

Gauss's Law is an equation relating the charges and electric flux. It states that net electric flux outside a surface is equal to the charge inside the surface over the constant permittivity of space (ε0 = 8.854187817...×10−12 F⋅m−1). Coulomb's Law and Gauss's Law are intimately connected because Coulomb's Law relates the charge to electric field. Gauss's Law relates electric flux, a quantity that is equal to the product of the perpendicular component of E-field and Area of closed surface. It is one of Maxwell's Equations, formulated by Carl Friedrich Gauss, a notorious German mathematician.

The Main Idea

We know from the previous introduction of flux that there is a relationship between the electric flux on a closed surface and the charges inside the surface. However, we would like to figure out what that particular factor is.

We start by considering a point charge of +Q enclosed by an imaginary spherical shell.

Everywhere on the imaginary shell, the electric field produced is parallel to the normal unit vector. Cos(0) = 1, so the dot product evaluates to the magnitude of the electric field. Recall that the surface area of the imaginary sphere is 4*pi*r^2. With Coulomb's Law and the surface area of a sphere, we get that electric flux is equal to +Q/ε0. This implies that the factor is 1/ε0.

Note that if the point charge was negative, the electric field would still be parallel, just opposite direction. Cos(180) = -1 so the dot product would be -1 times the magnitude of the electric field.

To summarize, the idea of Gauss's Law is that the electric flux out of a closed surface is equivalent to the charge enclosed, divided by the permittivity.

A Mathematical Model

A very helpful and clear summary of this Law can be found in the diagram below. As can be seen on the left side of this diagram, change in flux equals electric field multiplied by change in area.

Image Taken from Hyperphysics

To more clearly state it, the formula for this Law is the electric flux equals the total charge contained by a closed surface, divided by the permittivity (epsilon naught: ε0 = 8.854187817...×10−12 F⋅m−1).

The picture below illustrates Gauss's Law with a detailed explanation.

Examples

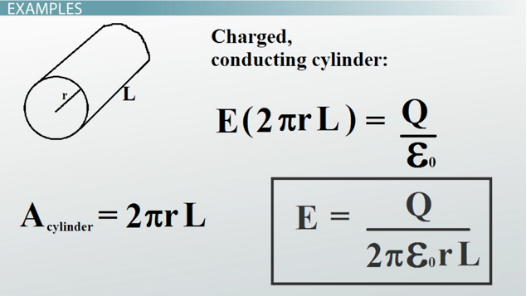
Example 1: In order to apply Gauss's Law, it is important to be certain you are working with a closed surface, then set electric flux equal to the internal field divided by the permittivity (epsilon naught: ε0 = 8.854187817...×10−12 F⋅m−1). An example of this Law being applied can be found below.

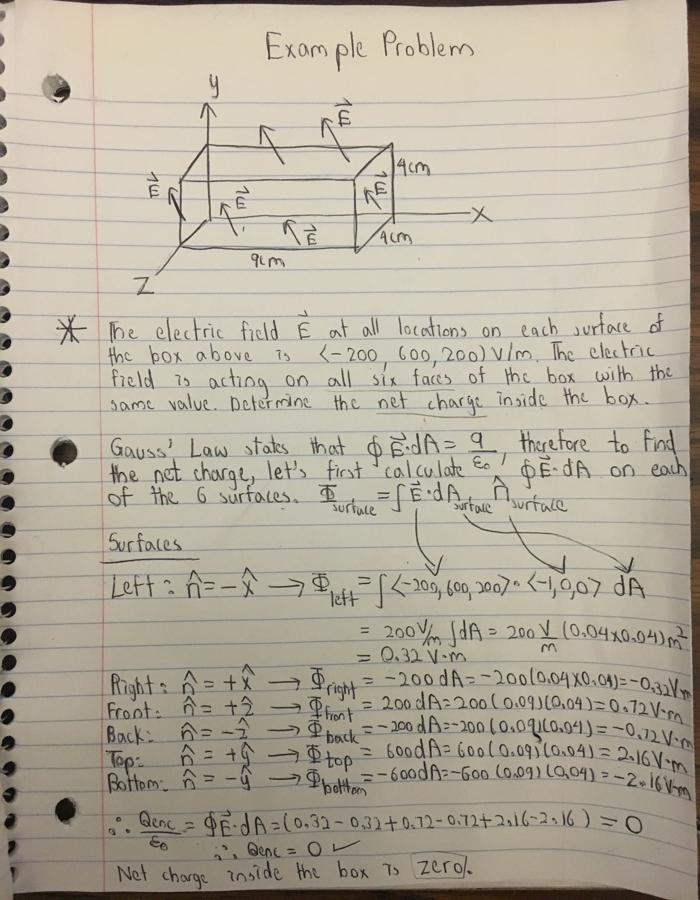
Example 2: The example below shows how to calculate the net charge enclosed by a box.

Example 3: The example below shows how to determine the net charge located inside a box and is fundamental to understanding Gauss's Law. It demonstrates the idea that to calculate the net charge inside a box, we have to start off by calculating the fluxes acting on all surfaces on the box using none other than the Gauss's Law.

Connectedness

Gauss's Law, as well as the other Maxwell Equations form a basis for electrodynamics. They are the fundamental core of this field of study. Magnetostatics study is also closely related to Gauss's Law, but in particular Gauss's Law of Magnetism, which is very similar to Gauss's Law relating to electric fields.

As Industrial and Systems Engineering majors, we deal with many statistical distributions. A very important fundamental distribution is the Gaussian distribution or the Normal Distribution. With inference, the Gaussian Distribution comes up in confidence intervals for single statistics. With comparison inference, like finding the pairwise difference between statistics, generally we use other distributions such as the T-Distribution. However, the T-Distribution approximates the Gaussian distribution with degrees of freedom greater than 29.

History

Carl Friedrich Gauss was a German Mathematician and Physicist who contributed notably to a wide variety of fields regarding mathematical and scientific study. He has been referred to as the "greatest mathematician since antiquity" and the "foremost of mathematicians". He is considered one of the most impactful and influential contributors to the fields of Mathematics and Physics in history.

See also

Gauss's Law is tied in closely with the other of Maxwell's equations that can be found here in the Physics Book.

http://physicsbook.gatech.edu/Gauss%27s_Flux_Theorem

http://physicsbook.gatech.edu/Faraday%27s_Law

http://physicsbook.gatech.edu/Magnetic_Flux

http://physicsbook.gatech.edu/Ampere%27s_Law

External links

http://physics.info/law-gauss/

https://en.wikipedia.org/wiki/Gauss%27s_law

https://en.wikipedia.org/wiki/Carl_Friedrich_Gauss

References

http://hyperphysics.phy-astr.gsu.edu/hbase/electric/gaulaw.html

https://web.iit.edu/sites/web/files/departments/academic-affairs/academic-resource-center/pdfs/Gauss_Law.pdf

spiff.rit.edu

study.com