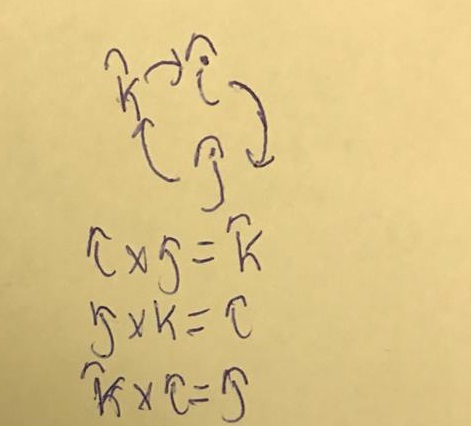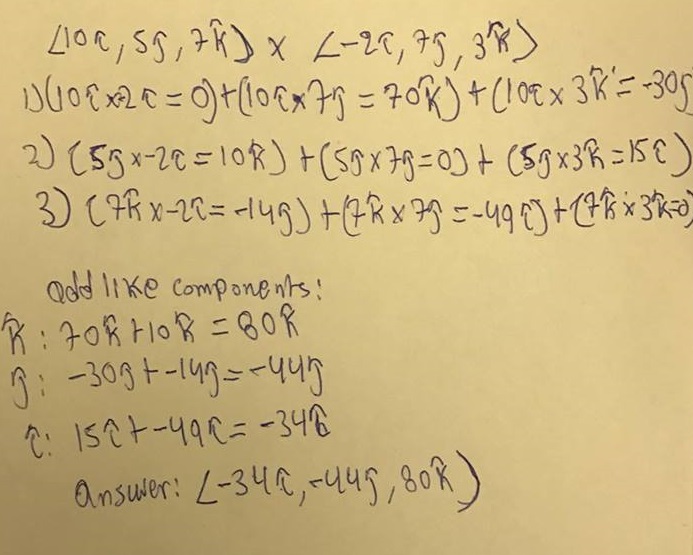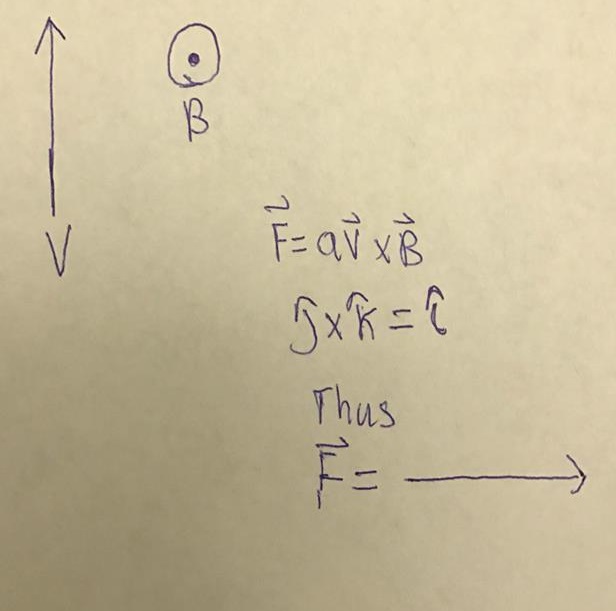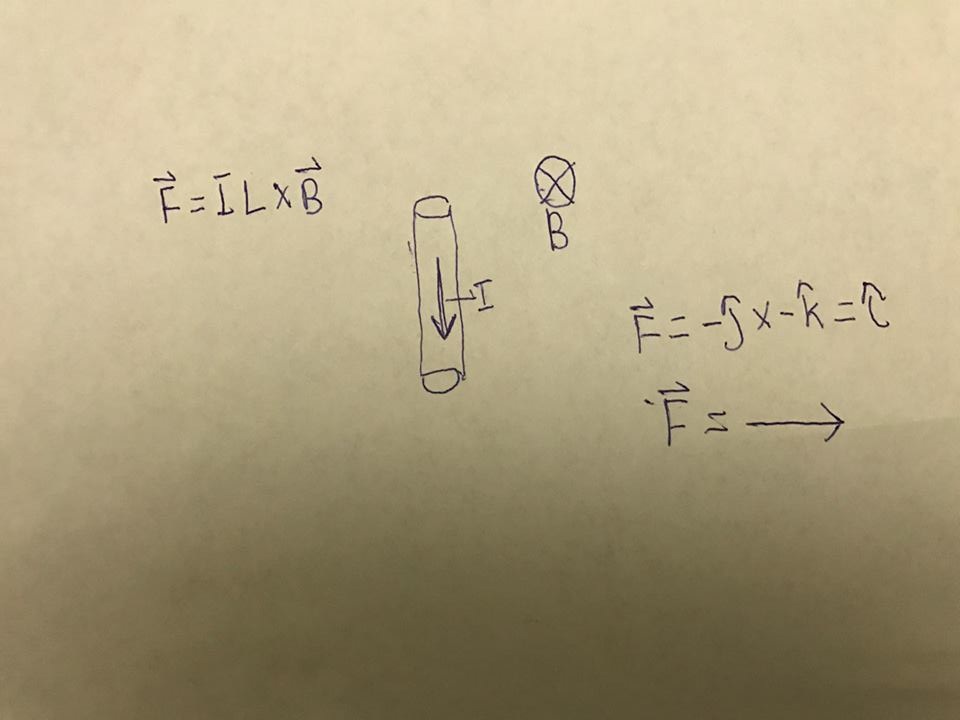Right-Hand Rule

Claimed by Alyssa Jackson Spring 2017 (09 April 2017)

The Main Idea

The Right-Hand Rule is an easy way to find the direction of a cross product interaction before doing the math. For any equation involving a cross product, the right hand rule is a valuable tool for finding the direction. There are two primary ways of using the right hand rule. The first method is to use your entire right hand. In the example below, the velocity is pointing north up and the magnetic field is pointing to the left. We place our hand with your thumb sticking up along the velocity since thats the first variable in F= qv X B. You curl your fingers towards the magnetic field. Your thumb is pointing upwards hence the direction of magnetic force is going out of the page. It is important to note that this only applies to positive charges. However, it is still very easy to find the direction of the right hand rule for negative charges. It is just the opposite direction for what you would do for positive charges.

A Mathematical Model

The Right-Hand Rule is mathamatically modeled by the cross product:

[math]\displaystyle{ \mathbf{u\times v}=(u_2v_3\mathbf{i}+u_3v_1\mathbf{j}+u_1v_2\mathbf{k}) -(u_3v_2\mathbf{i}+u_1v_3\mathbf{j}+u_2v_1\mathbf{k}) }[/math]

Alternate Method

If you are like me and for some particular reason it was hard to grasp the traditional method of carrying out a cross product, fear not! There is an alternate method that will lead you to the same answer in a more an intuitive manner.

This is a method I picked up a while back and has been proving quite useful since.1

It involves structuring the three components in a circle and assigning a clockwise direction around this circle.

Every time you cross one component with another component that can be reached clockwise on on the next move around the circle, you know that you will have a positive direction in the direction of the third direction.

This can be seen in the attached picture below.

In order to quickly solve a cross product using this alternate method, see the image below.

1 NOTE:I did not devise this method, but simply learned it.

Alternate Right Hand Rule

If you are like me, again, and constantly forget how to utilize the right hand rule correctly, there is a very simple trick associated with this method that can help.

Let us take a simple physics problem as an example. We know that :[math]\displaystyle{ \mathbf{F} = q\mathbf{v} \times \mathbf{B} }[/math]

Instead of using our right hand, we can just use the method pictured below to find the direction of the magnetic force given the direction of the moving particle and the magnetic field.

A Computational Model

The cross product is used to describe many magnetic interactions, for example, magnetic field created by a moving charge or a current and magnetic force on a particle by a magnetic field. Because of this, using the right hand rule, to determine the direction of a cross product, can be a useful to check behind the math for sign errors.

Follow the chart bellow to find which fingers correspond to which vectors.

[math]\displaystyle{ \mathbf{A\times B}=\mathbf{C} }[/math]

Vector	Right-hand	Right-hand (alternative)
A	First or index	Thumb
B	Second finger or palm	First or index
C	Thumb	Second finger or palm

Another method for determining the direction of the product orthogonal vector is to place the fingers of your right hand in the direction of the first vector(A). Curl your fingers in the direction of the second vector(B), effectively making the "thumbs up" sign in whichever direction the thumb happens to be pointing. The resulting vector(C) is in the direction in which your thumb is now pointing.

Examples

Magnetic Force on a Moving Particle

[math]\displaystyle{ \mathbf{F} = q\mathbf{v} \times \mathbf{B} }[/math]

The direction of the cross product may be found by application of the right hand rule as follows:

1. The index finger points in the direction of the momentum vector qv.
2. The middle finger points in the direction of the magnetic field vector B.
3. The thumb points in the direction of magnetic force F.

For example, for a positively charged particle moving to the right, in a region where the magnetic field points up, the resultant force points out of the page.

Magnetic Field made by a Current

[math]\displaystyle{ \mathbf{B} = \frac{\mu_0I}{4\pi}\int_{\mathrm{wire}}\frac{\mathrm{d}\boldsymbol{\ell} \times \mathbf{\hat r}}{r^2}, }[/math]

The direction of the cross product may be found by application of the right hand rule as follows:

1. The thumb points in the direction of current I.
2. The index finger points in the direction of the observation vector r.
3. The middle finger points in the direction of the magnetic field vector B.

Force on a Current from a Magnetic Field

[math]\displaystyle{ \mathbf{F} = \mathbf{I} \times \mathbf{B} }[/math]

The direction of the cross product may be found by application of the right hand rule as follows:

1. The index finger points in the direction of the current I.
2. The middle finger points in the direction of the magnetic field vector B.
3. The thumb points in the direction of magnetic force F.

For example, for a current moving into the page, in a region where the magnetic field points up, then the force is to the right of the current.

Another Force on a Current from a Magnetic Field

In the situation shown below, we have a current pointing downward or in the negative y direction and we have a magnetic field into the page or in the negative z direction. Instead of using the typical right hand rule, we can use easy cross product method below to find the direction of the force.

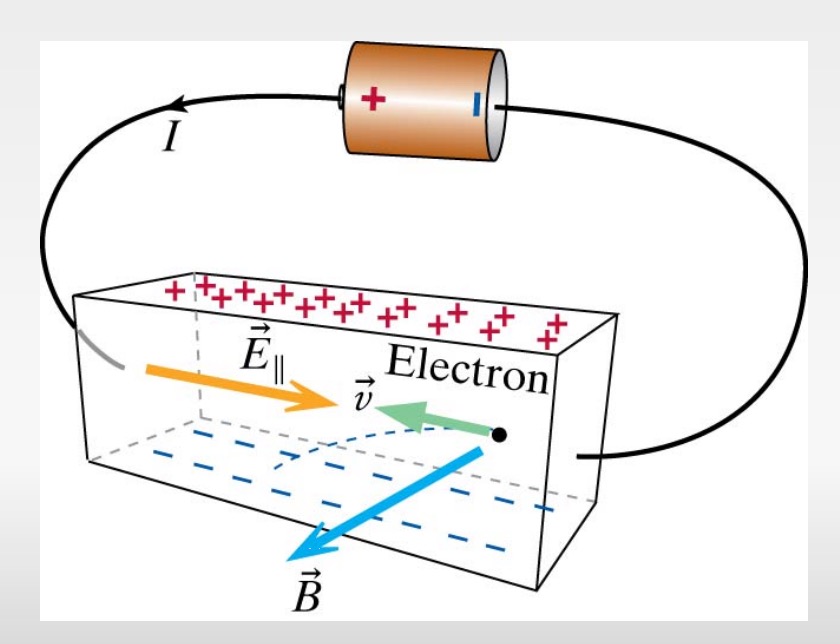
Hall Effect Example

In the above picture, you see that all the positive charges accumulated at the top and all the negative charges accumulated to the bottom. You know the direction the particles velocity and magnetic field. Can you find out the charge of the particle using the right hand rule?

In the picture, the particles are coming out of the negative terminal, so they are electrons. This can be verified by using the right hand rule. You curl your fingers from velocity vector to magnetic field vector to find the direction of magnetic force perpendicular. Your thumb is pointing up, but since these are negative charges, its opposite and you flip your hand and you find that the direction of the magnetic force is actually pointing down. Therefore it makes sense that the electrons would accumulate at the bottom since its magnetic force is pushing them towards there.

Connectedness

1. How is the topic connected to something you are interested in?

I am interested in its application to the Hall Effect on how charges accumulate in a conductor. I just fine it so interesting that such a simple tool allows us to find the direction of forcess, moving objects, and many other useful applications.

I have a genuine interest in its application to understanding and breaking down motion in three dimensions. Although, this is not strictly related to this class, it does involve physics very heavily.

2. How is it connected to your major?

As an industrial engineer, it has little application directly however, for those working in engineering physics and need to come up with a design. They could run into problems involving forces and velocity that require the right hand rule.

As a Mechanical Engineering major, this section is heavily related to a lot of what I do in many different classes. Knowing how to do cross products and the right hand rule has been crucial to understanding problems in Statics and Dynamics. In these classes, we deal with kinematics and kinetics in three dimensions and accordingly, the right hand rule and the alternate method of cross products are essential.

History

John Ambrose Fleming is credited with devising the right hand rule. He was a professor at the University College, London where he was liked by many of his students. He taught them how to easily determine the direction of a current. He made directional relationships easier between current, its magnetic field, and the electromotive force.

See Also

External Links

1. https://www.khanacademy.org/test-prep/mcat/physical-processes/magnetism-mcat/a/using-the-right-hand-rule
2. https://ocw.mit.edu/courses/physics/8-02t-electricity-and-magnetism-spring-2005/lecture-notes/prs_w06d1.pdf
3. http://physics.bu.edu/~duffy/semester2/d12_RHR_practice.html

References

1. https://en.wikipedia.org/wiki/Right-hand_rule
2. https://en.wikipedia.org/wiki/Magnetic_field
3. https://nationalmaglab.org/education/magnet-academy/history-of-electricity-magnetism/pioneers/john-ambrose-fleming

--Cjacobson7 (talk) 13:45, 10 November 2015 (EST)