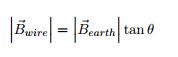Magnetic Dipole

Short Description of Topic Claimed by Jae Hyun Kim

The Main Idea

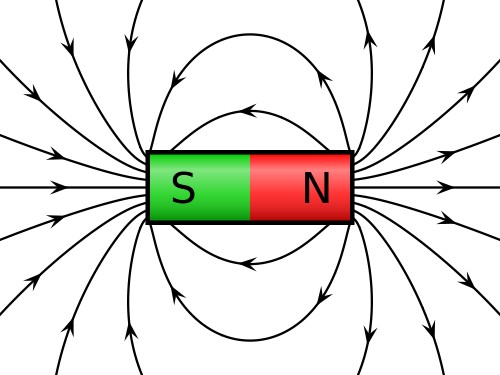
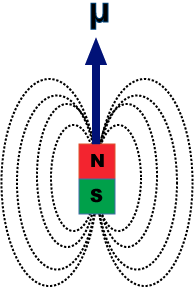
Dipole often occurs when there is a separation of charges, whether that be in a microscopic basis or macroscopic basis. When there are two separate poles of magnetism, a magnetic dipole forms, causing a unique pattern of magnetic field.

A Mathematical Model

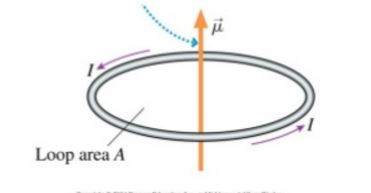
The main equation for a magnetic dipole is:

where I is the current, and A is the cross sectional area.

The 2nd part of the equation is specifically for loop field induced magnetic dipole and its area is naturally the area of a circle using the radius.

From this equation, we can deduce the magnetic dipole moments just knowing the conventional current flowing through the loop and the radius.

However, most of the time the current is not given. Furthermore, the equation is not applicable for the normal magnets that we see on life, for they do not have a electrical current flowing through. Thus, another way to get the dipole moment is by using the relationship between the magnetic dipole and the magnetic field induced by the dipole.

There are two equations based on the observation location.

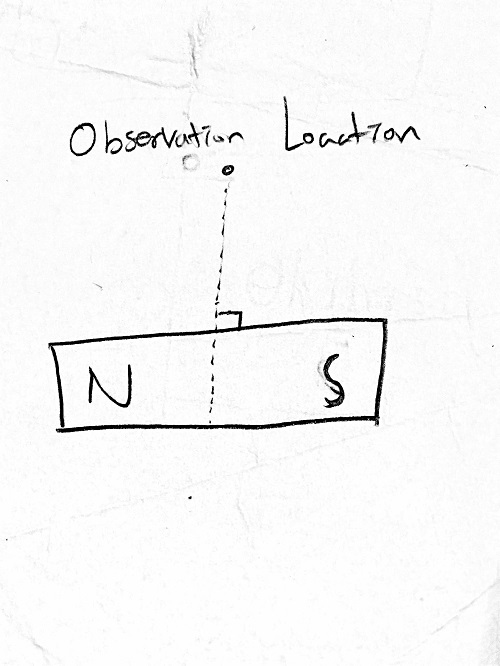
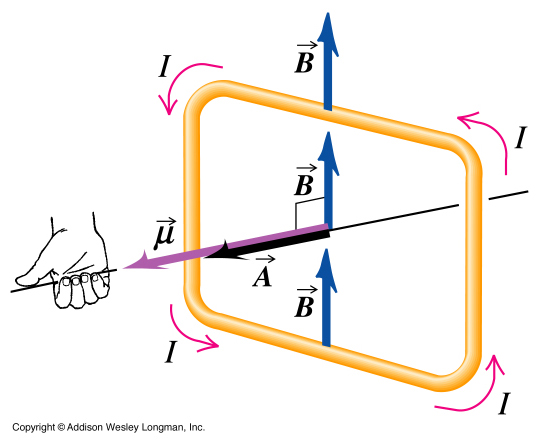
If the observation location is perpendicularly placed, meaning that the object is along the y axis of the dipole like the image below,

then the equation for the magnetic field induced by the dipole is:

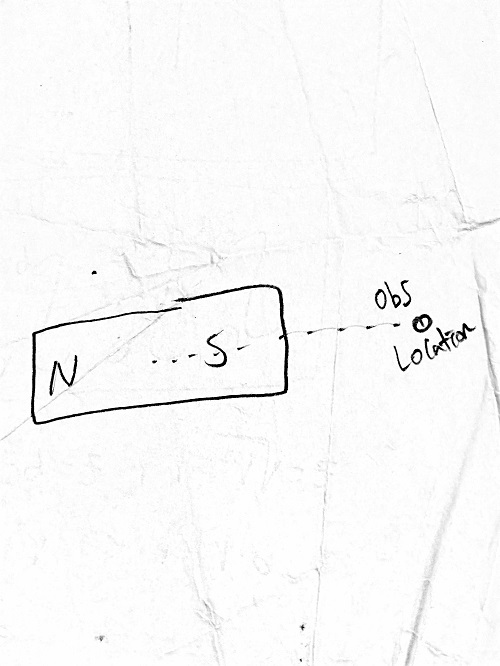
If the observation location is placed along the X axis like the image below

then the equation for the magnetic field induced by the dipole is:

The first part of the equation is the constant, 1E-7, and the other part of the equation requires the magnetic dipole and the distance between the observation location and the dipole denoted by r.

The most common form of problem using the magnetic dipole is as follows:

First, you would be given a compass and its deflection due to a magnet. Using this, you are able to figure out the magnetic field induced from the dipole using the equation:

where B earth is usually given to be 2E-5. Then, you will be able to calculate the magnetic field.

Using this magnetic field, you will be asked to calculate the magnetic dipole. The rest is simple; depending whether your compass was located perpendicularly or along the axis, you can choose which equation to use and plug in the values and solve for the magnetic dipole moment.

It is also important to note the direction of the dipole moment. The direction of the dipole moment points North in a magnet:

On the other hand, if you are looking at the dipole moment induced by a current-flowing loop, you have to use the right hand rule, make the hand curl in the direction of the current. The direction of your thumb will be the magnetic dipole moment induced from the current.

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

In a circular loop with current of 3 Ampere and diameter of 16 cm, what is the magnetic dipole moment induced from the current?

Solution

We can just simply use the first equation given in the beginning:

where R is 0.08 meters and I is 3 Amperes. Calculating for the magnetic dipole moment gives:

[math]\displaystyle{ 3 \times 0.08^2 \times \pi = 0.0192 }[/math]

Middling

When the compass was placed 20 cm away from a bar magnet parallel to the X axis and showed deflection of 20 degrees, what is the magnetic dipole of the magnet? You can assume that B earth is 2E-5

Solution

First, we need to figure out the magnetic dipole induced from the magnet. Thus, we need to use the formula:

where B earth is 2E-5, and the degree is 20 degrees. Thus,

[math]\displaystyle{ 2E-5 \times tan(20) = 7.3E-6 }[/math]

With the given magnetic field, we can plug in the value into the formula given (note that because it is along the X axis, we use this formula)

<math> 7.3E-6 = 2 \times

Connectedness

1. How is this topic connected to something that you are interested in?
2. How is it connected to your major?
3. Is there an interesting industrial application?

History

Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.

See also

Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

Further reading

Books, Articles or other print media on this topic

External links

Internet resources on this topic

References

This section contains the the references you used while writing this page