Vectors

Written by Elizabeth Robelo

Improved by: Aparajita Satapathy

In physics, a vector is an object with a magnitude and a direction.

The Main Idea

A vector is an object with a magnitude and a direction. The magnitude of a vector is a scalar which represents the length of the vector. A vector is represented by an arrow. The orientation of the vector represents its direction. When a vector is drawn, the starting point is the tail and the ending point is called the head of the vector. Refer to the image below for a visual representation:

Visual Representation

We can also add and subtract vectors. To add two vectors you align them head to tail and make sure that the tails of both vectors coincide with each other. The new added vector is the connecting arrow starting from the tail of one to the head of the other vector.

Adding vector A to B

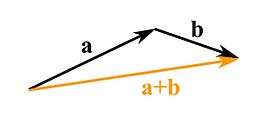
To subtract two vectors reverse the direction of the vector you want to subtract and continue to add them like shown before.

Subtracting vector B from A

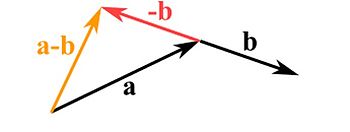
A vector can also be multiplied by a scalar. To multiply a vector by a scalar we can strech, compress or reverse the direction of a vector. If the scalar is between 0 and 1, the vector will be compresseed. If the scalar is greater than 1, the vector will get streched. If the scalar is a negative number, then the vector reverses its direction.

Scalar Multiplication

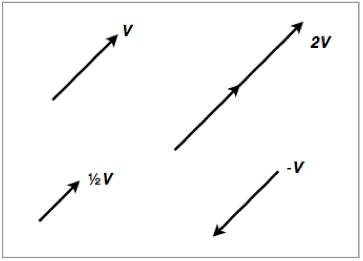
A Mathematical Model

Vectors are given by x, y, and z coordinates. They are written in the form <x, y, z> or xi + yj - zk. Magnitude: [math]\displaystyle{ |A| = \sqrt{x^2 + y^2 + z^2} }[/math]

Dot Product: [math]\displaystyle{ \mathbf{A}\cdot\mathbf{B}=\sum_{i=1}^n A_iB_i=A_1B_1+A_2B_2+\cdots+A_nB_n }[/math]

[math]\displaystyle{ \lt x1, x2, x3\gt \cdot \lt y1, y2, y3\gt &= (x1)(y1) + (x2)(y2) + (x3)(y3) \\ \end{align} }[/math]

Addition of two vectors: <a1, a2, a3> + <b1, b2, b3> = <a1 + b1, a2 + b2, a3 + b3>

Unit Vector: :[math]\displaystyle{ \mathbf{\hat{u}} = \frac{\mathbf{u}}{\|\mathbf{u}\|} }[/math]

A Computational Model

Here you have vpython code creating a vector from one object to another. vectors

Examples

Simple

Which of the following statements is correct?

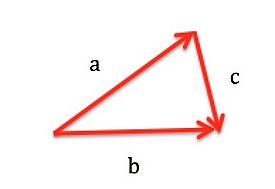
1. [math]\displaystyle{ \overrightarrow{c} = \overrightarrow{b} + \overrightarrow{a} }[/math]

2. [math]\displaystyle{ \overrightarrow{a} = \overrightarrow{b} - \overrightarrow{c} }[/math]

3. [math]\displaystyle{ \overrightarrow{a} = \overrightarrow{b} + \overrightarrow{c} }[/math]

4. [math]\displaystyle{ \overrightarrow{b} = \overrightarrow{a} + \overrightarrow{c} }[/math]

The answer is 2.

Middling

What is the magnitude of the vector C = A - B if A = <6, 21, 17> and B = <12, 7, 15>?

A - B = [math]\displaystyle{ \lt 6-12, 21-7, 17-15\gt = \lt -6, 14, 2\gt = C }[/math]

[math]\displaystyle{ \sqrt{(-6)^2 + 14^2 + 2^2} = 15.36 }[/math]

Difficult

What is the unit vector in the direction of the vector <12, -15, 9>? First you have to find the magnitude of the vector given: [math]\displaystyle{ \sqrt{12^2 + (-15)^2 + 9^2} = 21.21 }[/math]

Finally divide the vector by its magnitude to get the unit vector:

[math]\displaystyle{ \tfrac{\lt 12,-15,9\gt }{180} }[/math]

= <.565, -.707, .424>

Applications

You will use vectors for everything in physics ranging from velocity to gravitational field.

History

Giusto Bellavitis abstracted the basic idea of a vector in 1835 when he established the concept of equipollence. He called any pair of line segments of the same length and orientation equipollent. He found a relationship and created the first set of vectors.

The name vector was given to us by William Rowan Hamilton as part of his system of quaternions. The vectors he used were three dimensional.

Several other mathematicians developed similar vector systems to those of Bellavitis and Hamilton in the 19th century. The system used by Herman Grassman is the one that is most similar to the one used today. He thought of ideas similar to the cross product and vector differentiation.

See also

External links

[1]

References

https://www.mathsisfun.com/algebra/vectors.html

http://ocw.mit.edu/courses/mathematics/18-02sc-multivariable-calculus-fall-2010/1.-vectors-and-matrices/part-a-vectors-determinants-and-planes/session-1-vectors/MIT18_02SC_notes_0.pdf

https://en.wikipedia.org/wiki/Euclidean_vector#Addition_and_subtraction