Coefficient of Restitution

Claimed by Maria Moreno

The coefficient of restitution measures the elasticity of a collision.

The Main Idea

The coefficient of restitution is a ratio that describes the degree of elasticity of a collision. It is used to solve problems dealing with collisions that are not perfectly elastic or inelastic. The equation that describes the coefficient of restitution involved dividing the difference in the final velocities by the difference in the initial velocity.

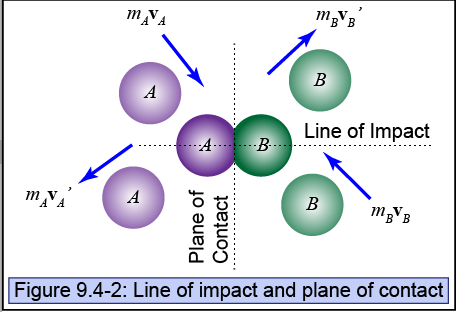
Consider objects A and B with initial velocities v_Ai and v_Bi and final velocities v_Af and v_Bf. The coefficient of restitution, e is determined with the following formula:

[math]\displaystyle{ e = \frac{v_{Bf}-v_{Af}}{v_{Ai}-v_{Bi}} }[/math]

A Mathematical Model

Consider a perfectly elastic collision between objects A and B where v_Ai and v_Bi refer to the initial velocities of A and B and v_Af and v_Bf refer to the final velocities of A and B.

Start with the conservation of momentum principle which states that
[math]\displaystyle{ \vec{p_i} = \vec{p_f} }[/math]
and
[math]\displaystyle{ m_A\vec{v_{Ai}}+m_A\vec{v_{Bi}}=m_A\vec{v_{Af}}+m_A\vec{v_{Bf}} }[/math] (1)

Remember that for a perfectly elastic collision kinetic energy is also conserved meaning:
[math]\displaystyle{ \vec{KE_i} = \vec{KE_f} }[/math]
and
[math]\displaystyle{ \frac{1}{2}m_A \vec{v^2_{Ai}}+\frac{1}{2}m_A \vec{v^2_{Bi}}=\frac{1}{2}m_A \vec{v^2_{Af}}+\frac{1}{2}m_A \vec{v^2_{Bf}} }[/math] (2)

Dividing (2) by (1) yields:

[math]\displaystyle{ \vec{v_{Ai}}+\vec{v_{Bi}}=\vec{v_{Af}}+\vec{v_{Bf}} }[/math]
[math]\displaystyle{ 1=\frac{\vec{v_{Ai}}+\vec{v_{Bi}}}{\vec{v_{Af}}+\vec{v_{Bf}}} }[/math]

[math]\displaystyle{ e=\frac{\vec{v_{Ai}}+\vec{v_{Bi}}}{\vec{v_{Af}}+\vec{v_{Bf}}} }[/math]

For perfectly elastic collision e=1.

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Difficult

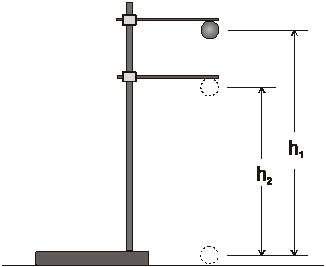
Bouncing Ball Example:

Connectedness

How is this topic connected to something that you are interested in?
How is it connected to your major (Mechanical Engineering)?
The coefficient of restitution is a key concept in the study of Dynamics which is the foundation of many aspects of mechanical engineering.

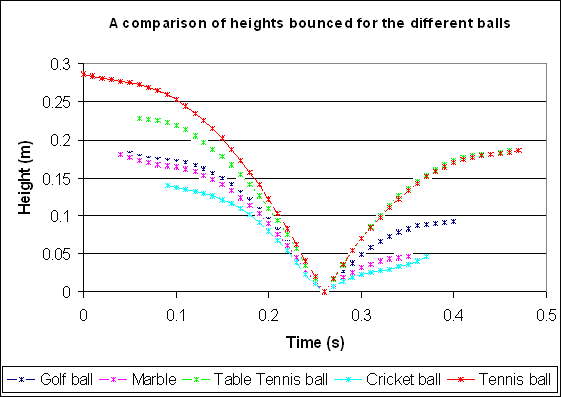
Is there an interesting industrial application? In sports the coefficient of restitution is an important concept especially in sports like golf or tennis where collisions are a frequent and essential part of the game. In these sports sometimes limitations are put on how high the coefficient of restitution can be for certain clubs or bats. The maximum coefficient of restitution allowed in golf for clubs is .82. There have been studies done on the coefficients for different sports balls.

See also

Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

Further reading

Books, Articles or other print media on this topic

References

This section contains the the references you used while writing this page