Boiling Point: Difference between revisions

From Physics Book
Jump to navigation Jump to search
No edit summary
No edit summary
Line 1: Line 1:
'''Claimed and edited by Chris Li (Fall 2025)'''
'''Claimed by Chris Li (Fall 2025)'''


==The Main Idea==
==The Main Idea==


The boiling point of a liquid is the temperature at which its vapor pressure becomes equal to the external pressure around it, allowing the liquid to transition into vapor. Because vapor pressure depends on temperature, the boiling point changes when pressure changes. At high external pressure, a liquid boils at a higher temperature; at low external pressure (such as at high altitudes or in a partial vacuum), the boiling point is lower.  
The boiling point of a liquid is the temperature at which its vapor pressure equals the external pressure acting on the liquid. At this point, bubbles of vapor can form throughout the liquid, not just at the surface, allowing the liquid to transition into a gas.


Boiling point also varies from substance to substance, since different liquids have different intermolecular forces and vapor pressure curves. These principles are important for chemistry, cooking, engineering, distillation, and everyday processes involving heat transfer.
Because vapor pressure changes rapidly with temperature, the boiling point is not a fixed property—rather, it depends on:
 
* **External pressure** (higher pressure → higher boiling point; lower pressure → lower boiling point)
* **Chemical composition** (different liquids boil at different temperatures)
* **Solutes dissolved in the liquid**, which raise the boiling point (a colligative property)
 
Boiling point is important in thermodynamics, cooking, meteorology, chemical engineering, distillation, and phase equilibrium.
 
[[File:Boiling-water.jpg|center|350px|thumb|Boiling occurs when vapor pressure equals external pressure.]]
 
---


===A Mathematical Model===
===A Mathematical Model===
Two major equations help model boiling point behavior: the Clausius–Clapeyron equation and the boiling point elevation equation.
 
Boiling phenomena can be described mathematically using two major relationships:
 
* **Clausius–Clapeyron Equation** → relates vapor pressure and temperature 
* **Boiling Point Elevation Equation** → describes how dissolved solutes raise the boiling point


----
----
Line 14: Line 28:
'''Clausius–Clapeyron Equation'''
'''Clausius–Clapeyron Equation'''


This equation is used when the vapor pressure at one temperature and the heat of vaporization are known, and the goal is to determine the boiling point at a different pressure.
Used to calculate the boiling temperature at a new pressure when ΔH<sub>vap</sub> and a reference boiling point are known.
 
\[
\ln\left(\frac{P}{P_0}\right)
= -\frac{\Delta H_{vap}}{R} \left( \frac{1}{T_B} - \frac{1}{T_0} \right)
\]


[[File:ClausiusClapeyron.png]]
[[File:ClausiusClapeyron.png|center|Graph of vapor pressure vs temperature illustrating boiling point.]]


''Constants in the equation:''
''Variable definitions:''


* '''T<sub>B</sub>''' – boiling temperature at pressure P   
* '''T<sub>B</sub>''' – boiling temperature at pressure P   
* '''T<sub>0</sub>''' – reference temperature corresponding to pressure P<sub>0</sub>
* '''T<sub>0</sub>''' – known temperature at pressure P<sub>0</sub>   
* '''R''' – ideal gas constant (8.314 J·mol<sup>−1</sup>·K<sup>−1</sup>)  
* '''P''' – new vapor pressure   
* '''P''' – vapor pressure at desired boiling conditions  
* '''P<sub>0</sub>''' – reference vapor pressure   
* '''P<sub>0</sub>''' – vapor pressure at reference conditions  
* '''ΔH<sub>vap</sub>''' – heat of vaporization   
* '''ΔH<sub>vap</sub>''' – heat of vaporization   
* '''R''' – ideal gas constant (8.314 J·mol<sup>−1</sup>·K<sup>−1</sup>)


----
----
Line 31: Line 50:
'''Boiling Point Elevation Equation'''
'''Boiling Point Elevation Equation'''


This describes how adding a solute to a solvent increases its boiling point:
Dissolving solute particles raises the boiling point of a solvent:
 
\[
\Delta T_b = K_b \, b_B
\]
 
Where:


'''ΔT<sub>b</sub> = K<sub>b</sub> · b<sub>B</sub>'''
* '''ΔT<sub>b</sub>''' = T<sub>b,solution</sub> − T<sub>b,solvent</sub> 
* '''K<sub>b</sub>''' = ebullioscopic constant 
* '''b<sub>B</sub>''' = effective molality: b<sub>solute</sub> · i 
* '''i''' = van’t Hoff factor 


''Where:''
[[File:BoilingPointElevation.png|center|350px|thumb|Boiling point elevation vs solute concentration.]]


* '''ΔT<sub>b</sub>''' – boiling point elevation (T<sub>b,solution</sub> − T<sub>b,solvent</sub>) 
This equation is central in colligative property analysis.
* '''K<sub>b</sub>''' – [[Ebullioscopic constant]] 
* '''b<sub>B</sub>''' – molality of solute particles, b<sub>B</sub> = b<sub>solute</sub> · i 
* '''i''' – van't Hoff factor (number of dissolved particles produced per solute molecule)


These equations model how temperature, pressure, and solute concentration affect boiling point.
---


===A Computational Model===
===A Computational Model===


A computational model for boiling point elevation begins by defining relevant constants:
We can simulate boiling point elevation or vapor-pressure curves numerically. The following VPython/GlowScript code models the Clausius–Clapeyron equation to generate a vapor pressure vs temperature plot:
 
<syntaxhighlight lang="python">
import numpy as np
import matplotlib.pyplot as plt
 
R = 8.314
Hv = 40000    # J/mol
T0 = 373.15  # K
P0 = 101325  # Pa
 
T = np.linspace(320, 400, 200)
P = P0 * np.exp(-Hv/R * (1/T - 1/T0))
 
plt.plot(T, P)
plt.xlabel("Temperature (K)")
plt.ylabel("Vapor Pressure (Pa)")
plt.title("Vapor Pressure Curve via Clausius-Clapeyron")
plt.show()
</syntaxhighlight>
 
This simulation demonstrates how small temperature changes dramatically affect vapor pressure, explaining why boiling point shifts with altitude and pressure.
 
A second computational model simulates boiling point elevation:


* K<sub>b</sub> = ebullioscopic constant 
<syntaxhighlight lang="python">
* b<sub>solute</sub> = molality of the solute 
Kb = 0.512          # water
* i = van’t Hoff factor 
m = np.linspace(0, 5, 200)  # molality range
* b<sub>B</sub> = b<sub>solute</sub> · i
i = 2              # NaCl (approx)
Tb = 100 + Kb * m * i


Then compute:
plt.plot(m, Tb)
plt.xlabel("Molality (m)")
plt.ylabel("Boiling Point (°C)")
plt.title("Boiling Point Elevation for NaCl in Water")
plt.show()
</syntaxhighlight>


'''ΔT<sub>b</sub> = K<sub>b</sub> · b<sub>B</sub>'''
These visual models help make the equations intuitive.


A program can simulate increasing solute concentration and produce a temperature–concentration graph showing how boiling point rises.
---


==Examples==
==Examples==


Below are structured examples following the Physics Book template.
Below are expanded, step-by-step examples.


===Simple===
===Simple===


A 1.0 m NaCl solution (i = 2) is prepared in water with K<sub>b</sub> = 0.512 K·kg/mol.
A 1.0 m NaCl solution (i = 2) is prepared in water with K<sub>b</sub> = 0.512 °C·kg/mol.
 
\[
\Delta T_b = (0.512)(1.0)(2) = 1.024^\circ C
\]


ΔT<sub>b</sub> = (0.512)(1.0)(2) = 1.024°C 
\[
T<sub>b</sub> = 100°C + 1.024°C = 101.024°C
T_b = 100^\circ C + 1.024^\circ C = 101.024^\circ C
\]


===Middling===
===Middling===


A substance has vapor pressure P<sub>0</sub> = 0.80 atm at T<sub>0</sub> = 360 K.
A liquid boils at 360 K under 0.80 atm. What is its boiling temperature under 1.00 atm? 
Find T<sub>B</sub> at pressure P = 1.00 atm using Clausius–Clapeyron and ΔH<sub>vap</sub> = 32,000 J/mol.
Given: ΔH<sub>vap</sub> = 32 kJ/mol.


<math>
\[
\ln\left(\frac{1.00}{0.80}\right)
\ln\left(\frac{1.00}{0.80}\right)  
= -\frac{32000}{8.314}\left(\frac{1}{T_B} - \frac{1}{360}\right)
= -\frac{32000}{8.314}\left(\frac{1}{T_B} - \frac{1}{360}\right)
</math>
\]


Solving gives T<sub>B</sub> ≈ 372 K.
Solving gives: 
\[
T_B \approx 372\ \text{K}
\]


===Difficult===
===Difficult===


A liquid has P<sub>1</sub> = 0.50 atm at T<sub>1</sub> = 300 K and P<sub>2</sub> = 1.20 atm at T<sub>2</sub>.   
A liquid has vapor pressure 0.50 atm at 300 K and 1.20 atm at an unknown temperature T<sub>2</sub>.   
Assume ΔH<sub>vap</sub> is constant.
 
Use the two-point Clausius–Clapeyron form:
Use the two-point Clausius–Clapeyron form:


<math>
\[
\ln\left(\frac{1.20}{0.50}\right)
\ln\left(\frac{1.20}{0.50}\right)
= -\frac{\Delta H_{vap}}{R}\left(\frac{1}{T_2} - \frac{1}{300}\right)
= -\frac{\Delta H_{vap}}{R}\left(\frac{1}{T_2} - \frac{1}{300}\right)
</math>
\]
 
Solving:


Solving yields T<sub>2</sub> ≈ 345 K.
\[
T_2 \approx 345\ \text{K}
\]


More practice problems can be found here:   
More problems:   
[http://www.chemteam.info/Solutions/BP-elevation-probs1-to-10.html Boiling Point Elevation]
[http://www.chemteam.info/Solutions/BP-elevation-probs1-to-10.html Boiling Point Elevation]
---


==Connectedness==
==Connectedness==
Boiling point is crucial in real-world applications:


* **Cooking:** Adding salt slightly raises boiling point (though only by a small amount).   
Boiling point matters in many real-world contexts:
* **Chemical engineering:** Boiling and vaporization are central to distillation, separation, and refining.   
 
* **Food and sugar processing:** Syrup concentration changes boiling temperature, which indicates sugar content.   
* **Cooking:** Salt slightly raises water’s boiling temperature; pressure cookers increase pressure to cook food faster.   
* **Environmental science:** Atmospheric pressure variations affect evaporation and boiling.
* **Chemical engineering:** Distillation relies entirely on different boiling points. 
* **Meteorology:** Atmospheric pressure affects evaporation and cloud formation.   
* **Food production:** Sugar concentration is monitored via boiling temperature in candy-making.   
* **Medicine:** Autoclaves use high-pressure steam to sterilize tools. 
 
Boiling point connects physics, chemistry, engineering, and environmental science.


This topic connects strongly to chemistry, thermodynamics, and material science.
---


==History==
==History==


In 1741, Anders Celsius proposed a temperature scale using the boiling and melting points of water.   
* **Ancient origins:** Philo and Hero of Alexandria described early thermometric principles and steam devices. 
Earlier Greek scientists such as Philo and Hero of Alexandria described primitive thermometric principles and explored steam power concepts.   
* **1741:** Anders Celsius defined his temperature scale using the boiling and melting points of water (later reversed to the modern form).   
Celsius originally labeled the boiling point as 0° and freezing point as 100°, which was later reversed to form the modern Celsius scale.
* **19th century:** Clapeyron and Clausius formalized the vapor‐pressure–temperature relationship, laying the foundation for phase diagrams and thermodynamics.   
 
The study of boiling was central to the development of thermometers, steam engines, and modern heat science.
 
---


==See also==
==See also==
* [[Melting Point]]
 
* [[Vapor Pressure]]
* [[Melting Point]]
* [[Clausius–Clapeyron Equation]]
* [[Vapor Pressure]]
* [[Phase Diagram]]
* [[Clausius–Clapeyron Equation]]
* [[Phase Diagram]]
* [[Colligative Properties]] 


===Further reading===
===Further reading===


* [https://www.chem.purdue.edu/gchelp/liquids/boil.html Boiling – Purdue Chemistry]   
* [https://www.chem.purdue.edu/gchelp/liquids/boil.html Purdue – Boiling]   
* [http://www.britannica.com/science/boiling-point Boiling Point – Britannica]
* [http://www.britannica.com/science/boiling-point Britannica – Boiling Point]


===External links===
===External links===
Line 133: Line 209:


* [http://www.ehow.com/info_8344665_uses-boiling-point-elevation.html Uses of Boiling Point Elevation]   
* [http://www.ehow.com/info_8344665_uses-boiling-point-elevation.html Uses of Boiling Point Elevation]   
* [http://www.chemteam.info/Solutions/BP-elevation.html Boiling Point Elevation Problems]   
* [http://www.chemteam.info/Solutions/BP-elevation.html Boiling Point Elevation]   
* [https://www.chem.tamu.edu/class/majors/tutorialnotefiles/intext.htm Chemistry Basics – TAMU]   
* [https://www.chem.tamu.edu/class/majors/tutorialnotefiles/intext.htm Chemistry Basics]   
* [http://chemed.chem.purdue.edu/genchem/topicreview/bp/ch14/melting.php Melting/Freezing/Boiling Points – Purdue]   
* [http://chemed.chem.purdue.edu/genchem/topicreview/bp/ch14/melting.php Melting / Freezing / Boiling]   
* [http://didyouknow.org/celsius/ Boiling Point of Water]   
* [http://didyouknow.org/celsius/ Boiling Point of Water]   


[[Category:Properties of Matter]]
[[Category:Properties of Matter]]

Revision as of 21:57, 1 December 2025

Claimed by Chris Li (Fall 2025)

The Main Idea

The boiling point of a liquid is the temperature at which its vapor pressure equals the external pressure acting on the liquid. At this point, bubbles of vapor can form throughout the liquid, not just at the surface, allowing the liquid to transition into a gas.

Because vapor pressure changes rapidly with temperature, the boiling point is not a fixed property—rather, it depends on:

  • **External pressure** (higher pressure → higher boiling point; lower pressure → lower boiling point)
  • **Chemical composition** (different liquids boil at different temperatures)
  • **Solutes dissolved in the liquid**, which raise the boiling point (a colligative property)

Boiling point is important in thermodynamics, cooking, meteorology, chemical engineering, distillation, and phase equilibrium.

Boiling occurs when vapor pressure equals external pressure.

---

A Mathematical Model

Boiling phenomena can be described mathematically using two major relationships:

  • **Clausius–Clapeyron Equation** → relates vapor pressure and temperature
  • **Boiling Point Elevation Equation** → describes how dissolved solutes raise the boiling point

Clausius–Clapeyron Equation

Used to calculate the boiling temperature at a new pressure when ΔHvap and a reference boiling point are known.

\[ \ln\left(\frac{P}{P_0}\right) = -\frac{\Delta H_{vap}}{R} \left( \frac{1}{T_B} - \frac{1}{T_0} \right) \]

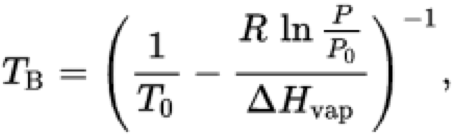
Graph of vapor pressure vs temperature illustrating boiling point.
Graph of vapor pressure vs temperature illustrating boiling point.

Variable definitions:

  • TB – boiling temperature at pressure P
  • T0 – known temperature at pressure P0
  • P – new vapor pressure
  • P0 – reference vapor pressure
  • ΔHvap – heat of vaporization
  • R – ideal gas constant (8.314 J·mol−1·K−1)

Boiling Point Elevation Equation

Dissolving solute particles raises the boiling point of a solvent:

\[ \Delta T_b = K_b \, b_B \]

Where:

  • ΔTb = Tb,solution − Tb,solvent
  • Kb = ebullioscopic constant
  • bB = effective molality: bsolute · i
  • i = van’t Hoff factor
Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127
Boiling point elevation vs solute concentration.

This equation is central in colligative property analysis.

---

A Computational Model

We can simulate boiling point elevation or vapor-pressure curves numerically. The following VPython/GlowScript code models the Clausius–Clapeyron equation to generate a vapor pressure vs temperature plot:

<syntaxhighlight lang="python"> import numpy as np import matplotlib.pyplot as plt

R = 8.314 Hv = 40000 # J/mol T0 = 373.15 # K P0 = 101325 # Pa

T = np.linspace(320, 400, 200) P = P0 * np.exp(-Hv/R * (1/T - 1/T0))

plt.plot(T, P) plt.xlabel("Temperature (K)") plt.ylabel("Vapor Pressure (Pa)") plt.title("Vapor Pressure Curve via Clausius-Clapeyron") plt.show() </syntaxhighlight>

This simulation demonstrates how small temperature changes dramatically affect vapor pressure, explaining why boiling point shifts with altitude and pressure.

A second computational model simulates boiling point elevation:

<syntaxhighlight lang="python"> Kb = 0.512 # water m = np.linspace(0, 5, 200) # molality range i = 2 # NaCl (approx) Tb = 100 + Kb * m * i

plt.plot(m, Tb) plt.xlabel("Molality (m)") plt.ylabel("Boiling Point (°C)") plt.title("Boiling Point Elevation for NaCl in Water") plt.show() </syntaxhighlight>

These visual models help make the equations intuitive.

---

Examples

Below are expanded, step-by-step examples.

Simple

A 1.0 m NaCl solution (i = 2) is prepared in water with Kb = 0.512 °C·kg/mol.

\[ \Delta T_b = (0.512)(1.0)(2) = 1.024^\circ C \]

\[ T_b = 100^\circ C + 1.024^\circ C = 101.024^\circ C \]

Middling

A liquid boils at 360 K under 0.80 atm. What is its boiling temperature under 1.00 atm? Given: ΔHvap = 32 kJ/mol.

\[ \ln\left(\frac{1.00}{0.80}\right) = -\frac{32000}{8.314}\left(\frac{1}{T_B} - \frac{1}{360}\right) \]

Solving gives: \[ T_B \approx 372\ \text{K} \]

Difficult

A liquid has vapor pressure 0.50 atm at 300 K and 1.20 atm at an unknown temperature T2. Use the two-point Clausius–Clapeyron form:

\[ \ln\left(\frac{1.20}{0.50}\right) = -\frac{\Delta H_{vap}}{R}\left(\frac{1}{T_2} - \frac{1}{300}\right) \]

Solving:

\[ T_2 \approx 345\ \text{K} \]

More problems: Boiling Point Elevation

---

Connectedness

Boiling point matters in many real-world contexts:

  • **Cooking:** Salt slightly raises water’s boiling temperature; pressure cookers increase pressure to cook food faster.
  • **Chemical engineering:** Distillation relies entirely on different boiling points.
  • **Meteorology:** Atmospheric pressure affects evaporation and cloud formation.
  • **Food production:** Sugar concentration is monitored via boiling temperature in candy-making.
  • **Medicine:** Autoclaves use high-pressure steam to sterilize tools.

Boiling point connects physics, chemistry, engineering, and environmental science.

---

History

  • **Ancient origins:** Philo and Hero of Alexandria described early thermometric principles and steam devices.
  • **1741:** Anders Celsius defined his temperature scale using the boiling and melting points of water (later reversed to the modern form).
  • **19th century:** Clapeyron and Clausius formalized the vapor‐pressure–temperature relationship, laying the foundation for phase diagrams and thermodynamics.

The study of boiling was central to the development of thermometers, steam engines, and modern heat science.

---

See also

Further reading

External links

References

Retrieved from "http://www.physicsbook.gatech.edu/index.php?title=Boiling_Point&oldid=47636"