Potential Difference in an Insulator

Claimed by Ava Sadasivan Fall 2025

Potential difference is defined as a scalar quantity that measures the difference of energy per unit charge. This page will not go over how to calculate electric potential in a conductor (because other pages cover this topic), but rather, how to find the electric potential in an insulator given the potential difference in a vacuum.

Main Idea

Potential difference between two points is dependent on two variables: the electric field and the distance between the two points. To be specific, potential difference is the path-integral of the electric field. This value is found by taking the dot product of the electric field and the distance between both points.

Net Electric Field Inside an Insulator

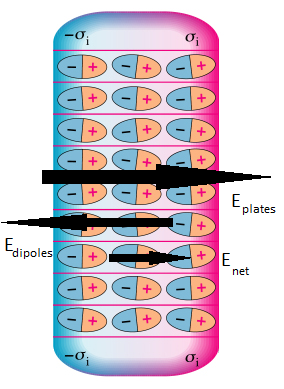
In a conductor, charges are free to move around and rearrange. Because of this, we know that between any two points inside of a conductor in equilibrium, the potential difference is zero. However, inside an insulator, this is not the case. When an insulator is placed in an external electric field (like between capacitor plates), the molecules inside it become polarized. This means that they slightly shift and create induced dipoles. These dipoles produce their own electric field, which opposes the external one.

The net electric field then equals the applied electric field minus the electric field from the dipoles. This net field still points in the same direction as the applied field, but it is weaker because the dipoles partially cancel it. Because the electric field is not zero, the potential difference between two points in the insulator is also not zero.

Round Trip Potential Difference

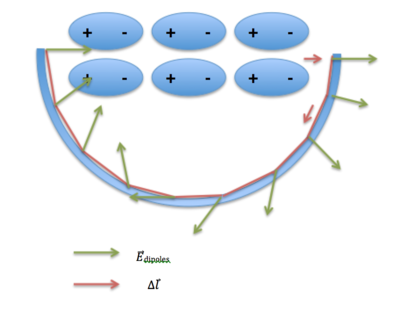
Although the pattern of the electric field created by the dipoles inside the insulator is complex, the pattern of the electric field outside the insulator is much easier to tell. When you go around any closed loop, the potential change must be zero.

Why? As you walk around the loop, the direction of the electric field and the direction of your path contribute both positive and negative values. This, once summed around the circumference of the loop, fully cancels out.

A Mathematical Model

Dielectric Constant

Placing an insulator between the plates of a capacitor would decrease the electric field inside the insulator and decrease potential difference across the insulator. When solving for the potential difference in an insulator, we define the constant K as the dielectric constant. This quantity represents the amount by which the net electric field is "weakened" due to the induced dipoles. The dielectric constant is related to the atomic polarizability. It is a value typically known through previous scientific experimentation (specifically, measuring the effect of an insulator on the potential difference between two charged objects).

Electric Field Inside an Insulator

[math]\displaystyle{ \vec {E}_{insulator} = \frac{\vec{E}_{applied}}{K} }[/math]

The dielectric constant K is always greater than one if an insulator is present because the induced dipoles in the polarized insulator always weaken the net electric field. When an insulating substance is easy to polarize, K will be large because the induced dipoles will create a weaker net electric field. If there is no insulating material between the charged objects (the space is a vacuum), K equals one.

The cases we discussed above only concern the spaces occupied by the insulator. If the insulator only fits part of the capacitor, the spaces it filled will be reduced by the factor K but the rest of the place will hardly be influenced.

Relating Electric Field to Potential Difference

Because the relationship between the electric field and potential difference is proportional, potential difference will also decrease by a value K. That is, placing an insulator in between two charged objects- like the plates of a capacitor- also decreases potential difference across the insulator. It is important to note that if the insulator does not fill the gap between objects, the electric field and potential difference inside the insulator are still reduced by a factor K. However, the areas that are not filled by the insulator are not affected since the electric field inside the insulator is negligibly small.

Potential Difference Inside an Insulator

[math]\displaystyle{ \Delta{V}_{insulator} = \frac{\Delta{V}_{vacuum}}{K} }[/math]

A Computational Model

Here is a Glowscript demo of a parallel-plate capacitor with and without an insulator. This demonstrates how the electric field and potential difference change when you change the dielectric constant K (reminder: K is the amount an insulator reduces an electric field inside it compared to a vacuum).

Link to model: https://www.glowscript.org/#/user/avarose.sadasivan/folder/MyPrograms/program/PotentialDifferenceInsulator

How To Use This Model:

The red and blue blocks are the capacitor plates. The blue plate is the negative plate and red plate is the positive plate, separated by a distance d. The space between them is where the electric field exists. These plates create a uniform electric field when nothing is between them (a vacuum).

The orange arrows are the electric field lines. Each arrow shows the direction of the electric field (from the positive plate to the negative plate). The length of each arrow represents the magnitude of the electric field (longer = stronger magnetic field).

If you insert an insulator (increase K), the field becomes weaker, so the arrows shrink.

Beyond the visual, this computational model also computes and displays some key values.

• K — the dielectric constant
• E_vac — the electric field when the space is a vacuum
• ΔV_vac — the potential difference in a vacuum
• E_ins — the electric field inside an insulator
• ΔV_ins — the potential difference inside the insulator

Some things to notice:

• When K = 1, the model behaves like a vacuum.
• When K increases: E_ins becomes smaller, V_ins becomes smaller, the arrows shrink

This is exactly what an insulator does, it reduces the electric field and potential difference inside it.

To interact with this model, press "K" to increase the dielectric constant, and "k" to decrease the dielectric constant.

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

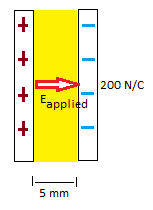
A capacitor is known to create a uniform electric field of magnitude 200 N/C. The capacitor plates are 5mm apart. A plastic slab (whose dielectric constant is 5) is carefully inserted into the gap between the capacitor. Calculate the potential difference across the insulator.

Solution

Step 1: Find [math]\displaystyle{ \Delta{V}_{vacuum} }[/math]

[math]\displaystyle{ \Delta{V}_{vacuum} = E●\vec{dl} }[/math]

[math]\displaystyle{ \Delta{V}_{vacuum} = 200*\frac{5}{1000} }[/math]

[math]\displaystyle{ \Delta{V}_{vacuum} = 1 V }[/math]

Step 2: Use the potential difference in a vacuum and the dielectric constant to find the potential difference in the insulator.

[math]\displaystyle{ \Delta{V}_{insulator} = \frac{\Delta{V}_{vacuum}}{K} }[/math]

[math]\displaystyle{ \Delta{V}_{insulator} = \frac{1}{5} }[/math]

[math]\displaystyle{ \Delta{V}_{insulator} = 0.2V }[/math]

The potential difference inside the plastic slab is 0.2 V.

Middling

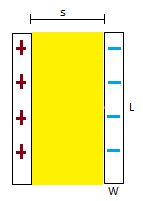
A capacitor's left plate has charge +Q. It's right plate has charge -Q. As shown in the diagram, the plates are separated by a distance s. Both plates have a length L and a width W. An insulator with dielectric constant K is inserted into the gap. Find the potential difference across the capacitor.

Solution

Step 1: Find the electric field of the capacitor.

[math]\displaystyle{ {E}_{capacitor} = \frac{Q/A}{\epsilon_0 } }[/math]

[math]\displaystyle{ {E}_{capacitor} = \frac{Q/LW}{\epsilon_0 } }[/math]

Step 2: Find the potential difference across the capacitor if there was no insulator.

[math]\displaystyle{ \Delta{V}_{vacuum} = E●\vec{dl} }[/math]

[math]\displaystyle{ \Delta{V} = \frac{Q/LW}{\epsilon_0}*s }[/math]

Step 3: Use the dielectric constant to find the potential difference across the insulator.

[math]\displaystyle{ \Delta{V}_{insulator} = \frac{\Delta{V}_{vacuum}}{K} }[/math]

[math]\displaystyle{ \Delta{V}_{insulator} = \frac{Q/LW}{\epsilon_0}*\frac{s}{K} = \frac{Qs}{LWK\epsilon_0} }[/math]

Difficult

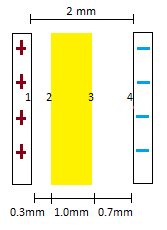
A capacitor originally has a potential difference of 500V. The capacitor plates are 2mm apart. A 1mm thick plastic slab (whose dielectric constant is 5) is inserted into the gap between the capacitor, but it does not fill the gap. It is placed 0.3mm from the positively charged left plate and 0.7mm from the negatively charged left plate. Calculate the following potential differences: [math]\displaystyle{ {V}_{1}-{V}_{2} }[/math], [math]\displaystyle{ {V}_{2}-{V}_{3} }[/math], [math]\displaystyle{ {V}_{3}-{V}_{4} }[/math], and [math]\displaystyle{ {V}_{1}-{V}_{4} }[/math].

Solution

Step 1: Find [math]\displaystyle{ {V}_{1}-{V}_{2} }[/math]

Originally, the potential difference in the capacitor is 500V. We must solve for the electric field in the capacitor (without the insulator) first. [math]\displaystyle{ E = \frac{\Delta{V}}{\vec{dl}} = \frac{500}{0.002} = 250000 N/C }[/math]

Because the insulator is not present in the area between points 1 and 2, we can find the potential difference from point 1 to point 2 by multiplying the electric field by the distance between points.

[math]\displaystyle{ \Delta{V} = E●\vec{dl} }[/math]

[math]\displaystyle{ {V}_{1}-{V}_{2} = 250000*.0003 = 75V }[/math]

Step 2: Find [math]\displaystyle{ {V}_{2}-{V}_{3} }[/math] In order to find this quantity, we must first find the potential difference that would occur in a vacuum. To do this, we take the electric field we found in step 1 and multiply by the distance.

[math]\displaystyle{ \Delta{V} = E●\vec{dl} }[/math]

[math]\displaystyle{ \Delta{V} = 250000*.001 = 250V }[/math]

Next, we must use the dielectric constant of plastic to find the potential difference in the insulator.

[math]\displaystyle{ \Delta{V}_{insulator} = \frac{\Delta{V}_{vacuum}}{K} }[/math]

[math]\displaystyle{ {V}_{2}-{V}_{3} = \frac{250}{5} = 50V }[/math]

Step 3: Find [math]\displaystyle{ {V}_{3}-{V}_{4} }[/math]

Because the insulator is not present in the area between points 3 and 4, we can find the potential difference from point 3 to point 4 by multiplying the electric field by the distance between points.

[math]\displaystyle{ {V}_{3}-{V}_{4} = E●\vec{dl} = 250000*0.007 = 175V }[/math]

Step 4: Find [math]\displaystyle{ {V}_{1}-{V}_{4} }[/math]

In order to find the potential difference between points 1 and 4, we simply need to add up the potential differences found in steps 1-3.

[math]\displaystyle{ {V}_{1}-{V}_{4} = 75V + 50V + 175V = 300V }[/math]

Connectedness

Understanding insulation is particularly important in fully comprehending circuits and electricity. Although not used as commonly in experimental entry-level physics (such as Physics 2211 or 2212) as elements of circuits like capacitors and resistors, insulators have a more practical application. As evidenced by several of the examples on this page, the potential difference across an insulator is always significantly less than through a vacuum. Because they do not let electric charge flow easily from one atom to another, insulators are used to coat wires in order to protect human users from the dangerously high voltage produced by some electric current.

History

Potential difference is a phenomenon that was first discovered by Alessandro Volta, an Italian physicist who lived from 1745 to 1827. Through his work with Luigi Galvani, Volta detected the flow of electric current through various conducting materials. This led to the discovery of electromotive force (what we more commonly refer to as emf) and eventually allowed Volta to create the first battery. Slightly later, German physicist Georg Ohm began studying Volta's research. Through experimentation, Ohm was the first to uncover the relationship between the potential difference applied through a conductor and the resultant electric current. These scientists and their findings were crucial to discovering the relationships between current, resistance, electric field, and voltage/potential difference.

See also

Further Reading

In order to more fully understand potential difference in an insulator, a basic understanding of potential difference through a vacuum is necessary. These other Physics Book Wiki pages should further one's understanding of this topic.

• Potential Difference in a Uniform Field

• Potential Difference Path Independence

• Sign of Potential Difference

External links

• https://www.youtube.com/watch?v=TFGpgfe3Q2g

• http://physics.bu.edu/~duffy/semester2/c08_dielectric.html

References

• http://www.physics.sjsu.edu/becker/physics51/capacitors.htm
• https://www.nde-ed.org/EducationResources/HighSchool/Electricity/conductorsinsulators.htm
• http://www.physics.utah.edu/~woolf/2220_buehler/electricpotential.pdf
• Matter and Interactions, 4th Edition by: Ruth Chabay and Bruce Sherwood

-cbrogan7