Potential Difference Path Independence: Difference between revisions
No edit summary |
|||
| (6 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
By: Amanda L | |||
The potential difference <math>\Delta V = V_B - V_A</math> between two locations A and B does not depend on the path taken between the locations. | The potential difference <math>\Delta V = V_B - V_A</math> between two locations A and B does not depend on the path taken between the locations. | ||
==The Main Idea== | ==The Main Idea== | ||
| Line 75: | Line 77: | ||
<math>= \frac{1}{4 \pi \epsilon_0 }Q(\frac{1}{r_2} - \frac{1}{r_1})</math> | <math>= \frac{1}{4 \pi \epsilon_0 }Q(\frac{1}{r_2} - \frac{1}{r_1})</math> | ||
=== | ===Round Trip Potential Difference=== | ||
Since the only points that matter when calculating the potential difference are the initial and final locations, then the round trip potential of any path will equal <math>0</math> since the initial and final locations are the same. | |||
Take for example this very simple circuit: | |||
[[File:circuit.png|thumb|none|alt=Potential Difference Path Independence|Simple Circuit]] | |||
The potential produced by the battery is equivalent to its <math>emf</math>. | |||
== | Since circuits obey the conservation of energy the potential difference across the whole circuit must equal <math>0</math> | ||
Therefore: | |||
<math>\Delta V = V_b + V_w = emf + (-EL) = 0</math> | |||
== See also == | == See also == | ||
Electric Field of a Point Charge | |||
Electric Field of a Capacitor | |||
Potential Difference in a Uniform Field | |||
Potential Difference of a point charge in a non-Uniform Field | |||
===External links=== | ===External links=== | ||
http://www.physicsclassroom.com/class/circuits/Lesson-1/Electric-Potential-Difference | |||
https://en.wikipedia.org/wiki/Voltage | |||
==References== | ==References== | ||
Chabay, R., & Sherwood, B. (2015). Electric Potential. In Matter & interactions (4th ed., Vol. Two, pp. 644 - 648). Danvers, Massachusetts: J. Wiley & sons. | |||
[[Category:Which Category did you place this in?]] | [[Category:Which Category did you place this in?]] | ||
Latest revision as of 16:01, 1 December 2015
By: Amanda L
The potential difference [math]\displaystyle{ \Delta V = V_B - V_A }[/math] between two locations A and B does not depend on the path taken between the locations.
The Main Idea
The potential difference between two locations A and B does not depend on the path taken between the locations. A round trip potential difference is always zero.
Potential Difference Equations
In a uniform electric field the potential difference is equal to [math]\displaystyle{ \Delta V = -\vec{E}●\Delta \vec{l} = -(E_x●\Delta x + E_y●\Delta y + E_z●\Delta z }[/math]).
In a nonuniform electric field the potential difference is equal to [math]\displaystyle{ \textstyle\int\limits_{i}^{f}-Edl }[/math]
Examples
Simple Example of Two Different Paths
Calculate the potential difference going from A to C: [math]\displaystyle{ \Delta V = V_C - V_A = ? }[/math]
Path 1
Since the electric field inside the capacitor is uniform all along the path we can use the equation for a uniform electric field [math]\displaystyle{ \Delta V = -\vec{E}●\Delta \vec{l} = -(E_x●\Delta x + E_y●\Delta y + E_z●\Delta z }[/math])
The displacement vector: [math]\displaystyle{ \Delta l = \lt \Delta x, \Delta y, \Delta z\gt = \lt (x_1 - 0),(-y_1 - 0)\gt = \lt (x_1,-y_1)\gt }[/math]
The electric field vector is given as: [math]\displaystyle{ \vec{E} = \lt (E_x,0,0)\gt }[/math]
Therefore the potential difference between A and C is: [math]\displaystyle{ \Delta V = -\vec{E}●\Delta \vec{l} = -E_x(x_1) + 0(-y_1) + 0(0) = -E_xx_1 }[/math]
Path 2
Along the path from A to B:
The displacement vector: [math]\displaystyle{ \Delta l = \lt \Delta x, \Delta y, \Delta z\gt = \lt (x_1 - 0),(0 - 0)\gt = \lt (x_1,0)\gt }[/math]
The potential difference between A and B is: [math]\displaystyle{ V_B - V_A = -\vec{E}●\Delta \vec{l} = -E_x(x_1) + 0(0) + 0(0) = -E_xx_1 }[/math]
Along the path from B to C:
The displacement vector: [math]\displaystyle{ \Delta l = \lt \Delta x, \Delta y, \Delta z\gt = \lt (x_1 - x_1),(0 - y_1)\gt = \lt (0,-y_1)\gt }[/math]
The potential difference between B and C is: [math]\displaystyle{ V_C - V_B = -\vec{E}●\Delta \vec{l} = -E_x(0) + 0(-y_1) + 0(0) = 0 }[/math]
Therefore the potential difference from A to C is: [math]\displaystyle{ \Delta V = (V_B - V_A) + (V_C - V_B) = -E_xx_1 + 0 = -E_xx_1 }[/math]
Two Different Paths Near a Point Charge
Along a straight path from a point charge Q we know that [math]\displaystyle{ \Delta V = \frac{1}{4 \pi \epsilon_0 }Q(\frac{1}{r_2} - \frac{1}{r_1}) }[/math]
Path 2
From the initial point [math]\displaystyle{ i }[/math] to point [math]\displaystyle{ A }[/math], [math]\displaystyle{ \vec{E} }[/math] is perpendicular to [math]\displaystyle{ \Delta l }[/math] so [math]\displaystyle{ \Delta V_1 = 0 }[/math]
From [math]\displaystyle{ A }[/math] to [math]\displaystyle{ B }[/math]: [math]\displaystyle{ \Delta V_2 = \frac{1}{4 \pi \epsilon_0 }Q(\frac{1}{r_3} - \frac{1}{r_1}) }[/math]
From [math]\displaystyle{ B }[/math] to [math]\displaystyle{ C }[/math]: [math]\displaystyle{ \Delta V_3 = 0 }[/math], since [math]\displaystyle{ \vec{E} }[/math] is perpendicular to [math]\displaystyle{ \Delta l }[/math].
From C to [math]\displaystyle{ f }[/math]: [math]\displaystyle{ \Delta V_4 = \frac{1}{4 \pi \epsilon_0 }Q(\frac{1}{r_2} - \frac{1}{r_3}) }[/math]
To find [math]\displaystyle{ V_f - V_i }[/math] add up all the [math]\displaystyle{ \Delta V's }[/math]
[math]\displaystyle{ V_f - V_i = \Delta V_1 + \Delta V_2 + \Delta V_3 + \Delta V_4 }[/math]
[math]\displaystyle{ = 0 + \frac{1}{4 \pi \epsilon_0 }Q(\frac{1}{r_3} - \frac{1}{r_1}) + 0 + \frac{1}{4 \pi \epsilon_0 }Q(\frac{1}{r_2} - \frac{1}{r_3}) }[/math]
[math]\displaystyle{ = \frac{1}{4 \pi \epsilon_0 }Q(\frac{1}{r_2} - \frac{1}{r_1}) }[/math]
Round Trip Potential Difference
Since the only points that matter when calculating the potential difference are the initial and final locations, then the round trip potential of any path will equal [math]\displaystyle{ 0 }[/math] since the initial and final locations are the same.
Take for example this very simple circuit:
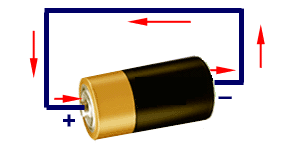
The potential produced by the battery is equivalent to its [math]\displaystyle{ emf }[/math].
Since circuits obey the conservation of energy the potential difference across the whole circuit must equal [math]\displaystyle{ 0 }[/math]
Therefore: [math]\displaystyle{ \Delta V = V_b + V_w = emf + (-EL) = 0 }[/math]
See also
Electric Field of a Point Charge
Electric Field of a Capacitor
Potential Difference in a Uniform Field
Potential Difference of a point charge in a non-Uniform Field
External links
http://www.physicsclassroom.com/class/circuits/Lesson-1/Electric-Potential-Difference
https://en.wikipedia.org/wiki/Voltage
References
Chabay, R., & Sherwood, B. (2015). Electric Potential. In Matter & interactions (4th ed., Vol. Two, pp. 644 - 648). Danvers, Massachusetts: J. Wiley & sons.